Bonjour!
Je vais entrer en terminale S et rencontre dans de plus en plus de cours sur Internet ou d'exercices l'utilisation du sigma qui m'est totalement étranger. Je sais que ça correspond à une sommation mais je ne comprends pas ce qu'il signifie et ce qu'il donne au final.
Connaitriez vous un cours que je pourrais trouver sur l'utilisation du sigma, à quoi il correspond, ou pouvez-vous me donner des exemples concrets qui pourraient me réconcilier avec ce fameux sigma et rendre la compréhension de mes cours plus simple ?
Merci d'avance pour votre aide et merci aussi du temps que vous m'accordez.
Cordialement,
Eponah.
Problèmes d'utilisation du sigma.
4 messages
- Page 1 sur 1
Eponah a écrit:Bonjour!
Je vais entrer en terminale S et rencontre dans de plus en plus de cours sur Internet ou d'exercices l'utilisation du sigma qui m'est totalement étranger. Je sais que ça correspond à une sommation mais je ne comprends pas ce qu'il signifie et ce qu'il donne au final.
Connaitriez vous un cours que je pourrais trouver sur l'utilisation du sigma, à quoi il correspond, ou pouvez-vous me donner des exemples concrets qui pourraient me réconcilier avec ce fameux sigma et rendre la compréhension de mes cours plus simple ?
Merci d'avance pour votre aide et merci aussi du temps que vous m'accordez.
Cordialement,
Eponah.
Bonjour,
Tu peux déjà aller jeter un oeil sur la page wiki correspondante http://fr.wikipedia.org/wiki/Symbole_somme
En fait, le symbole sigma est utilisé pour ne pas avoir à écrire toute une somme de termes qui peut s'avérer très longue. Par exemple, lorsqu'on écrit
Donc si l'on décompose la somme on obtient:
k est appelé l'indice de sommation. Son importance est capitale car pour réunir une addition de termes sous un unique signe Sigma, il faut que tous ces termes aient quelque chose "en commun". Disons qu'on ne peut pas réunir sous un signe Sigma une addition de nombres pris totalement au hasard, c'est pour cela qu'on ne peut mettre sous le signe Sigma que la somme d'une famille de termes.
Prenons un petit exemple. Imaginons que l'on veuille écrire la somme de tous les entiers naturels entre 0 et 100. Intuitivement on écrit 0+1+2+3+...+100. Si l'on reprend l'expression développée de Sigma que j'ai donnée tout-à-l'heure, on sait que l'on peut écrire cette somme sous la forme
0+1+2+3+...+100=
Maintenant, il reste à trouver le terme général de la somme, soit le
Donc en faisant la somme des
Reste à écrire ça sous forme d'un sigma en identifiant chaque terme:
Ici, n=100 et
Je vais essayer de te dégotter un cours clair là-dessus.
Pour compléter la réponse de Peacekeeper, je rajouterais que l'on somme des termes indexés (genre les termes d'une suite particulière) ou des termes dépendants d'une variable entière que l'on nomme k, par exemple.
Ainsi, sommer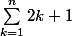 revient à faire la somme des termes de la forme 2k+1, pour k allant de 1 à n.
revient à faire la somme des termes de la forme 2k+1, pour k allant de 1 à n.
Pour calculer ce truc, on casse la sommation :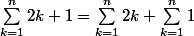
Or la somme des 1 de k=1 à n ça fait n (parce qu'on additionne n fois 1).
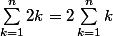 par factorisation. Or on sait que
par factorisation. Or on sait que }{2}) donc
donc ) .
.
D'où finalement+n=n(n+2)) .
.
Ainsi, sommer
Pour calculer ce truc, on casse la sommation :
Or la somme des 1 de k=1 à n ça fait n (parce qu'on additionne n fois 1).
D'où finalement
Un petit cours synthétique sur les sommes (et les produits en passant) qui expose synthétiquement les techniques d'utilisation de cette notation et les règles de calcul associées. :happy3:
J'espère que ça te sera utile!
Cordialement,
Peacekeeper
http://ljk.imag.fr/membres/Bernard.Ycart/mel/ca/node3.html
J'espère que ça te sera utile!
Cordialement,
Peacekeeper
http://ljk.imag.fr/membres/Bernard.Ycart/mel/ca/node3.html
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
