Je veux résoudre dans
Si
Or
Par suite, il vient :
D'où S={
Dinozzo13 a écrit:Bonsoir, j'aimerais savoir si mon raisonnement est correct, merci d'avance ^^.
Je veux résoudre dans:
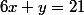
.
donc une solution particulière de
est
, car
x
.
Sidésigne une solution générale de
alors on a :
.
Or, donc
divise
.
tel que
.
Par suite, il vient :.
D'où S={}
Dinozzo13 a écrit:Dites-moi, comme en ce moment c'est "arithmétique", je me demandais où trouver des exercices sur les congruences et sur les équation diophantiennes mais avec des entiers complexes, c'est-à-dire dans, parce que je commence à me lasser des entiers, je voudrais bien aller plus loin.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :