Introduire des entiers complexes : 1°) dans les équations di
Ce serait un peu long... Je me suis mal exprimé. Ce que je voulais dire c'est que quand tu calcules un pgcd, tu peux multiplier par un inversible (en l'occurence 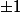 ou
ou 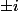 ), ce que tu trouves restera vrai. Il y a en fait un abus de notation avec
), ce que tu trouves restera vrai. Il y a en fait un abus de notation avec 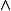 qui est que le résultat n'est pas unique. Donc trouver un (noter le "un", encore!) pgcd égal à
qui est que le résultat n'est pas unique. Donc trouver un (noter le "un", encore!) pgcd égal à  ou à
ou à  revient rigoureusement au même.
revient rigoureusement au même.
Si ça t'intéresse jette un oeil sur Wikipédia pour les relations d'équivalence. Ce que je voulais dire c'était que le pgcd est en fait une classe d'équivalence modulo les inversibles.
Si ça t'intéresse jette un oeil sur Wikipédia pour les relations d'équivalence. Ce que je voulais dire c'était que le pgcd est en fait une classe d'équivalence modulo les inversibles.
skilveg a écrit:Ce serait un peu long... Je me suis mal exprimé. Ce que je voulais dire c'est que quand tu calcules un pgcd, tu peux multiplier par un inversible (en l'occurenceou
), ce que tu trouves restera vrai. Il y a en fait un abus de notation avec
qui est que le résultat n'est pas unique. Donc trouver un (noter le "un", encore!) pgcd égal à
ou à
revient rigoureusement au même.
OK.
Mais pourquoi alors on me dit que
Voilà ce que j'ai écrit :
j'étudie\wedge{(4-i)}) .
.
Soit tel que
tel que 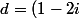\wedge{(4-i)}) ;
;  divise
divise 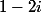 et
et 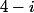 .
.
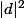 divise
divise 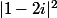 et
et 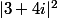 .
.
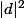 divise donc 5 et 25.
divise donc 5 et 25.
Je pose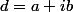 avec
avec \in\mathbb{Z}^{2}) .
.
Par suite, il vient :
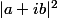 divise 5 et 25 donc
divise 5 et 25 donc 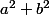 divise 5 et 25 et par conséquent
divise 5 et 25 et par conséquent 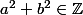 .
.
Or les diviseurs communs à 5 et 25 sont :
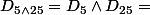 {
{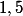 }, donc je cherche tous les couples
}, donc je cherche tous les couples ) tels que :
tels que :
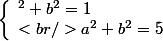 .
.
=) {
{,(\pm2,\pm1),(0,\pm1),(\pm1,0)) }.
}.
Donc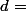 {
{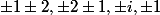 }.
}.
Mais après, je ne sais pas quoi faire, pourriez-vous m'aider ?
j'étudie
Soit
Je pose
Par suite, il vient :
Or les diviseurs communs à 5 et 25 sont :
Donc
Mais après, je ne sais pas quoi faire, pourriez-vous m'aider ?
Dinozzo13 a écrit:Voilà ce que j'ai écrit :
j'étudie.
Soittel que
;
divise
et
.
divise
et
.
divise donc 5 et 25.
Je poseavec
.
Par suite, il vient :divise 5 et 25 donc
divise 5 et 25 et par conséquent
.
Or les diviseurs communs à 5 et 25 sont :{
}, donc je cherche tous les couples
tels que :
.
{
}.
Donc{
}.
Mais après, je ne sais pas quoi faire, pourriez-vous m'aider ?
Je ne sais pas si j'ai tort ou non mais je pense que
n'a pas de solutions...
EDIT : Attention tout de même. Si (a,b) est solution de ce système d'équations, c'est que (a,b) vérifie les deux équations en même temps. Là, j'ai compris en relisant bien ton message que tu veux que (a,b) vérifie l'une des deux équations. Ce n'est donc pas la bonne notation qu'il faut employer...
Regroupe ceux qui sont égaux à un facteur indivisible près. Cela te donnera "un certain nombre" (jlai pas fait je sais pas) de "d" possibles. Tu fait une étude de cas (sont-ils tous des diviseurs communs ?) et en fonction de cela, tu regarde quel est le plus grand selon le critère de divisibilité. Tu peux ensuite conclure sur le pgcd.
Exact. Attention à la notation.
Clembou a écrit:Je ne sais pas si j'ai tort ou non mais je pense que
n'a pas de solutions...
EDIT : Attention tout de même. Si (a,b) est solution de ce système d'équations, c'est que (a,b) vérifie les deux équations en même temps. Là, j'ai compris en relisant bien ton message que tu veux que (a,b) vérifie l'une des deux équations. Ce n'est donc pas la bonne notation qu'il faut employer...
Exact. Attention à la notation.
Clembou a écrit:EDIT : Attention tout de même. Si (a,b) est solution de ce système d'équations, c'est que (a,b) vérifie les deux équations en même temps. Là, j'ai compris en relisant bien ton message que tu veux que (a,b) vérifie l'une des deux équations. Ce n'est donc pas la bonne notation qu'il faut employer...
oui oui ^^ il n'y a pas d'accolade ^^
Djmaxgamer a écrit:Regroupe ceux qui sont égaux à un facteur indivisible près. Cela te donnera "un certain nombre" (jlai pas fait je sais pas) de "d" possibles. Tu fait une étude de cas (sont-ils tous des diviseurs communs ?) et en fonction de cela, tu regarde quel est le plus grand selon le critère de divisibilité.
Euh, je ne vois pas bien, pourrais-tu m'éclairer un peu plus ?
Dinozzo13 a écrit:Euh, je ne vois pas bien, pourrais-tu m'éclairer un peu plus ?
Reprenons l'exemple que nous avions fait :
Djmaxgamer a écrit:Le voilà, correct, avec quelques annotations en couleur :
Soit d=pgcd(5+5i, 3+4i)
d divise 5+5i et 3+4i (normal ^^)
|d|^2 divise |5+5i|^2 et |3+4i|^2 (normal encore)
|d|^2 divise 50 et 25 (tu calcule les modules au carré)
En posant : d=a+ib avec (a,b) dans Z on a, en remplacant :
|a+ib|^2 divise 50 et 25
a^2+b^2 divise 50 et 25 (le module au carré d'un complexe a+ib est a^2+b^2)
(a^2+b^2) est dans Z (puisque le module d'un complexe élevé au carré est dans Z (et aussi car a et b sont dans Z))
Les diviseurs communs à 50 et 25, sont, dans Z {1,5,25} pas besoin d'expliquer ça normalement :p
Le couple (a,b) peut donc être, car a^2+b^2 peut être égal à 1, 5 ou 25 (diviseurs communs de 50 et 25) un pitit raisonnement logique donne ces possibilités pour a et b :
d peut être alors, comme d=a+ib :
La tu t'es arreté
En regroupant les regroupant en égaux à un facteur inversible près normalement tu as compris non ? Ceux qui sont égaux si multipliés par i, -i, 1 ou -1. Du point de vue des PGCD : PGCD(x,y)=x=-x (Dans Z) dans Z les facteurs inversibles sont 1 et -1 seulement. Donc dans Z[i] on a : PGCD(x,y)=x=-x=xi=-xi Ici le travail consiste à regrouper ces valeurs. Ensuite, si x est PGCD alors -x,xi et -xi le sont. On restreint donc les possibilités :
De ce fait, il suffit de restreindre la recherche à
pgcd(5+5i, 3+4i) = 1 ou 1+2i ou 1-2i ou 3+4i ou 3-4i vu que les autres pgcd possibles sont égaux à un facteur inversible près. On passe donc d'un grand nombre de valeurs possibles à uniquement 5.
Ensuite tu fais une étude de cas : parmi ces 5 valeurs possibles de d, lesquels sont diviseurs communs. On a vu les valeurs vérifiant |d|^2=... mais cela n'assure pas que d divise 3+4i et 5+5i (les deux nombres dont on veux connaitre le PGCD). Il faut donc le vérifier. Pour cela, on pose les fractions dans C et on regarde si le résultat est un entier de Gauss (donc qu'il y a divisibilité) ou pas (dans ce cas le nombre ne peut pas être un diviseur commun). Bien entendu, si le nombre est diviseur commun, il faut le vérifier pour les deux nombres (COMMUN) parce que si une valeur possible de d divise un des deux nombre, cela n'implique pas qu'elle divise l'autre. Par contre, un seul contre-exemple suffit (pour montrer que ce n'est pas un diviseur commun il faut et il suffit de montrer qu'il ne divise pas un des nombres).
Puisque
Commeon a
et donc 1+2i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 3+4i.
De plus :
Commeon a
et donc 3+4i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 5+5i.
Et encore :
Commeon a
et donc 3-4i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 3+4i.
Et encore :
Commeon a
donc 1-2i divise 3+4i
De même :
Commeon a
donc 1-2i divise 5+5i
1-2i est un diviseur commun à (3+4i) et (5+5i)
Rappel de la définition du PGCD : Plus GRAND Commun Diviseur. Une fois qu'on a toutes les valeurs possibles (c'est à dire vérifiant |d|^2=... ET étant diviseur commun) il faut choisir la plus grande. Dans Z[i] on ne peut pas parler strictement de "plus grande" (pas de notion de grandeur avec les complexes !) MAIS on peut parler de grandeur du point de vue de la divisibilité. De ce point de vu, le plus grand des nombres (le pgcd) est un multiple de tous les autres.
De plus, 1-2i est multiple de 1, donc 1-2i est plus grand au niveau de la divisibilité que 1. C'est ce qu'on applique ici : 1 divise 1-2i (bien entendu ^^) donc 1-2i est un multiple de toutes les autres valeurs possibles du PGCD. C'est don c le plus grand du point de vue de la divisibilité.
Dans ce cas :
pgcd(5+5i, 3+4i) = 1-2i
Mais pour reprendre la classification de nombre égaux à un facteur inversible près, on a :
pgcd(5+5i, 3+4i) = \{1-2i,-2-i,-1+2i,2+i\} (je ne sais pas si on peut noter comme ça)
C'est plus clair ?
Djmaxgamer a écrit:C'est plus clair ?
Oui merci, je vois mieux sous forme de résumé plutôt qu'en morceaux un peu dispersés dans toutes ces pages ^^.
J'ai regardé tout ce que nous avons fait ensemble, et j'ai remarqué que, jusque là, nous n'avions résolu que des équations diophantiennes de la forme ax+by=c avec a,b et c entiers de Gauss ^^. Mais, je me suis demandé, comment ferait-on si l'on avait une équation de la forme ax+by=cxy, avec, évidemment, a,b et c entiers de Gauss :bad:.
PS: Si j'ai des questions sur ton résumé, j'espère que tu seras là pour y répondre ^^.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
