Introduire des entiers complexes : 1°) dans les équations di

par **Dinozzo13** » 15 Juil 2009, 17:36

Non non, je ne veux pas parler de l'équation en particulier, je veux parler de ce genre d'équations ax+by=c avec a,b et c entiers de Gauss en général.

par **leon1789** » 15 Juil 2009, 17:39

Dinozzo13 a écrit:Non non, je ne veux pas parler de l'équation en particulier, je veux parler de ce genre d'équations ax+by=c avec a,b et c entiers de Gauss en général.

Hé bien, cette équation possède des solutions si et seulement si pgcd(a,b) divise c.
Si tel est le cas, alors les solutions sont de la forme (x_o, y_o) + solutions de l'équation ax+by=0.

par **Djmaxgamer** » 15 Juil 2009, 17:43

leon1789 a écrit:Voilà, c'est pas très compliqué : on multiplie l'équation initiale par 1+i de chaque coté, il vient alors , ou encore

Est-ce que appartient à Z[i] ?
A vous de conclure.

Oui c'est un cas simple. J'ai changé l'équation et essayé de résoudre (qu'il y ai des solutions) et ça ne marche pas (je peux te recopier ma tentative, c'était pour (1+i)x+(1-i)y=4+2i qui équivaut à 2(ix+y)=2+6i qui a donc des solutions. J'avais essayé de refaire avec ma méthode (xi, xr et tout) mais pas possible de résoudre. Et ici, la simplification est simple (pour vérifier si il y a des solutions dans Z[i]) j'ai pas réussi par exemple pour plus compliqué comme : (3-5i)x+(2+3i)y=1+i.

J'aimerais donc (on aimerais) disons une manière formelle, de résoudre ces équations dans Z[i] (dans le cas général : autant vérifier si il y a des solutions que les trouver).

Si tu veux illustre cette formalisation avec l'exemple ci dessus, à savoir (3-5i)x+(2+3i)y=1+i (libre à toi de changer le "1+i" pour que l'équation ait des solutions)

par **Dinozzo13** » 15 Juil 2009, 17:50

Djmaxgamer a écrit:Oui c'est un cas simple. J'ai changé l'équation et essayé de résoudre (qu'il y ai des solutions) et ça ne marche pas (je peux te recopier ma tentative, c'était pour (1+i)x+(1-i)y=4+2i qui équivaut à 2(ix+y)=2+6i qui a donc des solutions. J'avais essayé de refaire avec ma méthode (xi, xr et tout) mais pas possible de résoudre. Et ici, la simplification est simple (pour vérifier si il y a des solutions dans Z[i]) j'ai pas réussi par exemple pour plus compliqué comme : (3-5i)x+(2+3i)y=1+i.

J'aimerais donc (on aimerais) disons une manière formelle, de résoudre ces équations dans Z[i] (dans le cas général : autant vérifier si il y a des solutions que les trouver).

Si tu veux illustre cette formalisation avec l'exemple ci dessus, à savoir (3-5i)x+(2+3i)y=1+i (libre à toi de changer le "1+i" pour que l'équation ait des solutions)

oui, comme tu le dis c'est un cas simple et précis, je pense qu'on aimerais bien savoir résoudre n'importe laquelle de ces equations avec des entiers de Gauss, c'est pour ça que j'aurais aimé que vous nous rédigiez une méthode précise et efficace ^^

par **Djmaxgamer** » 15 Juil 2009, 18:10

Pas forcement une méthode, mais des conseils de méthodes en tous cas pour des personnes n'ayant pas pour habitudes de manipuler des entiers de gauss ^^

Je pense que si vous ne voulez pas vous embêter, un petit lien intéressant sur un cours ou autre peut suffire (car je pense que savoir juste résoudre ces équations, même si c'est intéressant, c'est mieux si on comprends pour quoi (quelle lois utiliser toussa toussa)) parce qu'il faut avouer que notre demande comme ça, ça peut ne pas être de la tarte ^^

par **Dinozzo13** » 15 Juil 2009, 18:12

leon1789 a écrit:Est-ce que appartient à Z[i] ?
A vous de conclure.

Non

n'appartient pas à Z[i] donc il n'y a pas de solutions.

par **leon1789** » 15 Juil 2009, 18:32

Dinozzo13 a écrit:Non n'appartient pas à Z[i] donc il n'y a pas de solutions.

oui, exact.

Pour résoudre une équation linéaire ax+by=c dans Z[i], j'ai essayé de résumer très rapidement la situation dans le message #82.

par **Dinozzo13** » 15 Juil 2009, 18:37

Djmaxgamer a écrit:Et bien supposons qu'on ait raison, on peut essayer d'en résoudre un "simple"

(1+i)x + (1-i)y = 3+2i

Ca te dit de tester ? Au pire on trouve pas, nos erreurs sont vues et corrigées, au mieux on trouve \o/ (si on suppose qu'on a raison x) )

signifiant respectivement partie réelle et partie imaginaire de x
L'équation devient :

J'aurais essayé xD

Enfin de toutes façons avec 2 équations et 4 inconnues je pense pouvoir avoir un résultat mais j'ai jamais vraiment fait ça (en dynamique en SI un peu mais beaucoup plus simple =/ )

Je crois que c'est possible tu peux te ramener à deux équations diophantienne et trouver des couples entiers de solutions, et comme ces couples sont les parties imaginaires et complexes des complexes x et y, on peut trouver l'ensemble des solutions. Mais je pense que cette manière de faire est fastidieuse, je vais quand même essayer d'aboutir...

D'autre part,

On se retrouve donc avec deux équations diophantiennes qu'on sait résoudre dans Z

J'ai faux ?

-1 et 5 ne sont pas pairs...pas de solutions ?

Je me contredit ^^ on est dans C donc on ne doit pas résoudre ces équations diophantiennes dans Z mais dans R...plus dur déjà (donc plus intéressant ^^) (EDIT : je me re-contredit : non ce n'est pas plus dur ^^)

Explication :

YEAH j'ai mes solutions (après vérifications) !
Mais cela est-il vrai pour TOUTES les solutions ?
J'attends un chaman ^^

Les solutions serait donc, à mon avis, en posant :

Ce qui m'amène à un nouveau problème :

ps : je ne cherche pas absolument une relation entre k et k', mais une explication à la différence entre mon résultat (qui me parait correct) et celui de la TI. Je pense, comme je me fais confiance, que c'est équivalent...mais comment le prouver ? Et si ça ne l'est pas, où est mon erreur ?

De plus, le résultat de ma TI implique que k' est nul. Or si je prends k' = 1 et k=0, alors on a le couple :

Et une petite vérification montre bien que le couple est solution. Erreur de la TI ? On a bien :
!!

Je pense pouvoir me répondre à nouveau ^^ en utilisant le tout premier système d'équation, pour avoir k en fonction de k' et pouvoir par la suite exprimer le résultat en fonction d'un seul paramètre et donc pouvoir avoir le même résultat que la TI (qui je sais, n'est pas une référence mais je pourrais m'assurer de la crédibilité de mon résultat)

Ce qui ne m'avance a rien :mur: a l'aiiiide xD

Je pense honnêtement que la TI se goure xD (enfin j'espère ^^) mais je ne vois pas d'erreur dans mon raisonnement et je trouve que définir y comme étant une constante va à l'encontre de la condition initiale : y est un complexe.

Et vu qu'en plus si on remplace mon couple dans l'équation de départ, ça me donne pour tout k' et k , 3+2i
Si je remplace la formule de la TI ça marche aussi, mais je pense qu'il y a restriction de solutions, donc que c'est "partiellement vrai". Quelqu'un peut me dire la vérité vraie ?

sinon, dans le raisonnement de Djmaxgamer, quelle est la méthode ou less idées à retenir ?

par **leon1789** » 15 Juil 2009, 18:43

Prenons l'équation (3-5i)x+(2+3i)y=1+i notée (E)

Essayons de cerner le pgcd de 3-5i et 2+3i. De manière générale, l'algo d'Euclide (avec division euclidienne dans Z[i] :!:) permet de le calculer. Mais ici, on peut faire plus rapide.

Soit d un diviseur commun à 3-5i et 2+3i. Alors d divise (3-5i)(3+5i) = 3²+5²=34 et d divise (2+3i)(2-3i) = 2²+3²=13 , donc d divise pgcd(34,13)=1.
Conclusion : pgcd(3-5i, 2+3i)=1, OK ? et donc il y a des solutions à (E), OK ?

par **leon1789** » 15 Juil 2009, 18:45

Dinozzo13 a écrit:sinon, dans le raisonnement de Djmaxgamer, quelle est la méthode ou less idées à retenir ?

Ce que je (cela n'engage que moi) n'aime pas dans sa rédaction, c'est l'emploi inutile de 4 (!) inconnues

, alors que l'emploi simple de x et y suffit...

par **Dinozzo13** » 15 Juil 2009, 19:07

Ce que je (cela n'engage que moi) n'aime pas dans sa rédaction, c'est l'emploi inutile de 4 (!) inconnues , alors que l'emploi simple de x et y suffit...

Donc l'apparition des parties reelles et imaginaires ne fait que compliqué la résolution ?

leon1789 a écrit:Prenons l'équation (3-5i)x+(2+3i)y=1+i notée (E)

Essayons de cerner le pgcd de 3-5i et 2+3i. De manière générale, l'algo d'Euclide (avec division euclidienne dans Z[i] ) permet de le calculer. Mais ici, on peut faire plus rapide.

Je te suis ^^ ..., pourquoi un panneau attention ? y a-t-il des dangers ?

Soit d un diviseur commun à 3-5i et 2+3i. Alors d divise (3-5i)(3+5i) = 3²+5²=34 et d divise (2+3i)(2-3i) = 2²+3²=13

- lorsque tu dis que d divise (3-5i)(3+5i), tu fais apparaître la forme conjuguée de 3-5i ? pareil pour 2+3i, c'est 2-3i ?
- Faut-il appliquer ce raisonnement à chaque fois ou c'est exceptionnel ???

par **Dinozzo13** » 15 Juil 2009, 19:35

Prenons l'équation (3-5i)x+(2+3i)y=1+i notée (E)

Essayons de cerner le pgcd de 3-5i et 2+3i. De manière générale, l'algo d'Euclide (avec division euclidienne dans Z[i] ) permet de le calculer. Mais ici, on peut faire plus rapide.

Soit d un diviseur commun à 3-5i et 2+3i. Alors d divise (3-5i)(3+5i) = 3²+5²=34 et d divise (2+3i)(2-3i) = 2²+3²=13 , donc d divise pgcd(34,13)=1.
Conclusion : pgcd(3-5i, 2+3i)=1, OK ? et donc il y a des solutions à (E), OK ?

D'accord, mais que fait-on après ?

par **leon1789** » 15 Juil 2009, 19:45

Dinozzo13 a écrit:Donc l'apparition des parties reelles et imaginaires ne fait que compliqué la résolution ?

A mon avis, dans ce cas, oui ça multiplie par 2 le "basard ambiant".

Dinozzo13 a écrit:Je te suis ^^ ..., pourquoi un panneau attention ? y a-t-il des dangers ?

Je voulais signifier que ce n'est pas la même division que dans Z. (voir le message de skilveg, #77)

Dinozzo13 a écrit:- lorsque tu dis que d divise (3-5i)(3+5i), tu fais apparaître la forme conjuguée de 3-5i ? pareil pour 2+3i, c'est 2-3i ?

oui, histoire de retomber sur des entiers naturels.

Dinozzo13 a écrit:- Faut-il appliquer ce raisonnement à chaque fois ou c'est exceptionnel ?

Ce raisonnement n'est pas obligatoire, mais c'est une astuce (il y en a de plus fines) pour accélérer le calcul ...quand on a un peu de chance.

par **leon1789** » 15 Juil 2009, 19:48

Dinozzo13 a écrit:D'accord, mais que fait-on après ?

On cherche une solution particulière en utilisant ce qu'on vient de dire :
trouver u et v dans Z tels que 1 = 34u + 13v (Bezout)
puis en déduire une solution particulière de (E).

par **Dinozzo13** » 15 Juil 2009, 19:51

leon1789 a écrit:Ce raisonnement n'est pas obligatoire, mais c'est une astuce (il y en a de plus fines) pour accélérer le calcul ...quand on a un peu de chance.

du genre ?

par **leon1789** » 15 Juil 2009, 20:00

Dinozzo13 a écrit:du genre ?

par exemple, au lieu de dire

d divise A et B dans Z[i] => d divise dans Z[i]

on a un résultat plus fort qui est

d divise A et B dans Z[i] => divise dans Z.

par **Dinozzo13** » 15 Juil 2009, 20:11

Que représentent A et B ?

par **leon1789** » 15 Juil 2009, 20:12

Dinozzo13 a écrit:Que représentent A et B ?

des éléments de Z[i] voyons...

par **Dinozzo13** » 15 Juil 2009, 20:16

^^ c'était pour en être sûr ^^

par **Dinozzo13** » 15 Juil 2009, 20:28

Je résume pour ne pas me perdre ^^,

On cherche à résoudre l'équation (E) définie su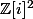r

par :
(3-5i)x+(2+3i)y=1+i (E).

Il faut regarder si (3-5i) et (2+3i) sont premiers entre eux, c-est-à-dire si

. Pour cela, on nomme d, un diviseur commun à (3-5i) et à (2+3i).
- d divise (3-5i)(3+5i)=34
- d divise (2+3i)(2-3i)=13
Donc d divise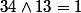

, et par conséquent

donc (E) possède des solutions dans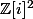

.

Ensuite, il faut chercher une solution particulière

telle que 34u+13v=1.

Jusque là, tout va bien ?
- Question: est-ce que l'ordre à une importance dans la recherche d'une solution particulière

telle que 34u+13v=1, ou 13u+34v=1 est exact aussi ?

Introduire des entiers complexes : 1°) dans les équations di

Qui est en ligne