Ca marche parce queDinozzo13 a écrit:Soit d tel que.
Introduire des entiers complexes : 1°) dans les équations di
Djmaxgamer a écrit:J'ai "demandé" à ma TI de me résoudre cette équation...elle me met :
J'ai essayé de voir si leur solution et la mienne se valent. Partons de la mienne :
Remplaçons (comme pour les équations diophantiennes "normales", essayons de voir le rapport entre k' et k (k= ??? * k' ou autre)
Bon là faut s'accrocher ^^
Or d'après mes solutions, avec
Le coupleest une solution particulière de
donc
Et donc notre relation devient :
Ce qui me donne
Ce qui ne me permet pas de conclure sur la relation entre k et k'...une autre idée ?
Alors, est-ce que ce raisonnement paraît juste ou non ?
Dinozzo13 a écrit:J'ai trouvé de nouvelles info:
En mathématiques, et plus précisément en théorie algébrique des nombres, on appelle entier de Gauss les nombres complexes dont les parties réelle et imaginaire sont des entiers relatifs, c'est-à-dire:={
}
C'est ce qu'on a pris pour résoudreavec :
Soit une équation de la forme ax + by = c où a, b et c sont des entiers de Gauss. Soit d tel que( pgcd de a et b). Alors cette équation admet des solutions dans
si, et seulement si, c est un multiple de d. Je ne sais pas si ça apporte grand chose, mais j'espère qu'au moins ce sera utile, sinon, ça enrichira notre culture ^^.
ok mais comment calculer le PGCD de deux entiers de Gauss ? Par exemple ici, quel est le pgcd de (1-i) et (1+i) ? Je dirais 1 mais comment le savoir et en être sur ? (oui, je viens dme réveiller x) )
Mais donc si je comprends bien :
Pour une résolution dans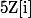 de :
de :
 : ax+by=c \text{ avec } (a,b,c) \text{ des entiers de Gauss})
il faut tout d'abord vérifier si il y a des solutions (comme tu nous l'a montré avec notre exemple), mais ensuite pour les trouver ces solutions comment procéder ?
Et d'ailleurs même dans l'exemple donné, la vérification est assez simpliste. Disons qu'avec : (34+2i)x+(23i-5)y=26+48i la je ne saurais pas du tout comment faire ^^ avant 1+i et 1-i étaient conjugués l'un de l'autre c'est plus facile déjà. Comment formaliser cette vérification ? De plus, comment trouver le PGCD de deux entiers de Gauss ?
Pour une résolution dans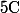 de :
de :
 : ax+by=c \text{ avec } (a,b,c) \in \mathbb{C})
Alors dans ce ca ma méthode de résolution convient-elle ? Ou il y a mieux ?
Pour une résolution dans
il faut tout d'abord vérifier si il y a des solutions (comme tu nous l'a montré avec notre exemple), mais ensuite pour les trouver ces solutions comment procéder ?
Et d'ailleurs même dans l'exemple donné, la vérification est assez simpliste. Disons qu'avec : (34+2i)x+(23i-5)y=26+48i la je ne saurais pas du tout comment faire ^^ avant 1+i et 1-i étaient conjugués l'un de l'autre c'est plus facile déjà. Comment formaliser cette vérification ? De plus, comment trouver le PGCD de deux entiers de Gauss ?
Pour une résolution dans
Alors dans ce ca ma méthode de résolution convient-elle ? Ou il y a mieux ?
Djmaxgamer a écrit: il faut tout d'abord vérifier si il y a des solutions (comme tu nous l'a montré avec notre exemple).
:doh: excuse, je ne comprends pas, se pourrait-il qu'il n y ait pas de solution ? comment cela se fait-il ?
Djmaxgamer a écrit:mais ensuite pour les trouver ces solutions comment procéder ?
Je pense qu'il faut faire comme tu l'as fait à la page 3 je crois, on distingue les parties réelles et imaginaires et on résouds un système.
Djmaxgamer a écrit:comment trouver le PGCD de deux entiers de Gauss ?
ça doit pas être dur, le seul problème, c'est le i, je sais que
Djmaxgamer a écrit:ok mais comment calculer le PGCD de deux entiers de Gauss ? Par exemple ici, quel est le pgcd de (1-i) et (1+i) ? Je dirais 1 mais comment le savoir et en être sur ?
moi aussi, j'aurais dit que
Comme il a été dit, les entiers de Gauss forment un anneau euclidien. On parle indifféremment de nombre premier de Gauss ou d'entier irréductible. Le groupe des unités contient quatre éléments {1,-1,i,-i}.
Ainsi un entier de Gauss et dit irréductible si, et seulement si toute division en deux facteurs contient une unité et qu'il n'est pas élément du groupe des unités. 3, -3, 3i et -3i sont appelés nombres premiers de Gauss. Si a et b sont deux entiers de Gauss, alors il existe quatre représentants pour le pgcd (y compris le ppmc)
Dinozzo13 a écrit::doh: excuse, je ne comprends pas, se pourrait-il qu'il n y ait pas de solution ? comment cela se fait-il ?
Parce qu'on résout dans
J'avais résolu dans
Djmaxgamer a écrit:
-1 et 5 ne sont pas pairs...pas de solutions ?
et donc pas de solutions dans Z[i].
Ou encore :
leon1789 a écrit:On multiplie par 1+i de chaque coté (E)
Est-ce que 5i-1 est multiple de 2 dans Z[i] ?
A vous de conclure.
Je te renvoie d'ailleurs à ton propre post ^^
Dinozzo13 a écrit:J'ai trouvé de nouvelles info:
En mathématiques, et plus précisément en théorie algébrique des nombres, on appelle entier de Gauss les nombres complexes dont les parties réelle et imaginaire sont des entiers relatifs,[...]
Soit une équation de la forme ax + by = c où a, b et c sont des entiers de Gauss. Soit d tel que( pgcd de a et b). Alors cette équation admet des solutions dans
si, et seulement si, c est un multiple de d. Je ne sais pas si ça apporte grand chose, mais j'espère qu'au moins ce sera utile, sinon, ça enrichira notre culture ^^.
Donc si c n'est pas un multiple de d, l'équation n'admet pas de solution dans
Dinozzo13 a écrit:Je pense qu'il faut faire comme tu l'as fait à la page 3 je crois, on distingue les parties réelles et imaginaires et on résouds un système.
Cette manière de faire convient parfaitement pour une résolution dans
Mais pour une résolution dans
Dinozzo13 a écrit:ça doit pas être dur, le seul problème, c'est le i, je sais queou que l
l=1, mais je ne pense pas que ça serve à grand chose. :triste:
Ou bien c'est tout le problème justement xD et aussi (et surtout) que le nombre complexe est en deux partie : l'imaginaire et la réelle. Enfin bref attendons une réponse ^^
Petite remarque:dans Z[i],il y a 4 inversibles(=diviseurs de 1) qui sont 1,-1,i,-i. (alors dans Z les inversibles sont 1 et -1).Pourquoi je parle de ca?Car le pgcd est défini "a un inversible pres".Par exemple,dans Z le pgcd -4 et 6 on dit que c est 2,mais on peut aussi dire que c est -2.Par convention on choisit 2 car il est positif,mais dans les entiers de Gauss,cette convention n a plus lieu d etre .Donc si d est le pgcd de 2 entiers de Gauss a et b,-d,id et -id sont aussi pgcd de a et b.On peut dire que les nombres d,-d,id,-id sont presque egaux,dans le sens ou ils ont meme diviseurs,meme multiples...Donc dans l exemple a=1+i,b=1-i,on a b=-i*a,donc c est comme si on avait a=b:un pgcd de 1+i et 1-i,c est par exemple 1+i..
Dans le cas général,il existe probablement un algo d euclide pour calculer un pgcd,mais je ne le connais pas.Faudrait essentiellement savoir comment effectuer une division euclidienne dans Z[i].
Dans le cas général,il existe probablement un algo d euclide pour calculer un pgcd,mais je ne le connais pas.Faudrait essentiellement savoir comment effectuer une division euclidienne dans Z[i].
Djmaxgamer a écrit:Pour une résolution dansde :
Alors dans ce ca ma méthode de résolution convient-elle ? Ou il y a mieux ?
Résoudre cela dans C est immédiat (équation de degré 1 !) :
si
si
si
si
Cela est valable pour tout corps, par uniquement C...
ffpower a écrit:Dans le cas général,il existe probablement un algo d euclide pour calculer un pgcd,mais je ne le connais pas.Faudrait essentiellement savoir comment effectuer une division euclidienne dans Z[i].
C'est quasiment la même chose que dans Z :
pour tout
(:!: il n'y a pas unicité du couple (q,r) )
Effectivement, avec cette "division euclidienne", on singe complètement l'algo d'Euclide sur Z[i].
leon1789 a écrit:C'est quasiment la même chose que dans Z :
pour toutoù
, il existe
tels que a = bq+r avec |r|<|b|.
(:!: il n'y a pas unicité du couple (q,r) )
Effectivement, avec cette "division euclidienne", on singe complètement l'algo d'Euclide sur Z[i].
oui,ca je le savais,mais la question est comment on effectue cette division dans la pratique.Car d habitude pour prouver cette assertion il me semble que l on passe par des inf de certaines quantités,ce qui n est pas extraordianairement constructif..
Pour la division euclidienne, on peut la faire comme ça: le stathme sur 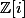 est le module. Si on a
est le module. Si on a  et
et  dans
dans 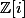 avec
avec 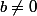 , on sait que
, on sait que 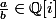 est approché par un entier de Gauss avec une différence de module inférieure à
est approché par un entier de Gauss avec une différence de module inférieure à 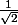 (faire un dessin de la grille représentant
(faire un dessin de la grille représentant 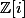 , la distance maximale à
, la distance maximale à 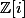 est atteinte au centre d'un carré). En arrondissant à l'entier le plus proche les parties entières de la partie réelle et de la partie imaginaire de
est atteinte au centre d'un carré). En arrondissant à l'entier le plus proche les parties entières de la partie réelle et de la partie imaginaire de 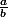 , on écrit donc
, on écrit donc 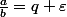 avec
avec 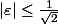 , donc
, donc 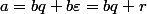 avec
avec 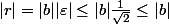 .
.
On passe bien par un inf (la distance de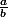 à
à 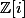 ) mais on peut le calculer de manière effective.
) mais on peut le calculer de manière effective.
Remarque: ce procédé marche encore pour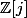 .
.
On passe bien par un inf (la distance de
Remarque: ce procédé marche encore pour
Dinozzo13 a écrit::ptdr: ok, est-ce que vous pourriez résumer s'il vous plaît, en reprenant précisément ce qui a été dit, la méthode de résolution dansde
avec
,
et
entiers de Gauss ainsi que toutes les conditions, parce que je suis un peu perdu avec toutes ces nouvelles informations, merci d'avance ^^.
Voilà, c'est pas très compliqué : on multiplie l'équation initiale par 1+i de chaque coté, il vient alors
Est-ce que
A vous de conclure.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
