Introduire des entiers complexes : 1°) dans les équations di
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:06
par Dinozzo13 » 16 Juil 2009, 20:06
En ce qui me concerne, c'est surtout la première partie qui me pose problème :cry: :mur: .
quand le pgcd vaut 1 je sais faire, mais lorsqu'il est différent de 1, je ne comprends pas. ne pourrait-on pas voir un autre exemple ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:08
par Dinozzo13 » 16 Juil 2009, 20:08
leon1789 a écrit:Dans un prochain exemple, on verra l'algorithme d'Euclide (étendu) dans Z[i] ...
ok ?
je veux bien, mais avant je veux comprendre la 1ere partie de la methode avec les pgcd avant de continuer, sinon je serai largué :triste: :ptdr:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:11
par leon1789 » 16 Juil 2009, 20:11
Dinozzo13 a écrit:quand le pgcd vaut 1 je sais faire, mais lorsqu'il est différent de 1,
C'est déjà ça, car on va se ramener à ce cas à un certain moment...
Dinozzo13 a écrit:je ne comprends pas. ne pourrait-on pas voir un autre exemple ?
un autre calcul de pgcd ? (on n'a pas terminer l'équation...)
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:11
par Djmaxgamer » 16 Juil 2009, 20:11
Pour reprendre :
 \times (1-i)}{(1+i) \times (1-i)} = \frac{1+3i-i+3}{2} = \frac{4+2i}{2} = 2+i)
et comme
 \in \mathbb{Z}^2)
on a :

et donc (1+3i) est divisible par 1+i
D'autre part,
 \times (1-i)}{(1+i) \times (1-i)} = \frac{-1+5i+i+5}{2} = \frac{4+6i}{2} = 2+3i)
et comme
 \in \mathbb{Z}^2)
on a :

et donc (-1+5i) est divisible par 1+i
Comme 1+i est le plus grand parmi {1,1+i} au sens de la divisibilité alors
 \wedge (-1+5i) = 1+i)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:15
par leon1789 » 16 Juil 2009, 20:15
oui, c'est exactement ça.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:15
par Djmaxgamer » 16 Juil 2009, 20:15
Regardons si 1+i divise 3+i
 \times (1-i)}{(1+i) \times (1-i)} = \frac{3-3i+i+1}{2} = \frac{4-2i}{2} = 2-i)
et comme
 \in \mathbb{Z}^2)
on a :

et donc (3+i) est divisible par 1+i
L'équation admet donc des solutions.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:17
par leon1789 » 16 Juil 2009, 20:17
exact :id:
Pour terminer, on simplifie l'équation en divisant par le pgcd (c'est possible puisqu'on vient de le vérifier !)
(1+3i)x + (1-5i)y = 3+i

(2+i)x + (2+3i)y = 2-i
Mais ici, pgcd(2+i, 2+3i)= 1 !! car on a divisé (1+3i) et (1-5i) par leur pgcd . OK ?
Donc là, on retombe dans les équations où pgcd =1 , comme hier... vous savez faire.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:18
par Dinozzo13 » 16 Juil 2009, 20:18
leon1789 a écrit:un autre calcul de pgcd ? (on n'a pas terminer l'équation...)
je sais bien mais après on sait faire, c'est la même démarche que l'équation d'hier, donc voilà.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:22
par leon1789 » 16 Juil 2009, 20:22
Dinozzo13 a écrit:je sais bien mais après on sait faire, c'est la même démarche que l'équation d'hier, donc voilà.
Ok.
On refait une recherche de pgcd via le module ?
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:24
par Djmaxgamer » 16 Juil 2009, 20:24
leon1789 a écrit:exact :id:
Pour terminer, on simplifie l'équation en divisant par le pgcd (c'est possible puisqu'on vient de la vérifier !)
(1+3i)x + (1-5i)y = 3+i

(2+i)x + (2+3i)y = 2-i
Mais ici, pgcd(2+i, 2+3i)= 1 !! car on a divisé (1+3i) et (1-5i) par leur pgcd . OK ?
Donc là, on retombe dans les équations où pgcd =1 , comme hier... vous savez faire.
une question : tu divise (ca simplifie, c'est mieux, c'est sur) mais :
parce que c'est nécessaire pour résoudre ? ou parce qu'on a déjà résolu avec pgcd=1 ? Mais c'est vrai que ne pas le faire ça serait ce compliquer la tache...
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:25
par Djmaxgamer » 16 Juil 2009, 20:25
leon1789 a écrit:Ok.
On refait une recherche de pgcd via le module ?
Maintenant que tu pose cette question, je me demande : est-ce la seule (ou meilleure en tous cas) méthode pour le trouver ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:26
par Dinozzo13 » 16 Juil 2009, 20:26
OUI, allons-y ^^.
Si vous voulez la finir, et proposer l'ensemble des solutions en guise de correction brève, je veux bien.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:27
par leon1789 » 16 Juil 2009, 20:27
Djmaxgamer a écrit:une question : tu divise (ca simplifie, c'est mieux, c'est sur) mais :
parce que c'est nécessaire pour résoudre ? ou parce qu'on a déjà résolu avec pgcd=1 ? Mais c'est vrai que ne pas le faire ça serait ce compliquer la tache...
Je vais dire (*) que le fait que pgcd = 1 est intéressant pour appliquer le théorème de Gauss (dans la partie résolution de l'équation sans second membre).
Disons que ce n'est pas nécessaire, mais pratique :zen:
(*) même si on pourrait encore détailler les choses, mais on verra plus tard...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:30
par leon1789 » 16 Juil 2009, 20:30
Dinozzo13 a écrit:OUI, allons-y ^^.
Alors pgcd(5+5i, 3+4i) ? :zen:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:32
par Dinozzo13 » 16 Juil 2009, 20:32
leon1789 a écrit:Alors pgcd(5+5i, 3+4i) ? :zen:
ouais, c'est comme si on devait résoudre (5+5i)x+(3+4i)y=c ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 20:34
par leon1789 » 16 Juil 2009, 20:34
Dinozzo13 a écrit:ouais, c'est comme si on devait résoudre (5+5i)x+(3+4i)y=c ?
oui par exemple :zen:
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:42
par Djmaxgamer » 16 Juil 2009, 20:42
Sans détailler les calculs, je trouve comme solutions :
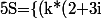-15+20i,2-16i-k*(2+i))|k\in\mathbb{Z}[i]\})
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Juil 2009, 20:48
par Dinozzo13 » 16 Juil 2009, 20:48
Djmaxgamer a écrit:Sans détailler les calculs, je trouve comme solutions :
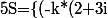-15+20i,2-16i-k*(2+i))|k\in\mathbb{Z}[i]\})
merci ^^, quand je finirai cette équation au moins j'aurais une solution pour verifier ^^
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 16 Juil 2009, 20:48
par Djmaxgamer » 16 Juil 2009, 20:48
fait gaffe j'ai corrigé yavait une erreur de signe

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Juil 2009, 21:02
par leon1789 » 16 Juil 2009, 21:02
Djmaxgamer a écrit:fait gaffe j'ai corrigé yavait une erreur de signe
c'est ok maintenant

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités

