Le voilà, correct, avec quelques annotations en couleur :
Soit d=pgcd(5+5i, 3+4i)
d divise 5+5i et 3+4i
(normal ^^)|d|^2 divise |5+5i|^2 et |3+4i|^2
(normal encore)|d|^2 divise 50 et 25
(tu calcule les modules au carré) En posant : d=a+ib avec (a,b) dans Z on a
, en remplacant :
|a+ib|^2 divise 50 et 25
a^2+b^2 divise 50 et 25
(le module au carré d'un complexe a+ib est a^2+b^2) (a^2+b^2) est dans Z
(puisque le module d'un complexe élevé au carré est dans Z (et aussi car a et b sont dans Z)) Les diviseurs communs à 50 et 25, sont, dans Z {1,5,25}
pas besoin d'expliquer ça normalement :p Le couple (a,b) peut donc être
, car a^2+b^2 peut être égal à 1, 5 ou 25 (diviseurs communs de 50 et 25) un pitit raisonnement logique donne ces possibilités pour a et b :
,( \pm 1,0),( \pm 1, \pm 2),( \pm 2, \pm 1),( \pm 3, \pm 4),( \pm 4, \pm 3)\})
d peut être alors
, comme d=a+ib :
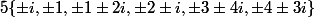
En regroupant les regroupant en égaux à un facteur inversible près :
,( \pm 1 + 2i, -2+i, -1-2i, 2-i),( \pm 1 - 2i, -2-i, -1+2i, 2+i),(3 + 4i, -4+3i,-3-4i,4-3i),(3 - 4i,-4-3i,-3+4i,4+3i)\})
De ce fait, il suffit de restreindre la recherche à
pgcd(5+5i, 3+4i) = 1 ou 1+2i ou 1-2i ou 3+4i ou 3-4i
vu que les autres pgcd possibles sont égaux à un facteur inversible près.Puisque
(1-2i)}{(1+2i)(1-2i)}=\frac{(3+4i)(1-2i)}{5}=\frac{11-2i}{5}=\frac{11}{5}-\frac{2i}{5})
Comme
 \notin \mathbb{Z}^2)
on a

et donc 1+2i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 3+4i.
De plus :
(3-4i)}{(3+4i)(3-4i)}=\frac{(5+5i)(3-5i)}{25}=\frac{35-5i}{25}=\frac{35}{25}-\frac{5i}{25} = \frac{7}{5}-\frac{i}{5})
Comme
 \notin \mathbb{Z}^2)
on a

et donc 3+4i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 5+5i.
Et encore :
(3+4i)}{(3+4i)(3-4i)}=\frac{(3+4i)(3+4i)}{25}=\frac{-7+24i}{25}=\frac{-7}{25}-\frac{24i}{25})
Comme
 \notin \mathbb{Z}^2)
on a

et donc 3-4i ne peut être pgcd de 5+5i et 3+4i car il ne divise pas 3+4i.
Et encore :
(1+2i)}{(1+2i)(1-2i)}=\frac{(3+4i)(1+2i)}{5}=\frac{-5+10i}{5}=-1+2i)
Comme
 \in \mathbb{Z}^2)
on a
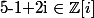
donc 1-2i divise 3+4i
De même :
(1+2i)}{(1+2i)(1-2i)}=\frac{(5+5i)(1+2i)}{5}=\frac{-5+15i}{5}=-1+3i)
Comme
 \in \mathbb{Z}^2)
on a
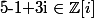
donc 1-2i divise 5+5i
1-2i est un
diviseur commun à (3+4i) et (5+5i)
De plus, 1-2i est multiple de 1, donc 1-2i est plus grand au niveau de la divisibilité que 1.
Dans ce cas :
pgcd(5+5i, 3+4i) = 1-2i
Bon là ça devrait être bon ^^
fait par
Djmaxgamer, grâce à
Leon1789dans la citation ? une erreur ?
