Initiation au symbole pi

[Dinozzo13]

Bonjour, soit une suite arithmétique ou géométrique définie pour tout . On sait que :
- lorsque est arithmétique : .
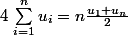
- lorsque est géométrique de raison : .
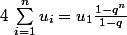
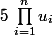
Existe-t-il donc une formule pour exprimer en fonction de : aussi bien lorsque est arithmétique ou géométrique ?

[Ericovitchi]

pour les géométriques c'est assez facile à trouver puisque les

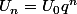
[Ben314]

Salut,

Lorsque Un est géométrique, la réponse est clairemet oui (je te laisse chercher la formule qui n'est pas dure du tout à établir)

Lorsque Un est arithmétique, la réponse n'est pas évidente, elle dépend des symboles que tu accepte d'utiliser pour écrire le résultat.
Par exemple, en supposant que U1 est un entier positif et que la raison r vaut 1, on peut écrire assez simplement le résultat en utilisant le symbole "factorielle".
Lorsque ce ne sont pas des entiers, ça ce complique pas mal.
Essaye par exemple d'écrire ce produit dans le cas de U1=1/3 et r=2/3.
Avec pas mal de bonne volonté, on arrive à écrire le résultat avec des factorielles. Y arriverais tu ?

[benekire2]

Après dans certains cas c'est même facile quand la suite v est géométrique en posant t(n)=ln(v(n)) tu exprime la somme des t ( suite arithmétique je crois) et tu en déduit le produit des v ; c'est dans quelques exos de TS si je ne m'abuse ?

PS: Pour Ben : aufait sur le topic "Initiation au symbole sigma" je serais curieux de voir une somme avec un seul indice de sommation ... ( qui doit surement exister )

[Ben314]

PS: Pour Ben : aufait sur le topic "Initiation au symbole sigma" je serais curieux de voir une somme avec un seul indice de sommation ... ( qui doit surement exister )

Petit curieux...
Tu as cherché ?

(Je te donne ra réponse sur l'autre thread...)

[benekire2]

malheureusement j'ai cherché en vain , ça me réussi pas trop les changements d'indices sur les sommations encore