Salut,je tente de résoudre ce problème: Voici ce que j'ai eu peine à trouver (a+b)(b+c)(c+a)>= 8abc
Inégalité
18 messages
- Page 1 sur 1
Inégalité
Salut,je tente de résoudre ce problème: Voici ce que j'ai eu peine à trouver (a+b)(b+c)(c+a)>= 8abc
Re: Inégalité
salut
essaie avec a=1 et b=c=-1
Indice:
tu as (a+b)²>=4ab
tu en écris deux autres et tu vois ...
essaie avec a=1 et b=c=-1
Indice:
tu as (a+b)²>=4ab
tu en écris deux autres et tu vois ...
Re: Inégalité
Je pense qu'il s'agit des dimensions d'un pavé droit.
Ton image google drive ne s'affiche pas.
Ton image google drive ne s'affiche pas.
Re: Inégalité
JérémyDubois a écrit:cela donne 0>-1
???
il y a une hypothèse à rajouter pour a, b et c
C'est vite fait avec l'indice que j'ai mis
Re: Inégalité
en fait il faut faire ouvrir l'image dans un nouvel onglet je crois.
Si vous ne voyez pas l'énoncé le voici:
(a+b)(b+c)(c+a) >= 8(a+b-c)(b+c-a) (c+a-b)
Voici ce j'ai trové pour l'instant, (a+b)(b+c)(c+a) >= 8abc
Si vous ne voyez pas l'énoncé le voici:
(a+b)(b+c)(c+a) >= 8(a+b-c)(b+c-a) (c+a-b)
Voici ce j'ai trové pour l'instant, (a+b)(b+c)(c+a) >= 8abc
Re: Inégalité
salut
peux-tu nous donner un énoncé exact et complet ?
peux-tu nous donner un énoncé exact et complet ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Inégalité
(a+b)(b+c)(c+a) >= 8(a+b-c)(b+c-a) (c+a-b) et a,b,c points d'un triangle
j'ai trouvé que (a+b)(b+c)(c+a) >= 8abc ensuite je bloque
j'ai trouvé que (a+b)(b+c)(c+a) >= 8abc ensuite je bloque
Re: Inégalité
donc tu additionnes des points et multiplies dessomme de points ...JérémyDubois a écrit:(a+b)(b+c)(c+a) >= 8(a+b-c)(b+c-a) (c+a-b) et a,b,c points d'un triangle
j'ai trouvé que (a+b)(b+c)(c+a) >= 8abc ensuite je bloque
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Inégalité
j'ai trouvé que (a+b)(b+c)(c+a) >= 8abc
pose :
x=a+b-c
y=b+c-a
z=c+a-b
utilise ce que tu as démontré:
(x+y)(y+z)(z+x) >= ...
Re: Inégalité
Bonjour ;
Je détaille la méthode de chan79 :
1) \in \mathbb R^+} \times \mathbb R^+ : (\sqrt x - \sqrt y)^2 = x + y - 2 \sqrt{xy} \ge 0 \Rightarrow 2 \sqrt{xy} \le x + y ,)
donc \in \mathbb R^{+3} : 2 \sqrt{xy} \le x + y ; 2 \sqrt{yz} \le y+z ; 2 \sqrt{zx} \le z+x)
donc(y+z)(z+x).)
Soient a , b et c les longueurs des côtés d'un triangle , donc en appliquant l'inégalité triangulaire , on a :
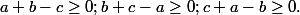
Je finis comme chan79 en posant dans l'négalité déjà trouvée :
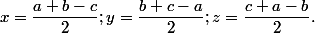
P.S : je me demande où est-ce qu'il est passé JérémyDubois ?
Je détaille la méthode de chan79 :
1)
donc
donc
Soient a , b et c les longueurs des côtés d'un triangle , donc en appliquant l'inégalité triangulaire , on a :
Je finis comme chan79 en posant dans l'négalité déjà trouvée :
P.S : je me demande où est-ce qu'il est passé JérémyDubois ?
Re: Inégalité
Excuses-moi zygomatique je voulais dire les côtés.
Je comprends aymanemaysae mais pourquoi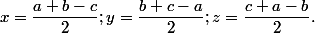
Je comprends aymanemaysae mais pourquoi
Re: Inégalité
j'étais parti de l'idée suivante où on pose s = a + b + c :
(b + c)(c + a) = (s - a)(s - b)(s - c) = s^3 - (a + b + c)s^2 + (ab + bc + ca)s - abc = (ab + bc + ca)s - abc)
mais je n'arrivais pas à conclure ... donc j'ai laissé tombé ...
et j'ai trouvé une démonstration où l'auteur conclut directement pars - abc \ge 8abc) ... mais je ne comprends pas pourquoi ...
... mais je ne comprends pas pourquoi ...
si une âme charitable pouvait m'éclairer ....
mais je n'arrivais pas à conclure ... donc j'ai laissé tombé ...
et j'ai trouvé une démonstration où l'auteur conclut directement par
si une âme charitable pouvait m'éclairer ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Inégalité
zygomatique a écrit:j'étais parti de l'idée suivante où on pose s = a + b + c :
mais je n'arrivais pas à conclure ... donc j'ai laissé tombé ...
et j'ai trouvé une démonstration où l'auteur conclut directement par... mais je ne comprends pas pourquoi ...
si une âme charitable pouvait m'éclairer ....
Hi Zygo,
Applique AM-GM (inégalité arithmético-géométrique) à:
(a+b+c)/3 > (abc)^(1/3)
(ab+bc + ac)/3 > (abc)^(2/3)
Par produit membre à membre:
(a+b+c)(ab+bc+ac) > 9 abc
(ab+bc+ac)*S - abc > 8abc
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Inégalité
merci ... mais l'auteur le propose comme autre méthode : https://www-fourier.ujf-grenoble.fr/~ro ... eChap2.pdf (bas de la deuxième page et suivante)
et je ne vois toujours pas comment conclure directement ...
et je ne vois toujours pas comment conclure directement ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Inégalité
Dans la question 3
il développe (b+c)(a+b)(a+c)
en remplaçant en fonction de S, puisque S=a+b+c, on a S-a=b+c... idem pour les autres
il développe et réduit le polynôme de variable S
Ensuite il remplace a+b+c par S et obtient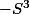 qui s'élimine avec
qui s'élimine avec 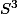
Il utilise enfin que le produit calculé est supérieur à 8abc d'après le 2° ce qui permet de conclure
il développe (b+c)(a+b)(a+c)
en remplaçant en fonction de S, puisque S=a+b+c, on a S-a=b+c... idem pour les autres
il développe et réduit le polynôme de variable S
Ensuite il remplace a+b+c par S et obtient
Il utilise enfin que le produit calculé est supérieur à 8abc d'après le 2° ce qui permet de conclure
Re: Inégalité
hhhhhhaaaaaaaaaaaaaaaaaaaaa mais oui ok ... mais quel con suis-je !!!
PS : j'avais bien compris toute le développement (que j'avais trouvé moi-même) mais c'était cette minoration qui m'em...
merci !!
PS : j'avais bien compris toute le développement (que j'avais trouvé moi-même) mais c'était cette minoration qui m'em...
merci !!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
