Bonsoir à tous,
J'aimerai savoir pourquoi une fonction n'est pas dérivable lorsque la tangente est verticale? Je n'arrive pas à comprendre...
Merci d'avance :++:
Fonction dérivée
11 messages
- Page 1 sur 1
Et graphiquement parlant? Enfin par exemple j'ai devant mes yeux un graphique avec une fonction et une tangente verticale au point A. Il est demandé de calculer le nombre dérivé (donc avec le coefficient directeur) mais comme la tangente est vertical il n'y en a pas. Mais comment l'expliquer simplement?
salut
une courbe peut effectivement avoir une tangente en un point sans que la fonction associée soit effectivement dérivable en l'abscisse de ce point : c'est le cas de la fonction racine carrée en 0
tout simplement parce que la définition du nombre dérivé ... c'est que c'est un nombre !!!
:ptdr:
plus précisément la limite du taux de variation existe donc est un nombre fini ...
et si tu nous donnais la fonction dont tu parles ?
une courbe peut effectivement avoir une tangente en un point sans que la fonction associée soit effectivement dérivable en l'abscisse de ce point : c'est le cas de la fonction racine carrée en 0
tout simplement parce que la définition du nombre dérivé ... c'est que c'est un nombre !!!
:ptdr:
plus précisément la limite du taux de variation existe donc est un nombre fini ...
et si tu nous donnais la fonction dont tu parles ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
une courbe peut effectivement avoir une tangente en un point sans que la fonction associée soit effectivement dérivable en l'abscisse de ce point : c'est le cas de la fonction racine carrée en 0
tout simplement parce que la définition du nombre dérivé ... c'est que c'est un nombre !!!
:ptdr:
plus précisément la limite du taux de variation existe donc est un nombre fini ...
et si tu nous donnais la fonction dont tu parles ?
Mais je ne comprends pas pourquoi la limite d'une tangente verticale n'est pas fini?
Elsapseudo a écrit:Et graphiquement parlant? Enfin par exemple j'ai devant mes yeux un graphique avec une fonction et une tangente verticale au point A. Il est demandé de calculer le nombre dérivé (donc avec le coefficient directeur) mais comme la tangente est vertical il n'y en a pas. Mais comment l'expliquer simplement?
Bonsoir,
La pente de la tangente de f en
Question : Quelle est l'"allure" (horizontal, vertical, oblique) de la droite d'équation
Salut !
Un petit raisonnement qui éclairera probablement ta lanterne :
Rappel : Une équation de la tangente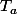 à la courbe représentative
à la courbe représentative  d'une fonction
d'une fonction  au point d'abscisse
au point d'abscisse  est donnée par :
est donnée par : 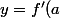 (x-a) +f(a)) (sous réserve que
(sous réserve que  soit dérivable en
soit dérivable en  , sinon f'(a) n'est pas défini).
, sinon f'(a) n'est pas défini).
Une droite verticale admet pour équation , donc
, donc 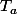 est verticale si et seulement si on peut l'écrire sous la forme
est verticale si et seulement si on peut l'écrire sous la forme  . Pour cela, on a :
. Pour cela, on a :
[CENTER]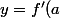 (x-a) +f(a)) équivaut à
équivaut à } y- \frac{f(a)}{ f'(a)} + a)
[/CENTER]
( \ne 0) car sinon
car sinon 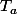 serait horizontale).
serait horizontale).
Ensuite, le seul moyen pour "neutraliser " et rendre ainsi le membre de droite consnant, est de faire tendre
" et rendre ainsi le membre de droite consnant, est de faire tendre ) vers
vers  ou
ou  (cela aura pour effet de faire tendre
(cela aura pour effet de faire tendre } y) vers
vers  ).
).
:+++:
Un petit raisonnement qui éclairera probablement ta lanterne :
Rappel : Une équation de la tangente
Une droite verticale admet pour équation
[CENTER]
[/CENTER]
(
Ensuite, le seul moyen pour "neutraliser
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:alors tu ne sais pas ce qu'est un nombre dérivé ....
Bon, pour faire simple et relier ceci au graphique:
le nombre dérivé f'(a) (s'il existe) est le coefficient directeur de la tangente en un point A d'abscisse a
et une droite parallèle à l'axe des ordonnées n'a pas de coeff directeur.
Rappel: équation réduite d'une droite non parallèle à l'axe des ordonnées y=mx+p
et si la droite est parallèle à l'axe des ordonnées, elle admet une équation de la forme x=constante
J F L
Elsapseudo a écrit:Mais je ne comprends pas pourquoi la limite d'une tangente verticale n'est pas fini?
La limite d'une tangente, cela ne veut rien dire. Une tangente, c'est une limite en soi. Tu veux parler de la limite du taux d'accroissement, ou bien de la limite de la sécante ?
Derrière ta question, il y a : pourquoi on ne considère pas qu'une fonction est dérivable quand la tangente à la courbe a une position verticale ?
Parce que l'infini n'est pas un "nombre" et on ne pourrait plus parler de fonction dérivée sur un intervalle où la courbe contient une tangente verticale, et parce que si on considère que la fonction est dérivable sur un tel intervalle, il y a tout un tas de théorèmes qui utilisent les dérivées qui ne s'appliqueraient plus, notamment le théorème des accroissements finis...
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

