Développement décimal d'un irrationnel
34 messages
- Page 1 sur 2 - 1, 2
Développement décimal d'un irrationnel
Bonjour,
Je me suis posé une question sous la forme d'un exercice, mais je sais même pas si c'est démontrable, aidez-moi svp je ne trouve rien sur internet.
Soit x un irrationnel quelconque:
{x} = a1.10^(-1) + a2.10^(-2) + ... + an.10^(-n)
On a pour tout n, an appartient à { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
On peut définir la série qui à chaque nombre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 associe le nombre de fois qu'il apparaît dans le développement décimal de x.
La question c'est de savoir quand n tend vers + inf si l'écart type de cette série tend vers 0.
Merci!
Je me suis posé une question sous la forme d'un exercice, mais je sais même pas si c'est démontrable, aidez-moi svp je ne trouve rien sur internet.
Soit x un irrationnel quelconque:
{x} = a1.10^(-1) + a2.10^(-2) + ... + an.10^(-n)
On a pour tout n, an appartient à { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
On peut définir la série qui à chaque nombre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 associe le nombre de fois qu'il apparaît dans le développement décimal de x.
La question c'est de savoir quand n tend vers + inf si l'écart type de cette série tend vers 0.
Merci!
La modestie s'apprend par la répétition de l'échec.
Salut,
Je trouve ta question intéressante !
Mais j'avoue ne pas bien comprendre comment calculer l'écart-type d'une série statistique.. infinie?
Pour un rationnel déjà comment? Par exemple 1/9 = 0,111....
Je veux bien "admettre" que l'écart-type vaut 0. Mais par exemple pour
1/7 comment tu fais?
Je trouve ta question intéressante !
Mais j'avoue ne pas bien comprendre comment calculer l'écart-type d'une série statistique.. infinie?
Pour un rationnel déjà comment? Par exemple 1/9 = 0,111....
Je veux bien "admettre" que l'écart-type vaut 0. Mais par exemple pour
1/7 comment tu fais?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Lostounet a écrit:Salut,
Je trouve ta question intéressante !
Mais j'avoue ne pas bien comprendre comment calculer l'écart-type d'une série statistique.. infinie?
Pour un rationnel déjà comment? Par exemple 1/9 = 0,111....
Je veux bien "admettre" que l'écart-type vaut 0. Mais par exemple pour
1/7 comment tu fais?
Déjà merci pour cette réponse!
Je crois que tout rationnel a une partie de son développement décimal qui se répète à un certain moment. Par exemple 1/7 c'est 0.14285714285 ( pour les 11 premières décimales ) donc le motif se répétant c'est 142857. Donc il va y avoir autant de 1 que de 2 que 4 de 5 de 7 ou de 8. Dans ce cas là, on pourrais considérer seulement la série définie avec les chiffres du motif se répétant. Et l'écart type c'est bien 0 dans ce cas-là. Mais sinon en considérant l'écart type sur tous les chiffres on peut dire qu'il est croissant avec n. En effet les écarts à la moyenne entre les chiffres qui ne sont pas dans le motif se répétant va augmenter proportiennellement à la moyenne ( qui augmente avec n ) tandis que les autres écarts seront nuls ou presque.
( Je dis peut être n'importe quoi, corrigez-moi )
Mais pour les irrationnels ça me semble plus dur ( et effectivement intéréssant ).
La modestie s'apprend par la répétition de l'échec.
Pourquoi l'écart-type du motif de 1/7 vaut-il 0 ?
1 4 2 8 5 7 a un écart-type de 2,7 environ.
Mais si tu ajoutes le "1" du motif suivant, l'écart-type va passer à 2.8
Si tu ajoutes le "4" qui suit, l'écart-type passe à 2,6
Donc je pense que l'écart-type va "changer" au fur et à mesure que tu ajoutes des bouts du motif suivant... C'est combien l'écart-type au final alors sachant que le développement de 1/7 est infini ?
Modif: Je relis ton post modifié
1 4 2 8 5 7 a un écart-type de 2,7 environ.
Mais si tu ajoutes le "1" du motif suivant, l'écart-type va passer à 2.8
Si tu ajoutes le "4" qui suit, l'écart-type passe à 2,6
Donc je pense que l'écart-type va "changer" au fur et à mesure que tu ajoutes des bouts du motif suivant... C'est combien l'écart-type au final alors sachant que le développement de 1/7 est infini ?
Modif: Je relis ton post modifié
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Lostounet a écrit:Pourquoi l'écart-type du motif de 1/7 vaut-il 0 ?
1 4 2 8 5 7 a un écart-type de 2,7 environ.
Mais si tu ajoutes le "1" du motif suivant, l'écart-type va passer à 2.8
Si tu ajoutes le "4" qui suit, l'écart-type passe à 2,6
Donc je pense que l'écart-type va "changer" au fur et à mesure que tu ajoutes des bouts du motif suivant... C'est combien l'écart-type au final alors sachant que le développement de 1/7 est infini ?
Modif: Je relis ton post modifié
Je comprends ce que vous dites mais dans la série que je définis, les nombres ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ) sont associés au nombre de fois où il apparaissent dans le développement décimal.
La modestie s'apprend par la répétition de l'échec.
Ah ok, donc tu considères qu'il y a "autant" de 1, 4, 2, 8, 5 et 7 dans le développement de 1/7...
Est-ce que dans le développement de racine de 2 il y a un chiffre qui apparait plus souvent que les autres... je ne sais pas !
Est-ce que dans racine de (2) on pourrait trouver par exemple le motif 142857 autant de fois que l'on veut ? Et le motif 0000000 ?
:id:
Est-ce que dans le développement de racine de 2 il y a un chiffre qui apparait plus souvent que les autres... je ne sais pas !
Est-ce que dans racine de (2) on pourrait trouver par exemple le motif 142857 autant de fois que l'on veut ? Et le motif 0000000 ?
:id:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Salut,
Oui, y a t-il une erreur?
Je ne sais pas en fait ( pour pi c'est une propriété vérifiée, je crois que ce sont les nombres " univers " ). Ce problème m'a été inspiré sur les recherches statistiques sur les décimales de pi. On voyait que pour par exemple 10^6 décimale, il y avait environ le même nombre de 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ( environ 100000 ). Et donc (expérimentalement ) l'écart type tend vers 0 quand n tend vers + inf.
C'est pourquoi j'emettais l'hypothèse que tout nombre irrationnel avait ce comportement.
Lostounet a écrit:
Ah ok, donc tu considères qu'il y a "autant" de 1, 4, 2, 8, 5 et 7 dans le développement de 1/7...
Oui, y a t-il une erreur?
Lostounet a écrit:
Est-ce que dans le développement de racine de 2 il y a un chiffre qui apparait plus souvent que les autres... je ne sais pas !
Est-ce que dans racine de (2) on pourrait trouver par exemple le motif 142857 autant de fois que l'on veut ? Et le motif 0000000 ?
:id:
Je ne sais pas en fait ( pour pi c'est une propriété vérifiée, je crois que ce sont les nombres " univers " ). Ce problème m'a été inspiré sur les recherches statistiques sur les décimales de pi. On voyait que pour par exemple 10^6 décimale, il y avait environ le même nombre de 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ( environ 100000 ). Et donc (expérimentalement ) l'écart type tend vers 0 quand n tend vers + inf.
C'est pourquoi j'emettais l'hypothèse que tout nombre irrationnel avait ce comportement.
La modestie s'apprend par la répétition de l'échec.
alexis6 a écrit:Salut,
Oui, y a t-il une erreur?
Je ne sais pas en fait ( pour pi c'est une propriété vérifiée, je crois que ce sont les nombres " univers " ). Ce problème m'a été inspiré sur les recherches statistiques sur les décimales de pi. On voyait que pour par exemple 10^6 décimale, il y avait environ le même nombre de 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ( environ 100000 ). Et donc (expérimentalement ) l'écart type tend vers 0 quand n tend vers + inf.
C'est pourquoi j'emettais l'hypothèse que tout nombre irrationnel avait ce comportement.
Le fait que pi et racine de 2 soient des nombres univers n'a jamais été démontré.
chombier a écrit:Le fait que pi et racine de 2 soient des nombres univers n'a jamais été démontré.
Ah bon. J'ai du me trompé alors. De toute façon je pense quse ma question ne marche pas pour tous les irrationnels. Par exemple si j'associe à un nombre de N 0 si il composé et 1 si il est premier, je vais avoir une suite de 0 et de 1 du genre 011010100010100...
Ensuite si je transforme ce nombre en 0,011010100010100 0... il est clairement irrationnel. Pourtant le nombre de nombre premier ( donc de 1 ) se raréfie donc il y aura plus de 0 que de 1.
En fait ma question était posée bizzarement mais c'était: dans tout développement décimal d'un irrationnel, y a t-il au bout d'un moment autant de 1 que de 2 que de 3...
La modestie s'apprend par la répétition de l'échec.
mathafou a écrit:tu viens de donner toi-même un contre exemple :zen:
Oui j'avais remarqué... D'où : " De toute façon je pense que ma question ne marche pas pour tous les irrationnels ". Donc en effet ça ne marche pas tout le temps ( mais alors quand est ce que ça marche? )
La modestie s'apprend par la répétition de l'échec.
salut
un irrationnel étant infini l'effectif de chaque chiffre est infini ...
si à un irrationnel x on associe les trois suites ::
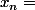 troncature de x à
troncature de x à 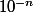
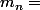 moyenne des chiffres de
moyenne des chiffres de 
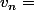 variance des chiffres de
variance des chiffres de  (carré de l'écart type)
(carré de l'écart type)
alors tout ce qu'on peut dire :
la suite) converge vers x (trivialité)
converge vers x (trivialité)
les suites \ et \ (v_n)) sont bornées
sont bornées
si on suppose qu'il y a équirépartition des chiffres alors ::
 = 4,5)
 - \dfrac {81}4 = \dfrac {33}4)
soit un écat type d'environ 2,87 ...
:lol3:
je ne comprends pas cette phrase ::
un irrationnel étant infini l'effectif de chaque chiffre est infini ...
si à un irrationnel x on associe les trois suites ::
alors tout ce qu'on peut dire :
la suite
les suites
si on suppose qu'il y a équirépartition des chiffres alors ::
soit un écat type d'environ 2,87 ...
:lol3:
je ne comprends pas cette phrase ::
Par exemple si j'associe à un nombre de N 0 si il composé et 1 si il est premier, je vais avoir une suite de 0 et de 1 du genre 011010100010100...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
alexis6 a écrit:Oui j'avais remarqué... D'où : " De toute façon je pense que ma question ne marche pas pour tous les irrationnels ". Donc en effet ça ne marche pas tout le temps ( mais alors quand est ce que ça marche? )
c'est fortement lié à la définition d'un nombre normal
tu touches là à des questions difficiles... qui possèdent relativement peu de résultats concrets
et le caractère non dénombrable de ces ensembles rend encore plus difficile l'interprétation de "la plupart des nombre sont normaux"
en comparaison avec le complément qui affirme qu'il existe une infinité non dénombrable de nombres pas normaux (les pauvres)
PS : en plus la confusion sur la notion d'écart type n'aide pas à clarifier ta vraie question par rapport à ce que tu en écris ...
En reprenant le raisonnement de zygomatique
si à un irrationnel x on associe les trois suites :
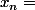 troncature de x à
troncature de x à 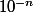
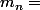 moyenne des effectifs des chiffres de
moyenne des effectifs des chiffres de 
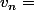 variance des effectifs des chiffres de
variance des effectifs des chiffres de  (carré de l'écart type)
(carré de l'écart type)
si on suppose qu'il y a équirépartition des chiffres alors leur effectif tendent vers le même nombre a:
 = a)
^2 + (a-a)^2 + (a-a)^2 + ... + (a-a)^2 + (a-a)^2) = 0)
soit un écart type d'environ 0 ...
:lol3:
Je vais me renseigner pour les nombres normaux de mathafou sinon. Je viens de voir le lien rapidement et effectivement pour l'instant il n'y a que des conjectures, c'est un domaine à explorer... Je suis content de m'être posé par moi même une question qui n'a pas encore de réponse.
si à un irrationnel x on associe les trois suites :
si on suppose qu'il y a équirépartition des chiffres alors leur effectif tendent vers le même nombre a:
soit un écart type d'environ 0 ...
:lol3:
Je vais me renseigner pour les nombres normaux de mathafou sinon. Je viens de voir le lien rapidement et effectivement pour l'instant il n'y a que des conjectures, c'est un domaine à explorer... Je suis content de m'être posé par moi même une question qui n'a pas encore de réponse.
La modestie s'apprend par la répétition de l'échec.
zygomatique a écrit:c'est évidemment faux ...
un écart type nul équivaut à ce que la série (statistique) ne prend qu'une seule valeur ....
et revois le calcul d'une moyenne ....
Oui sauf que là il s'agit de limites non? On calcule bien l'écart type quand n-->+inf?
La série ne prend effectivement qu'une seule valeur en +inf si on suppose que les effectifs tendent tous vers a.
La modestie s'apprend par la répétition de l'échec.
n'importe quoi .....
on considère le décimal troncature à l'ordre n .... pour n très très très très .... très grand .....
troncature à l'ordre n .... pour n très très très très .... très grand .....
sa partie décimale est donc constituée des 10 chiffres 0, 1, ...., 9....
si on suppose que ça tend vers une équirépartition alors il y a n/10 0, n/10, 1, n/10 2, ... et n/10 9
donc = 4,5)
....
on considère le décimal
sa partie décimale est donc constituée des 10 chiffres 0, 1, ...., 9....
si on suppose que ça tend vers une équirépartition alors il y a n/10 0, n/10, 1, n/10 2, ... et n/10 9
donc
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Salut,
J'ai pas trop compris non plus ce que tu appelais "l'écart type" du bidule (surtout du fait que je vois franchement pas ce que tu a pu calculer pour trouver que ça tend vers 0).
Sinon, quasi par construction (des réels), la suite des décimales d'un réel peut être absolument quelconque, modulo la petite exception que les nombres décimaux ont deux écritures décimales : une dite "propre" avec que des 0 à partir d'un certain rang et l'autre avec que des 9 à partir d'un certain rang.
Donc, vu que les décimales d'un réel peuvent être absolument tout ce que tu veut, tu n'aura aucune propriété "remarquable" concernant les chiffres qui apparaissent dans l'écriture de tout les réels.
Après, évidement, tu peut te restreindre à une classe particulière de réels (par exemple les rationnels) dans laquelle il y a éventuellement des choses à dire.
J'ai pas trop compris non plus ce que tu appelais "l'écart type" du bidule (surtout du fait que je vois franchement pas ce que tu a pu calculer pour trouver que ça tend vers 0).
Sinon, quasi par construction (des réels), la suite des décimales d'un réel peut être absolument quelconque, modulo la petite exception que les nombres décimaux ont deux écritures décimales : une dite "propre" avec que des 0 à partir d'un certain rang et l'autre avec que des 9 à partir d'un certain rang.
Donc, vu que les décimales d'un réel peuvent être absolument tout ce que tu veut, tu n'aura aucune propriété "remarquable" concernant les chiffres qui apparaissent dans l'écriture de tout les réels.
Après, évidement, tu peut te restreindre à une classe particulière de réels (par exemple les rationnels) dans laquelle il y a éventuellement des choses à dire.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
zygomatique a écrit:n'importe quoi .....
on considère le décimaltroncature à l'ordre n .... pour n très très très très .... très grand .....
sa partie décimale est donc constituée des 10 chiffres 0, 1, ...., 9....
si on suppose que ça tend vers une équirépartition alors il y a n/10 0, n/10, 1, n/10 2, ... et n/10 9
donc
....
Pas la peine de me prendre de haut hein. Je prétends pas avoir la vérité justement je pose des questions.
La modestie s'apprend par la répétition de l'échec.
alexis6 a écrit:Pas la peine de me prendre de haut hein. Je prétends pas avoir la vérité justement je pose des questions.
je ne te prends pas de haut ....
c'est très bien de te questionner et d'être curieux ....
mais là tu as dit de très grosses bêtises sur de choses très élémentaires ...(calcul d'une moyenne) ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
