Les dattes à Dattier
Les dattes à Dattier
Salut,
Je vais proposer des énigmes originales de maths qui ont une réponse de moins d'une dizaine de lignes niveaux max agreg.
Cordialement.
Je vais proposer des énigmes originales de maths qui ont une réponse de moins d'une dizaine de lignes niveaux max agreg.
Cordialement.
Modifié en dernier par Dattier le 06 Juin 2019, 10:55, modifié 1 fois.
Re: Les dattes à Dattier
1 : une question de bijectivité résolue par GaBuZoMeu
Soit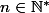 , et
, et 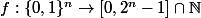 tel que, pour
tel que, pour $, avec $a_i \in \mathbb N) .
.
Trouver une CNS sur les pour que
pour que  soit bijective.
soit bijective.
2 : caractérisation séquentielle des sigma-compacts résolue par Perroquet
Soit) un espace munit d'une topologie, on dit que
un espace munit d'une topologie, on dit que  est sigma-compact si :
est sigma-compact si :
pour tout recouvrement infini d'ouvert_{i\in I}) il en existe un sous-recouvrement dénombrable
il en existe un sous-recouvrement dénombrable _{n \in \mathbb N}) .
.
Dans le cas d'un espace métrique, déterminer une caractérisation séquentielle de la sigma-compacité.
3 : Borne sur les sigma-compacts résoule par Perroquet
a/ Existe-t-il une borne du cardinal atteinte sur les compacts métriques ?
b/ Existe-t-il une borne du cardinal atteinte sur les sigma-compacts métriques ?
4 : calcul exact avec la partie entière résolue par Perroquet
Soit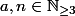 tel que
tel que =1$) . A-t-on
. A-t-on =\dfrac{a\times n+a-n+1}{2} $$) ?
?
5 : suite récurrente non linéaire : résolue par Perroquet
^2}$) et
et 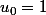 . Calculer
. Calculer  \mod (3^{90}-2)$) .
.
Avec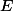 la partie entière :
la partie entière : =23)
Soit
Trouver une CNS sur les
2 : caractérisation séquentielle des sigma-compacts résolue par Perroquet
Soit
pour tout recouvrement infini d'ouvert
Dans le cas d'un espace métrique, déterminer une caractérisation séquentielle de la sigma-compacité.
3 : Borne sur les sigma-compacts résoule par Perroquet
a/ Existe-t-il une borne du cardinal atteinte sur les compacts métriques ?
b/ Existe-t-il une borne du cardinal atteinte sur les sigma-compacts métriques ?
4 : calcul exact avec la partie entière résolue par Perroquet
Soit
5 : suite récurrente non linéaire : résolue par Perroquet
Avec
Modifié en dernier par Dattier le 22 Juin 2019, 08:31, modifié 3 fois.
Re: Les dattes à Dattier
6 : inégalité de Jensen+
Soient$) et
et )$.)
A-t-on)\text{d}x-g\left(\int_0^1 f(x) \text{d}x\right)\right| \leq 2 \max(|g''|)\times \max(|f|) \times \max(|f'|)) ?
?
7 : fontion sous-lipschitzienne
Soit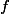 une fonction de
une fonction de ) métrique dans
métrique dans ) .
.
On dit que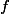 est sous-lipschitzienne ssi
est sous-lipschitzienne ssi 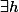 réel continue croissante tel que
réel continue croissante tel que ,f(y)) \leq h(d_E(x,y))$) et
et =0$) .
.
Soit$) fonction quelconque, avec
fonction quelconque, avec 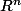 munit d'une norme
munit d'une norme 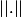
A-t-on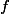 continue ssi
continue ssi 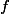 est sous-lipschitzienne ?
est sous-lipschitzienne ?
8 : Cosinus et liberté résolue par Oty
Existe-t-il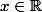 tel que
tel que \}_{n \in \mathbb N}$) soit
soit 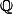 -libre ?
-libre ?
9 : Fonction polyssante :
Une fonction polyssante est une fonction de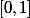 dans les réels, tel qu'il existe un polynôme
dans les réels, tel qu'il existe un polynôme 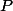 non constant à 4 variables tel que :
non constant à 4 variables tel que : ,x,f(y),y) \geq 0$) .
.
a/ Y-a-t-il des fonctions polyssantes tel quelles soient croissante, 1-lipschtiz ou 1/2-holderienne ?
b/ Existe-t-il P polynôme tel que toutes les fonctions continues de [0,1] dans les réels soit P-polyssante avec les fonctions discontinues non-P-polyssante ?
10 : Série alternée en cascade résolue par Hichamalpha
Soit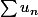 une série alternée, est-ce que la série de terme générale
une série alternée, est-ce que la série de terme générale  est aussi alternée ?
est aussi alternée ?
Soient
A-t-on
7 : fontion sous-lipschitzienne
Soit
On dit que
Soit
A-t-on
8 : Cosinus et liberté résolue par Oty
Existe-t-il
9 : Fonction polyssante :
Une fonction polyssante est une fonction de
a/ Y-a-t-il des fonctions polyssantes tel quelles soient croissante, 1-lipschtiz ou 1/2-holderienne ?
b/ Existe-t-il P polynôme tel que toutes les fonctions continues de [0,1] dans les réels soit P-polyssante avec les fonctions discontinues non-P-polyssante ?
10 : Série alternée en cascade résolue par Hichamalpha
Soit
Modifié en dernier par Dattier le 11 Juin 2019, 18:58, modifié 1 fois.
Re: Les dattes à Dattier
11 : CNS de bijectivité
Soit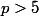 un nombre permier,
un nombre permier, 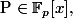 tel que
tel que =3$) .
.
Trouver une CNS sur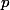 et les coeffs de
et les coeffs de 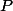 pour que
pour que 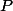 soit une bijection de
soit une bijection de 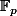 dans lui même.
dans lui même.
12 : Casser Diffie-Hellman
Montrer que casser Diffie-Hellman, revient à pouvoir calculer=b^{i^2}) avec
avec  élement générateur du groupe multiplicatif, sur
élement générateur du groupe multiplicatif, sur 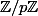 avec
avec  premier.
premier.
13 : l'improbable résultat 2
Soit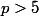 un nombre premier,
un nombre premier, 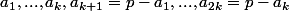 une sequence finie d'entier distincts de
une sequence finie d'entier distincts de 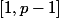 , avec
, avec 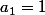
tel que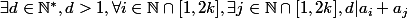
et<d) .
.
A-t-on :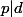 ?
?
14 : Polynôme et diviseur résolue par FLBP et Perroquet
>1. \text{ A-t-on } \forall n\in\mathbb N^*, n!| P(1)\times P(2) ...\times P(n), \text{ ssi } \exists a\in \mathbb Z, P(a)=0 ?)
15 : Recouvrement minimal
Soit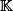 un corps fini,
un corps fini, 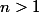 un entier, on se place dans le
un entier, on se place dans le 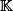 -ev
-ev 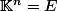 .
.
Combien au minimum faut-il d'hyper-plans pour recouvrir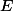 ?
?
Soit
Trouver une CNS sur
12 : Casser Diffie-Hellman
Montrer que casser Diffie-Hellman, revient à pouvoir calculer
13 : l'improbable résultat 2
Soit
tel que
et
A-t-on :
14 : Polynôme et diviseur résolue par FLBP et Perroquet
15 : Recouvrement minimal
Soit
Combien au minimum faut-il d'hyper-plans pour recouvrir
Modifié en dernier par Dattier le 13 Juin 2019, 08:30, modifié 5 fois.
Re: Les dattes à Dattier
15 : hyperplans affines : 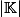 , hyperplans vectoriels :
, hyperplans vectoriels : 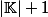 .
.
Je me souviens que tu l'avais déjà posé, et que le résultat t'avait étonné (tu pensais que c'était plus).
Je me souviens que tu l'avais déjà posé, et que le résultat t'avait étonné (tu pensais que c'était plus).
Re: Les dattes à Dattier
Oui, exacte.
PS : il y a aussi le 8 qui a été résolu (sur un autre forum).
PS : il y a aussi le 8 qui a été résolu (sur un autre forum).
Re: Les dattes à Dattier
16 : L'ensemble de Brouwer
$) est l'ensemble des fonctions continues avec un point fixe, munit de la norme uniforme.
est l'ensemble des fonctions continues avec un point fixe, munit de la norme uniforme.
a/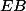 est-il fermé ?
est-il fermé ?
b/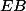 est-il d'intérieur non vide ?
est-il d'intérieur non vide ?
c/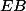 est-il connexe ?
est-il connexe ?
17 : Toute fonction est-elle continue ? résolue par GaBuZoMeu
Soit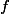 une fonction réel quelconque. Existe-t-il,
une fonction réel quelconque. Existe-t-il, 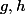 des bijections réels tel que :
des bijections réels tel que : 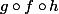 soit continue ?
soit continue ?
18 : la vraie bijection résolue par Perroquet
Si A est en vrai bijection avec B sous parties de et A
et A 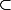 B alors A=B : (1)
B alors A=B : (1)
Si A et B finies sous parties de , alors A et B sont en vrai bijection ssi card(A)=card(B) : (2)
, alors A et B sont en vrai bijection ssi card(A)=card(B) : (2)
Trouvez une définition de la vraie bijection des sous parties de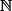 , tel que :
, tel que :
(1) et (2) soient vraies.
19 : Compact radin résolue par Perroquet
Un compact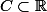 est dit radin, s'il existe
est dit radin, s'il existe _n) tel que
tel que 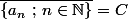 et
et
 , avec
, avec >\text{card}(\mathbb N).)
Existe-t-il un compact radin ?
20 : commutativité et point fixe
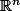 euclidien avec
euclidien avec 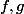 2 fonctions continues de la boule unité, vers la boule unité, avec
2 fonctions continues de la boule unité, vers la boule unité, avec 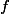 1-lipschitz et
1-lipschitz et 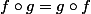 .
.
A-t-on l'existence d'un point fixe commun à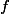 et
et 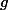 ?
?
a/
b/
c/
17 : Toute fonction est-elle continue ? résolue par GaBuZoMeu
Soit
18 : la vraie bijection résolue par Perroquet
Si A est en vrai bijection avec B sous parties de
Si A et B finies sous parties de
Trouvez une définition de la vraie bijection des sous parties de
(1) et (2) soient vraies.
19 : Compact radin résolue par Perroquet
Un compact
Existe-t-il un compact radin ?
20 : commutativité et point fixe
A-t-on l'existence d'un point fixe commun à
Modifié en dernier par Dattier le 15 Juin 2019, 22:22, modifié 5 fois.
Re: Les dattes à Dattier
Modifié en dernier par Dattier le 11 Juin 2019, 19:00, modifié 1 fois.
Re: Les dattes à Dattier
Modifié en dernier par Dattier le 11 Juin 2019, 19:02, modifié 1 fois.
Re: Les dattes à Dattier
23 : Super théorème de l'application ouverte
Soit fonction linéaire bijective de
fonction linéaire bijective de ,||.||_\infty)) dans lui même. A-t-on
dans lui même. A-t-on  continue ?
continue ?
Soit
Re: Les dattes à Dattier
Ben , un à la fois ça peut être amusant ( pour certains) mais le paquet en entier c'est vraiment trop lourd 
Imod

Imod
Re: Les dattes à Dattier
Tu n'en choisies qu'un à la fois, aprés cela ferait trop de fil, je prèfére tout regrouper dans un seul.
Re: Les dattes à Dattier
Dattier a écrit:1 : une question de bijectivité
Soit, et
tel que, pour
.
Trouver une CNS sur lespour que
soit bijective.
C'est assez facile :
Re: Les dattes à Dattier
Oui, mais reste à expliquer pourquoi c'est une CNS.
Re: Les dattes à Dattier
On peut procéder par récurrence sur  , en remarquant qu'il y a forcément
, en remarquant qu'il y a forcément  parmi les
parmi les  , on peut supposer que c'est
, on peut supposer que c'est  . Ensuite, les sommes sans
. Ensuite, les sommes sans 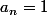 sont les nombres pairs entre
sont les nombres pairs entre  et
et 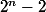 , on divise tous les
, on divise tous les  restants par
restants par  .
.
Re: Les dattes à Dattier
GaBuZoMeu a écrit:Ensuite, les sommes sanssont les nombres pairs...
Pourquoi sont-ils forcément pairs ?
Re: Les dattes à Dattier
Facile à voir. Je te donne une indication : l'ajout de  réalise une bijection entre l'ensemble des sommes sans
réalise une bijection entre l'ensemble des sommes sans 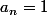 et l'ensemble des sommes avec.
et l'ensemble des sommes avec.
Re: Les dattes à Dattier
Ok, quand tu sauras résoudre l'énigme n'hésite pas à me biper (le chemin que j'ai en tête n'est pas celui-ci).
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

