Dattier a écrit:21 : Racine scindé Soient
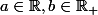
.
=x^3+3(1-a)x^2-(b+8a)x+2b(a-1))
est-il scindé dans

?
Mode bourrin : il suffit, pour montrer que

est scindé sur

, de montrer que le discriminant de

(par rapport à

) est positif ou nul. Ce discriminant, comme polynôme en

, est
*b^2\\ &\quad{} + (216*a^4 + 144*a^3 + 48*a^2 + 144*a + 216)*b\\ &\quad{} + 576*a^4 + 896*a^3 + 576*a^2\end{aligned})
Le discriminant de ce polynôme du troisième degré en

est
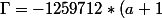^2 * (a - 1)^4 * (5*a^2 + 6*a + 5)^3)
Puisque

est négatif ou nul quel que soit

,

a toujours deux racines complexes conjuguées, éventuellement confondues. L'autre racine de

est donc du signe du produit des racines qui est
)
, donc cette autre racine de

est négative ou nulle, quel que soit

(le cas

ne pose pas de problème). En conclusion,

est positif ou nul et

est scindé sur

pour tout

et tout

positif ou nul.
est libre si et seulement si
est algébrique.

