Inégalité dans le plan
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 400
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 24 Mar 2013, 05:46
par MMu » 24 Mar 2013, 05:46
Soit

un sous-ensemble infini de points du plan ayant des coordonnées en nombres entiers positifs.
Montrer qu'il existe dans

deux points distincts
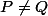
tels que

:zen:

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 27 Mar 2013, 14:56
par nuage » 27 Mar 2013, 14:56
MMu a écrit:Soit

un sous-ensemble infini de points du plan ayant des coordonnées en nombres entiers.
Montrer qu'il existe dans

deux points distincts
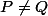
tels que

:zen:
Par exemple avec
\ |\ n\in \mathbb Z\})
:zen:
-
MMu
- Membre Relatif
- Messages: 400
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 28 Mar 2013, 03:11
par MMu » 28 Mar 2013, 03:11
nuage a écrit:Par exemple avec
\ |\ n\in \mathbb Z\})
:zen:
Mea culpa, (j'ai corrigé l'énoncé), j'ai oublié d'indiquer que les entiers sont positifs :triste:

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 28 Mar 2013, 18:18
par nuage » 28 Mar 2013, 18:18
Pour ceux qui veulent chercher :
-- la condition A infini est indispensable,
-- toute partie de

a un plus petit élément.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 28 Mar 2013, 19:53
par Matt_01 » 28 Mar 2013, 19:53
Pas très difficile quand on se rend compte visuellement pourquoi c'est vrai.
Par l'absurde, on peut par exemple montrer que dans le cas contraire, une des droites y=i possède une infinité de points de A et raisonner dessus.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 28 Mar 2013, 23:55
par nuage » 28 Mar 2013, 23:55
Matt_01 a écrit:Pas très difficile quand on se rend compte visuellement pourquoi c'est vrai.
Par l'absurde, on peut par exemple montrer que dans le cas contraire, une des droites y=i possède une infinité de points de A et raisonner dessus.
Un peu confus.
Et totalement faux si on le prend au pied de la lettre.
J'ai l'impression que tu dis le contraire de ce que tu penses.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 29 Mar 2013, 00:09
par Matt_01 » 29 Mar 2013, 00:09
nuage a écrit:Un peu confus.
Et totalement faux si on le prend au pied de la lettre.
J'ai l'impression que tu dis le contraire de ce que tu penses.
Dans le cas contraire où deux tels points n'existent pas, on aurait l'existence d'une telle droite. Non ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 29 Mar 2013, 00:15
par nuage » 29 Mar 2013, 00:15
On a deux tels points parce qu'il est possible qu'une telle droite existe.
Par exemple :
}\cup\{(n;0)\ |\ n\in\mathbb{N}\})
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 29 Mar 2013, 00:24
par Matt_01 » 29 Mar 2013, 00:24
En considérant l'inf des xi, disons xj, on se rend compte que y est borné dans le cas où deux tels points n'existent pas et donc une des droites y=ij'ai juste montré que (non p => p) pour montrer p.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités