Suites adjacentes
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 12:22
par Euler07 » 06 Déc 2010, 12:22
Salut

Exercice classique sur les suites adjacentes... Mais comment savoir la limite commune des deux ??? :doh:
Ps : Si c'est niveau MP (la réponse à ma question) alors dans ce cas je me couche

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2010, 12:54
par Ben314 » 06 Déc 2010, 12:54
La limite commune aux deux est 'e' (la base de l'exponentielle).
Une façon simple de le montrer : utiliser une des formules de taylors (avec reste) à l'ordre n pour la fonction t->exp(t) entre 0 et 1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 12:56
par Euler07 » 06 Déc 2010, 12:56
Ben314 a écrit:La limite commune aux deux est 'e' (la base de l'exponentielle).
Une façon simple de le montrer : utiliser une des formules de taylors (avec reste) à l'ordre n pour la fonction t->exp(t) entre 0 et 1.
Merci Ben314... Faut que j'attende encore un peu pour les développements limitées :dodo:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2010, 13:34
par Ben314 » 06 Déc 2010, 13:34
Pour un cas particulier simple comme là, tu peut le faire à la main complet en écrivant que :
e-1=int(exp(t),t=0..1)
puis tu fait des intégrations par parties en dérivant le exp(t) et en intégrant 1 qui devient t puis t²/2 puis...
Si tu le fait n fois, tu tombe à peu prés sur ce qu'il faut.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 13:36
par Euler07 » 06 Déc 2010, 13:36
Ok pas de souci ça marche bien ça ^^
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2010, 13:55
par Nightmare » 06 Déc 2010, 13:55
Salut !
Saurais-tu montrer, sans connaissance de l'exponentielle, que la suite
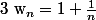^{n})
a la même limite que tes deux suites ?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 14:10
par Euler07 » 06 Déc 2010, 14:10
Bien sur Nightmare !!! Tu pose X=1/n et tu tombes sur une limite qui vaut 1 (en exposant) soit e^1
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 14:15
par Euler07 » 06 Déc 2010, 14:15
Cela vient de la limite ln(X+1)/X
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2010, 14:27
par Nightmare » 06 Déc 2010, 14:27
je me suis mal fait comprendre : indépendamment de savoir ce que vaut la limite de tes deux suites adjacentes et la mienne, pourrais-tu montrer néanmoins qu'elles ont toutes les trois la même limite? (C'est du même type que ton exercice quoi)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2010, 16:16
par Ben314 » 06 Déc 2010, 16:16
Euler 07 a écrit:Ok pas de souci ça marche bien ça ^^
En fait, j'ai tapé "à la va vite" (vu que j'avais cours) et je sais pas si tu a réussi à rectifier : si tu veut utiliser Taylors (sans le savoir...) tu part de :

et tu fait une intégration par partie avec
=1)
;
=e^t)
mais il faut prendre
=t-1)
(et pas
=t)
comme je l'avais dit) puis tu recommence (en prenant
^2)
comme primitive de

...
La méthode suggérée par Nightmare fonctionne aussi, mais c'est un peu plus "taupinal"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 16:30
par Euler07 » 06 Déc 2010, 16:30
Nightmare a écrit:je me suis mal fait comprendre : indépendamment de savoir ce que vaut la limite de tes deux suites adjacentes et la mienne, pourrais-tu montrer néanmoins qu'elles ont toutes les trois la même limite? (C'est du même type que ton exercice quoi)
Hum... Dans ce cas on recommence à montrer que an et wn sont adjacentes puis bn et wn non ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2010, 17:28
par Nightmare » 06 Déc 2010, 17:28
Bah, c'est pas vraiment possible d'avoir (an) et (wn) adjacentes en même temps que (bn) et (wn) étant donné que (an) et (bn) sont elles-même adjacentes !
Cela dit, (wn) n'est adjacente ni à (an) ni à (bn), ça n'empêche pas de pouvoir montrer qu'elles ont la même limite.
Edit : En fait, (wn) est bien adjacente à (bn), à prouver bien entendu !
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 17:35
par Euler07 » 06 Déc 2010, 17:35
Nightmare a écrit:Bah, c'est pas vraiment possible d'avoir (an) et (wn) adjacentes en même temps que (bn) et (wn) étant donné que (an) et (bn) sont elles-même adjacentes !
Cela dit, (wn) n'est adjacente ni à (an) ni à (bn), ça n'empêche pas de pouvoir montrer qu'elles ont la même limite.
Edit : En fait, (wn) est bien adjacente à (bn), à prouver bien entendu !
Explication ? Wn est bien adjacente à bn ?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 06 Déc 2010, 17:36
par Euler07 » 06 Déc 2010, 17:36
Sinon je veux bien le prouvait
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Déc 2010, 17:53
par Nightmare » 06 Déc 2010, 17:53
(un) est croissante et (vn) décroissante. Comment voudrais-tu que (wn) soit adjacente en même temps à (un) et à (vn) ? Il faudrait qu'elle soit en même temps décroissante (pour être adjacente à (un)) et croissante (pour être adjacente à (vn)).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités

