Tu dis que c'est inévitable de passer par 2^u, si j'ai bien compris ton raisonnement, mais pourquoi ? Ce n'est pas évident du tout! Ce n'est pas en tout cas ton équation (1) qui le dit.
Non, je ne sais pas que toutes les suites de Collatz passent par 2^x. Je sais seulement que toutes celles que j'ai pu regarder le font, ce qui est loin d'en faire une généralité.
Pour le tableau que j'ai critiqué, il faudrait soit le retoucher, soit l'abandonner. Si tu laisses en l'état, c'est sûr qu'on ne te lira pas plus loin.
Pour u(n2^x)=un+x Ok vu.
Arbre des suites de Syracuse
80 messages
- Page 4 sur 4 - 1, 2, 3, 4
par syrac » 18 Jan 2015, 15:44
nodjim a écrit:Tu dis que c'est inévitable de passer par 2^u, si j'ai bien compris ton raisonnement, mais pourquoi ? Ce n'est pas évident du tout! Ce n'est pas en tout cas ton équation (1) qui le dit.
Relis le bas de la page 1.
nodjim a écrit:Non, je ne sais pas que toutes les suites de Collatz passent par 2^x. Je sais seulement que toutes celles que j'ai pu regarder le font, ce qui est loin d'en faire une généralité.
Alors essaie de le démontrer.
EDIT : c'est en fait très simple. Si tu es d'accord que toutes les suites se terminent par la boucle 4, 2, 1, ça veut dire qu'avant 4 il y a eu au moins 8, égal à 2^3. CQFD.
nodjim a écrit:Pour le tableau que j'ai critiqué, il faudrait soit le retoucher, soit l'abandonner. Si tu laisses en l'état, c'est sûr qu'on ne te lira pas plus loin.
On ne peut pas jeter une théorie aux oubliettes pour un point de détail aussi insignifiant.
par syrac » 18 Jan 2015, 15:59
Je corrige ma dernière phrase : "On ne peut pas jeter une théorie aux oubliettes pour un point de détail aussi insignifiant. Ceux qui s'arrêtent à lui n'en retireront de toute façon aucun enseignement, parce qu'ils ne s'efforcent pas de comprendre mais de discréditer".
par syrac » 18 Jan 2015, 19:19
Test de différentes valeurs de k dans le problème 3n+k avec l'équation unificatrice :
3n+3 :
n=1 -> 1, 3, 6, 6, ...
n=3 -> 3,6, 6, ...
n=5 -> 5, 9, 15, 24, 6, 6, ...
n=7 -> 7, 12, 6, 6, ...
n=9 -> 9, 15, 24, 6, 6, ...
n=11 -> 11, 18, 15, 24, 6, 6, ...
Avec n = 1235 on a : 1235, 1854, 1392, 132, 51, 78, 60, 24, 6, 6
=> Si ces résultats se confirment, une arborescence est possible avec 3n+3
(3n+5 a été testé ci-dessus. Pas d'arborescence possible.)
3n+7 :
n=1 -> 1, 5, 11, 20, 11, 20, 11, 20, ...
n=3 -> 3, 8, 5, 11, 20, 11, 20, 11, 20, ...
n=5 -> 5, 11, 20, 11, 20, 11, 20, ...
n=7 -> 7, 14, 14, ...
n=9 -> 9, 17, 29, 47, 74, 59, 92, 38, 32, 5, 11, 20, 11, 20, 11, 20, ...
n=11 -> 11, 20, 11, 20, 11, 20, ...
=> Pas d'arborescence possible avec 3n+7
3n+9 :
n=1 -> 1, 6, 9, 18, 18, ...
n=3 -> 3, 9, 18, 18, ...
n=5 -> 5, 12, 9, 18, 18, ...
n=7 -> 7, 15, 27, 45, 72, 18, 18, ...
n=9 -> 9, 18, 18, ...
n=11 -> 11, 21, 36, 18, 18, ...
Avec n = 1235 on a : 1235, 857, 2790, 2097, 3150, ..., 4392, 828, 315, 477, 720, 72, 18, 18
=> Si ces résultats se confirment, une arborescence est possible avec 3n+9
3n+11 :
n=1 -> 1, 7, 16, 7, 16, 7, 16, ...
n=3 -> 3, 10, 13, 25, 43, 70, 58, 49, 79, 124, 52, 25, 43, 70, 58, 49, 79, 124, 52, ... -> boucle 25, 43, 70, 58, 49, 79, 124, 52
=> Pas d'arborescence possible avec 3n+11
3n+13 :
n=1 -> 1, 8, 8, ...
n=3 -> 3, 11, 23, 41, 68, 32, 8, 8, ...
n=5 -> 5, 14, 17, 32, 8, 8, ...
n=7 -> 7, 17, 32, 8, 8, ...
n=9 -> 9, 20, 14, 17, 32, 8, 8, ...
n=11 -> 11, 23, 41, 68, 32, 8, 8, ...
Mais avec n = 1235 on a : 1235, 859, 2795, 4199, 6305, ..., 6344, 1196, 455, 689, 1040, 104, 26, 26
=> Pas d'arborescence possible avec 3n+13
3n+15 :
n=1 -> 1, 9, 21, 39, 66, 57, 93, 147, 228, 93, 147, 228, 93, 147, 228, ... -> boucle 93, 147, 228
n=3 -> 3, 12, 12, ...
n=5 -> 5, 15, 30, 30, ...
=> Pas d'arborescence possible avec 3n+15
3n+17 :
n=1 -> 1, 10, 16, 10, 16, 10 16, ...
n=3 -> 3, 13, 28, 19, 37, 64, 10, 16, 10, 16, 10, 16, ...
=> Pas d'arborescence possible avec 3n+17
3n+19 :
n=1 -> 1, 11, 26, 29, 53, 89, 143, 224, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> boucle 20, 17, 35, 62, 56
n=3 -> 3, 14, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> idem
=> Pas d'arborescence possible avec 3n+19
3n+21 :
n=1 -> 1, 12, 15, 33, 60, 33, 60, 33, 60, ...
n=3 -> 3, 14, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> boucle 20, 17, 35, 62, 56
=> Pas d'arborescence possible avec 3n+21
Enfin, puisqu'une arborescence semble possible avec 3n+3 et 3n+9, j'ai voulu tester 3n+27 :
3n+27 :
n=1 -> 1, 15, 36, 27, 54, 54, ...
n=3 -> 3, 18, 27, 54, 54, ...
n=5 -> 5, 21, 45, 81, 135, 216, 54, 54, ...
n=7 -> 7, 24, 18, 27, 54, 54, ...
n=9 -> 9, 27, 54, 54, ...
n=11 -> 11, 30, 36, 27, 54, 54, ...
Avec n = 1235 on a : 1235, 1866, 1413, 2133, 3213, 4833, 7263, 10908, 4104, 783, 1188, 459, 702, 540, 216, 54, 54
=> Si ces résultats se confirment, une arborescence est possible avec 3n+27
Testons 3n+45 (9*5) :
n=1 -> 1, 24, 27, 63, 117, 198, 171, 279, 441, 684, 279, 441, 684, 279, 441, 684, ... -> boucle 279, 441, 684
n=3 -> 3, 27, 63, 117, 198, 171, 279, 441, 684, 279, 441, 684, ... -> idem
=> Pas d'arborescence possible avec 3n+45
Testons 3n+81 (9^2) :
n=1 -> 1, 42, 72, 54, 81, 162, 162, ...
n=3 -> 3, 45, 108, 81, 162, 162, ...
n=5 -> 5, 48, 45, 108, 81, 162, 162, ...
n=7 -> 7, 51, 117, 216, 81, 162, 162, ...
n=9 -> 9, 54, 81, 162, 162, ...
n=11 -> 11, 57, 126, 135, 243, 405, 648, 162, 162, ..
Avec n = 1235 on a : 1235, 1893, 2880, 108, 81, 162, 162, ...
=> Si ces résultats se confirment, une arborescence est possible avec 3n+81
Résultat très intéressant : il semble en effet qu'on puisse créer un arbre avec 3n+1, 3n+3, 3n+9, 3n+27, 3n+81, soit 3n+3^x, avec x >= 0.
3n+3 :
n=1 -> 1, 3, 6, 6, ...
n=3 -> 3,6, 6, ...
n=5 -> 5, 9, 15, 24, 6, 6, ...
n=7 -> 7, 12, 6, 6, ...
n=9 -> 9, 15, 24, 6, 6, ...
n=11 -> 11, 18, 15, 24, 6, 6, ...
Avec n = 1235 on a : 1235, 1854, 1392, 132, 51, 78, 60, 24, 6, 6
=> Si ces résultats se confirment, une arborescence est possible avec 3n+3
(3n+5 a été testé ci-dessus. Pas d'arborescence possible.)
3n+7 :
n=1 -> 1, 5, 11, 20, 11, 20, 11, 20, ...
n=3 -> 3, 8, 5, 11, 20, 11, 20, 11, 20, ...
n=5 -> 5, 11, 20, 11, 20, 11, 20, ...
n=7 -> 7, 14, 14, ...
n=9 -> 9, 17, 29, 47, 74, 59, 92, 38, 32, 5, 11, 20, 11, 20, 11, 20, ...
n=11 -> 11, 20, 11, 20, 11, 20, ...
=> Pas d'arborescence possible avec 3n+7
3n+9 :
n=1 -> 1, 6, 9, 18, 18, ...
n=3 -> 3, 9, 18, 18, ...
n=5 -> 5, 12, 9, 18, 18, ...
n=7 -> 7, 15, 27, 45, 72, 18, 18, ...
n=9 -> 9, 18, 18, ...
n=11 -> 11, 21, 36, 18, 18, ...
Avec n = 1235 on a : 1235, 857, 2790, 2097, 3150, ..., 4392, 828, 315, 477, 720, 72, 18, 18
=> Si ces résultats se confirment, une arborescence est possible avec 3n+9
3n+11 :
n=1 -> 1, 7, 16, 7, 16, 7, 16, ...
n=3 -> 3, 10, 13, 25, 43, 70, 58, 49, 79, 124, 52, 25, 43, 70, 58, 49, 79, 124, 52, ... -> boucle 25, 43, 70, 58, 49, 79, 124, 52
=> Pas d'arborescence possible avec 3n+11
3n+13 :
n=1 -> 1, 8, 8, ...
n=3 -> 3, 11, 23, 41, 68, 32, 8, 8, ...
n=5 -> 5, 14, 17, 32, 8, 8, ...
n=7 -> 7, 17, 32, 8, 8, ...
n=9 -> 9, 20, 14, 17, 32, 8, 8, ...
n=11 -> 11, 23, 41, 68, 32, 8, 8, ...
Mais avec n = 1235 on a : 1235, 859, 2795, 4199, 6305, ..., 6344, 1196, 455, 689, 1040, 104, 26, 26
=> Pas d'arborescence possible avec 3n+13
3n+15 :
n=1 -> 1, 9, 21, 39, 66, 57, 93, 147, 228, 93, 147, 228, 93, 147, 228, ... -> boucle 93, 147, 228
n=3 -> 3, 12, 12, ...
n=5 -> 5, 15, 30, 30, ...
=> Pas d'arborescence possible avec 3n+15
3n+17 :
n=1 -> 1, 10, 16, 10, 16, 10 16, ...
n=3 -> 3, 13, 28, 19, 37, 64, 10, 16, 10, 16, 10, 16, ...
=> Pas d'arborescence possible avec 3n+17
3n+19 :
n=1 -> 1, 11, 26, 29, 53, 89, 143, 224, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> boucle 20, 17, 35, 62, 56
n=3 -> 3, 14, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> idem
=> Pas d'arborescence possible avec 3n+19
3n+21 :
n=1 -> 1, 12, 15, 33, 60, 33, 60, 33, 60, ...
n=3 -> 3, 14, 20, 17, 35, 62, 56, 20, 17, 35, 62, 56, ... -> boucle 20, 17, 35, 62, 56
=> Pas d'arborescence possible avec 3n+21
Enfin, puisqu'une arborescence semble possible avec 3n+3 et 3n+9, j'ai voulu tester 3n+27 :
3n+27 :
n=1 -> 1, 15, 36, 27, 54, 54, ...
n=3 -> 3, 18, 27, 54, 54, ...
n=5 -> 5, 21, 45, 81, 135, 216, 54, 54, ...
n=7 -> 7, 24, 18, 27, 54, 54, ...
n=9 -> 9, 27, 54, 54, ...
n=11 -> 11, 30, 36, 27, 54, 54, ...
Avec n = 1235 on a : 1235, 1866, 1413, 2133, 3213, 4833, 7263, 10908, 4104, 783, 1188, 459, 702, 540, 216, 54, 54
=> Si ces résultats se confirment, une arborescence est possible avec 3n+27
Testons 3n+45 (9*5) :
n=1 -> 1, 24, 27, 63, 117, 198, 171, 279, 441, 684, 279, 441, 684, 279, 441, 684, ... -> boucle 279, 441, 684
n=3 -> 3, 27, 63, 117, 198, 171, 279, 441, 684, 279, 441, 684, ... -> idem
=> Pas d'arborescence possible avec 3n+45
Testons 3n+81 (9^2) :
n=1 -> 1, 42, 72, 54, 81, 162, 162, ...
n=3 -> 3, 45, 108, 81, 162, 162, ...
n=5 -> 5, 48, 45, 108, 81, 162, 162, ...
n=7 -> 7, 51, 117, 216, 81, 162, 162, ...
n=9 -> 9, 54, 81, 162, 162, ...
n=11 -> 11, 57, 126, 135, 243, 405, 648, 162, 162, ..
Avec n = 1235 on a : 1235, 1893, 2880, 108, 81, 162, 162, ...
=> Si ces résultats se confirment, une arborescence est possible avec 3n+81
Résultat très intéressant : il semble en effet qu'on puisse créer un arbre avec 3n+1, 3n+3, 3n+9, 3n+27, 3n+81, soit 3n+3^x, avec x >= 0.
par nodjim » 18 Jan 2015, 20:00
Je connais déja et ça s'explique très bien. Les 3n+3^k ont d'ailleurs fait l'objet d'une question d'énigme à part entière.
J'ai des réponses en retard. Pour le tableau, s'il présente un intérêt tu le gardes, mais il faut le corriger, tu as bien vu qu'il ne marche pas: Pour utiliser la 1ère colonne, tu as compris qu'on ne pouvait pas le limiter.
Tu signales "pas d'arborescence" pour de nombreux cas, or il me semble que l'arborescence est toujours possible, mais que pour certains cas, elle est multiple. Mais bon c'est une question de vocabulaire. Sinon, on a bien entendu les mêmes résultats que si tu utilisais la suite Collatz. Quand tu dis arborescence ou pas, je vois bien que tu as fait le test pour un nombre réduit de cas. Si je te propose 3n+49097, que réponds tu ?
J'ai des réponses en retard. Pour le tableau, s'il présente un intérêt tu le gardes, mais il faut le corriger, tu as bien vu qu'il ne marche pas: Pour utiliser la 1ère colonne, tu as compris qu'on ne pouvait pas le limiter.
Tu signales "pas d'arborescence" pour de nombreux cas, or il me semble que l'arborescence est toujours possible, mais que pour certains cas, elle est multiple. Mais bon c'est une question de vocabulaire. Sinon, on a bien entendu les mêmes résultats que si tu utilisais la suite Collatz. Quand tu dis arborescence ou pas, je vois bien que tu as fait le test pour un nombre réduit de cas. Si je te propose 3n+49097, que réponds tu ?
par nodjim » 18 Jan 2015, 20:04
Noté au passage:
"EDIT : c'est en fait très simple. Si tu es d'accord que toutes les suites se terminent par la boucle 4, 2, 1, ça veut dire qu'avant 4 il y a eu au moins 8, égal à 2^3. CQFD."
Ben, non, je ne suis pas d'accord pour dire que toutes les suites se terminent dans la boucle 4,2,1. Je le crois, mais je n'en ai pas la preuve. C'est ça qu'on cherche depuis la présentation de cette conjecture.
"EDIT : c'est en fait très simple. Si tu es d'accord que toutes les suites se terminent par la boucle 4, 2, 1, ça veut dire qu'avant 4 il y a eu au moins 8, égal à 2^3. CQFD."
Ben, non, je ne suis pas d'accord pour dire que toutes les suites se terminent dans la boucle 4,2,1. Je le crois, mais je n'en ai pas la preuve. C'est ça qu'on cherche depuis la présentation de cette conjecture.
par syrac » 18 Jan 2015, 20:11
nodjim a écrit:Si je te propose 3n+49097, que réponds tu ?
Les suites sont trop longues et complexes pour y rechercher une boucle. De plus, Mathematica ne trouve pas de succession d'entiers identiques, ce qui pourtant indiquerait la présence d'une racine. Enfin, 49097 est égal à 29*1693, ce qui n'est pas une puissance de 3. J'en déduis qu'on ne peut pas former un arbre sur 3n+49097.
par syrac » 18 Jan 2015, 20:32
nodjim a écrit:J'ai des réponses en retard. Pour le tableau, s'il présente un intérêt tu le gardes, mais il faut le corriger, tu as bien vu qu'il ne marche pas: Pour utiliser la 1ère colonne, tu as compris qu'on ne pouvait pas le limiter.
Avec un peu de bonne volonté on se sort de toutes les situations qui à l'origine semblaient inextricables. Tu construits un tableau de 2 colonnes. La colonne de gauche contient les entiers de 1 à 100, et la colonne de droite contient, dans l'ordre, les entiers suivants :
2,2,5,2,8,5,11,2,14,8,17,5,20,11,23,2,26,14,29,8,32,17,35,5,38,20,41,11,44,23,47,2,50,26,53,14,56,29,59,8,62,32,65,17,68,35,71,5,74,38,77,20,80,41,83,11,86,44,89,23,92,47,95,2,98,50,101,26,104,53,107,14,110,56,113,29,116,59,119,8,122,62,125,32,128,65,131,17,134,68,137,35,140,71,143,5,146,74,149,38.
Si tu suis la procédure indiquée tu tomberas nécessairement sur 2 au bout d'un certain nombre d'étapes.
nodjim a écrit:Tu signales "pas d'arborescence" pour de nombreux cas, or il me semble que l'arborescence est toujours possible, mais que pour certains cas, elle est multiple. Mais bon c'est une question de vocabulaire. Sinon, on a bien entendu les mêmes résultats que si tu utilisais la suite Collatz.
Je ne vois pas à quoi peut ressembler une arborescence multiple. Tu as un exemple ?
Non, créer une arborescence avec l'algorithme de Collatz est IMPOSSIBLE ! Avant de contester je te suggère d'essayer et de me démontrer ce faisant le contraire. Sinon la critique est trop aisée pour convaincre.
par nodjim » 18 Jan 2015, 20:55
Pour cette remarque:
2,2,5,2,8,5,11,2,14,8,17,5,20,11,23,2,26,14,29,8,3 2,17,35,5,38,20,41,11,44,23,47,2,50,26,53,14,56,29 ,59,8,62,32,65,17,68,35,71,5,74,38,77,20,80,41,83, 11,86,44,89,23,92,47,95,2,98,50,101,26,104,53,107, 14,110,56,113,29,116,59,119,8,122,62,125,32,128,65 ,131,17,134,68,137,35,140,71,143,5,146,74,149,38.
Si tu suis la procédure indiquée tu tomberas nécessairement sur 2 au bout d'un certain nombre d'étapes.
Je suis d'accord avec toi. Cependant 2 choses me chagrinent:
Dans ta démonstration, tu disais qu'il fallait se servir des nombres du tableau de la 1ère colonne pour suivre la suite. Or il y a bien des nombres >100 comme successeurs. Comment fais tu pour te servir des nombres de la 1ère colonne qui s'arrête à 100 ?
Les 100 premiers aboutissent à 2. Il en est de même pour tous les nombres < 10^18.
Mais es tu certain que ce sera pareil pour les autres nombres ?
Pour moi l'arborescence, c'est partir d'une souche et remonter la suite. Note bien tout de même que 2 n'est pas un final, mais une boucle sur elle même, que tu devrais tout de même représenter pour l'exactitude de la démo, car l'algorithme ne s'arrête pas lui.
Le fait qu'il existe des boucles plus longues que l'unité n'empêche pas de créer une arborescence: des nombres d'une boucle donnée sont origine d'une arborescence.
Amorce de l'arborescence de Collatz:
1<---2<---4<----8<----16<-----32<-----
....................................^------5<-----10<-----20<-----40<-----80<----
............................................................^-----3............^------13<-----
Bon maintenant, il y a peut être un problème de vocabulaire sur ce que tu nommes arborescence. A préciser si possible.
Une autre remarque en passant:
Tu peux encore raccourcir ton équation (1) en te passant directement des nombres pairs:
ns=1/2^v (3n/2^u+1) ou 2^v permet d'éliminer les nombres pairs.
2,2,5,2,8,5,11,2,14,8,17,5,20,11,23,2,26,14,29,8,3 2,17,35,5,38,20,41,11,44,23,47,2,50,26,53,14,56,29 ,59,8,62,32,65,17,68,35,71,5,74,38,77,20,80,41,83, 11,86,44,89,23,92,47,95,2,98,50,101,26,104,53,107, 14,110,56,113,29,116,59,119,8,122,62,125,32,128,65 ,131,17,134,68,137,35,140,71,143,5,146,74,149,38.
Si tu suis la procédure indiquée tu tomberas nécessairement sur 2 au bout d'un certain nombre d'étapes.
Je suis d'accord avec toi. Cependant 2 choses me chagrinent:
Dans ta démonstration, tu disais qu'il fallait se servir des nombres du tableau de la 1ère colonne pour suivre la suite. Or il y a bien des nombres >100 comme successeurs. Comment fais tu pour te servir des nombres de la 1ère colonne qui s'arrête à 100 ?
Les 100 premiers aboutissent à 2. Il en est de même pour tous les nombres < 10^18.
Mais es tu certain que ce sera pareil pour les autres nombres ?
Pour moi l'arborescence, c'est partir d'une souche et remonter la suite. Note bien tout de même que 2 n'est pas un final, mais une boucle sur elle même, que tu devrais tout de même représenter pour l'exactitude de la démo, car l'algorithme ne s'arrête pas lui.
Le fait qu'il existe des boucles plus longues que l'unité n'empêche pas de créer une arborescence: des nombres d'une boucle donnée sont origine d'une arborescence.
Amorce de l'arborescence de Collatz:
1<---2<---4<----8<----16<-----32<-----
....................................^------5<-----10<-----20<-----40<-----80<----
............................................................^-----3............^------13<-----
Bon maintenant, il y a peut être un problème de vocabulaire sur ce que tu nommes arborescence. A préciser si possible.
Une autre remarque en passant:
Tu peux encore raccourcir ton équation (1) en te passant directement des nombres pairs:
ns=1/2^v (3n/2^u+1) ou 2^v permet d'éliminer les nombres pairs.
par syrac » 18 Jan 2015, 21:51
nodjim a écrit:Dans ta démonstration, tu disais qu'il fallait se servir des nombres du tableau de la 1ère colonne pour suivre la suite. Or il y a bien des nombres >100 comme successeurs. Comment fais tu pour te servir des nombres de la 1ère colonne qui s'arrête à 100 ?
Juste avant le graphe de la page 3, donc à la fin de la page 2, je dis ceci : "Votre graphe vérifie la conjecture si tous ses chemins convergent sur 2. Voici celui obtenu en prenant successivement les 25 premiers entiers comme valeur initiale".
Exemples :
syracuse(23) = 23, 35, 53, 80, 8, 2
syracuse(24) = 24, 5, 8, 2
syracuse(25) = 25, 38, 29, 44, 17, 26, 20, 8, 2
Il faut prendre des entiers dont la suite ne contient aucun terme > 100, afin de vérifier que le graphe obtenu converge bien sur 2. Ça me semble assez évident. Pour les entiers plus grands tu utilises ta calculette ou ton ordinateur.
nodjim a écrit:Mais es tu certain que ce sera pareil pour les autres nombres ?
Non. Je ne vais pas passer les 300 prochaines années à tester tous les entiers.
nodjim a écrit:Amorce de l'arborescence de Collatz:
1<---2<---4<----8<----16<-----32<-----
....................................^------5<-----10<-----20<-----40<-----80<----
............................................................^-----3............^------13<-----
Réveilles-moi quand tu auras quelque chose qui ressemble à une arborescence !
nodjim a écrit:Une autre remarque en passant:
Tu peux encore raccourcir ton équation (1) en te passant directement des nombres pairs:
ns=1/2^v (3n/2^u+1) ou 2^v permet d'éliminer les nombres pairs.
Si l'arbre ne contenait aucun entier pair il ne ressemblerait plus à rien.
par syrac » 19 Jan 2015, 01:24
[CENTER]Quelques arbres de la forêt[/CENTER]
Voici un petit extrait des arbres 3n+1 à +81, dans la plage d'entiers (3,70). Quelques noeuds se chevauchent horizontalement, mais la place manque en largeur. Ces images servent uniquement à se faire une idée de leurs têtes respectives. Les noeuds orangés sont ceux qui n'ont pas de prédécesseur ; ce sont donc les feuilles de l'arbre.
Arbre 3n+1
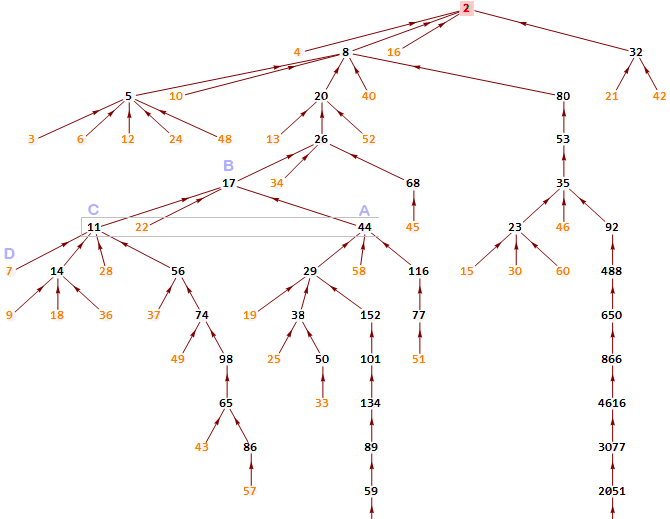
Arbre 3n+3
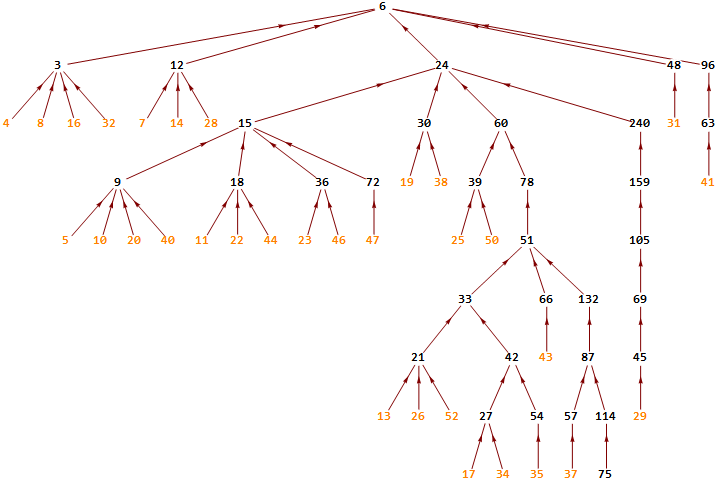
Arbre 3n+9
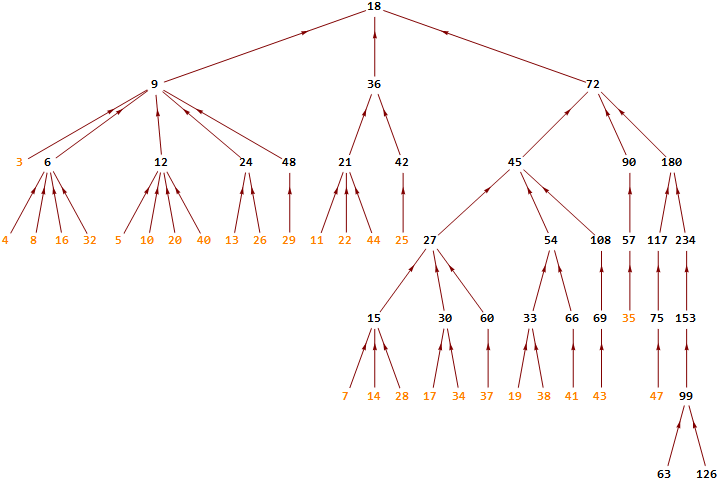
Arbre 3n+27
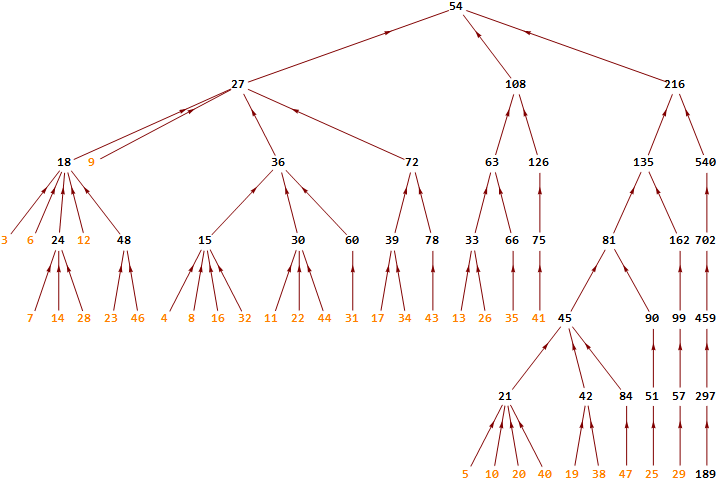
Arbre 3n+81
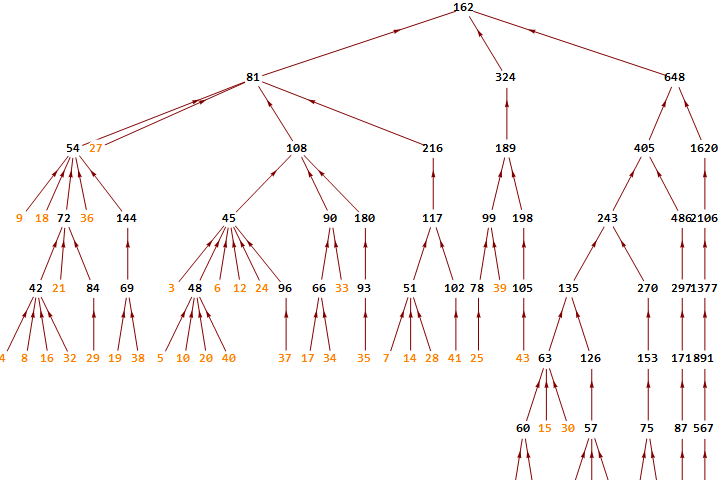
Vous pouvez faire péter le champagne, les gars, parce que c'est une première mondiale ! :we:
Voici un petit extrait des arbres 3n+1 à +81, dans la plage d'entiers (3,70). Quelques noeuds se chevauchent horizontalement, mais la place manque en largeur. Ces images servent uniquement à se faire une idée de leurs têtes respectives. Les noeuds orangés sont ceux qui n'ont pas de prédécesseur ; ce sont donc les feuilles de l'arbre.
Arbre 3n+1
Arbre 3n+3
Arbre 3n+9
Arbre 3n+27
Arbre 3n+81
Vous pouvez faire péter le champagne, les gars, parce que c'est une première mondiale ! :we:
par syrac » 19 Jan 2015, 15:36
Voici comment interpréter un chemin en fonction de l'algorithme de Collatz. Je prends pour exemple la feuille 15 en bas à droite de l'arbre 3n+81 ci-dessus.
collatz81(15) = 15, 126, 63, 270, 135, 486, 243, 810, 405, 1296, 648, 324, 1622.
Son chemin dans l'arbre est pour sa part:
syracuse81(15) = 15, 63, 135, 243, 405, 648, 162.
Dans la suite collatz81(15), 15 est suivi de 126 puis de 63. Dans la suite syracuse81(15), le groupe 63, 126, 252, 504, , succède au groupe 15, 30, 60, 120, , si bien que 15 ne passe pas par 126 pour atteindre 63. On peut faire la même remarque à propos de 63 lui-même, qui na pas à passer par 270 pour atteindre 135 puisque 270 nest pas son successeur mais un membre du groupe ;)135.
Dans la suite de Collatz on trouve une succession dentiers, alors que la suite de syracuse produit une succession de nuds. Il n'y a pas de différence, autre que de positionnement, entre l'algorithme de Collatz et celui de syracuse (avec l'équation unificatrice, ou algorithme simplifié). Et c'est justement ce positionnement différent qui permet de construire l'arbre.
collatz81(15) = 15, 126, 63, 270, 135, 486, 243, 810, 405, 1296, 648, 324, 1622.
Son chemin dans l'arbre est pour sa part:
syracuse81(15) = 15, 63, 135, 243, 405, 648, 162.
Dans la suite collatz81(15), 15 est suivi de 126 puis de 63. Dans la suite syracuse81(15), le groupe 63, 126, 252, 504, , succède au groupe 15, 30, 60, 120, , si bien que 15 ne passe pas par 126 pour atteindre 63. On peut faire la même remarque à propos de 63 lui-même, qui na pas à passer par 270 pour atteindre 135 puisque 270 nest pas son successeur mais un membre du groupe ;)135.
Dans la suite de Collatz on trouve une succession dentiers, alors que la suite de syracuse produit une succession de nuds. Il n'y a pas de différence, autre que de positionnement, entre l'algorithme de Collatz et celui de syracuse (avec l'équation unificatrice, ou algorithme simplifié). Et c'est justement ce positionnement différent qui permet de construire l'arbre.
par nodjim » 19 Jan 2015, 19:37
L'explication de la ressemblance entre 3n+1 et 3n+3^k. k entier.
Bonne lecture.
n impair----->3n+3^k qui est divisible par 3, caractère conservé quand on divise par 2. Le résultat impair peut s'écrire 3m.
3m---->3*3m+3^k est divisible par 9 si k>=2. divisé par 2 (une ou plusieurs fois) ne change pas la divisibilité par 9. On écrira le résultat impair 9p.
9p---->3*9p+3^k résultat divisible par 27 si k>=3.
etc, jusqu'à avoir un résultat sous la forme (n*3^k).
3*(n*3^k)+3^k=3^k(3n+1)
C'est fini, car alors tous les résultats suivants sont des multiples par 3^k de la suite de Syracuse.
Bonne lecture.
n impair----->3n+3^k qui est divisible par 3, caractère conservé quand on divise par 2. Le résultat impair peut s'écrire 3m.
3m---->3*3m+3^k est divisible par 9 si k>=2. divisé par 2 (une ou plusieurs fois) ne change pas la divisibilité par 9. On écrira le résultat impair 9p.
9p---->3*9p+3^k résultat divisible par 27 si k>=3.
etc, jusqu'à avoir un résultat sous la forme (n*3^k).
3*(n*3^k)+3^k=3^k(3n+1)
C'est fini, car alors tous les résultats suivants sont des multiples par 3^k de la suite de Syracuse.
par nodjim » 20 Jan 2015, 20:49
Euh... dans la suite de Collatz ou assimilée (quand on remplace 3^k^ par 1) on divise par 2, pas par 3.
par syrac » 24 Jan 2015, 20:30
[CENTER]A l'attention des utilisateurs de Mathematica[/CENTER]
J'ai ajouté à l'archive contenant le bloc-notes destiné à effectuer tous les calculs relatifs à mon papier, un autre bloc-notes destiné à construire les arbres 3n+3^k.
Vous pouvez la télécharger ici
J'ai ajouté à l'archive contenant le bloc-notes destiné à effectuer tous les calculs relatifs à mon papier, un autre bloc-notes destiné à construire les arbres 3n+3^k.
Vous pouvez la télécharger ici
80 messages
- Page 4 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :