Suites-parité
18 messages
- Page 1 sur 1
suites-parité
Bonjour
en étudiant la suite récurrente suivante :
U(0)=3
u(n+1)=(1/4)[(u(n))^2+6u(n)+1] pour n entier naturel
je me suis bloqué devant le fait de montrer que :
tous les termes de cette suite sont des nombres impairs
se terminant par 3 ou par 7?
cette suite n'est pas parvenue par hasard mais suite à une question
que je me suis posé et que je citerai plus tard pour enrichir le sujet.
Merci
en étudiant la suite récurrente suivante :
U(0)=3
u(n+1)=(1/4)[(u(n))^2+6u(n)+1] pour n entier naturel
je me suis bloqué devant le fait de montrer que :
tous les termes de cette suite sont des nombres impairs
se terminant par 3 ou par 7?
cette suite n'est pas parvenue par hasard mais suite à une question
que je me suis posé et que je citerai plus tard pour enrichir le sujet.
Merci
Re: suites-parité
Bonjour,
Un nombre impair est un nombre qui s'écrit de la forme avec
avec  un entier relatif.
un entier relatif.
Il faut ensuite faire une démonstration par récurrence.
Pour montrer qu'ils se terminent tous par 3 ou par 7, il faut prendre le nombre modulo 10.
modulo 10.
Un nombre impair est un nombre qui s'écrit de la forme
Il faut ensuite faire une démonstration par récurrence.
Pour montrer qu'ils se terminent tous par 3 ou par 7, il faut prendre le nombre
Re: suites-parité
Re: suites-parité
merci beaucoup pour votre indulgence et votre patience . C'est la première fois que je participe
à un forum.
j'ai utilisé la démonstration par récurrence mais je bloque devant
u(n)= 2k+1 ............u(n+1)=(k+1)^2+1 impair ? comment ?
à un forum.
j'ai utilisé la démonstration par récurrence mais je bloque devant
u(n)= 2k+1 ............u(n+1)=(k+1)^2+1 impair ? comment ?
Re: suites-parité
je vous remercie pour votre réponse .Je vous demande excuse si j'abuse un peu de votre
temps .
j'ai essayé comme vous l'avez signalé mais ça bloque
u(n)=2k+1 ..........> u(n+1) = (k+1)^2+1 dont la parité reste à démontrer!
peut etre j'ai mal vu !
temps .
j'ai essayé comme vous l'avez signalé mais ça bloque
u(n)=2k+1 ..........> u(n+1) = (k+1)^2+1 dont la parité reste à démontrer!
peut etre j'ai mal vu !
Re: suites-parité
Bonjour,
Effectivement, j'ai eu le même soucis:
Mais d'après ton énoncé, nous avons:
"tous les termes de cette suite sont des nombres impairs se terminant par 3 ou par 7?"
il n y a pas de saut de ligne (donc prendre directement à la récurrence en posant et démontrer que
et démontrer que  s'écrit sous la forme
s'écrit sous la forme  et vice versa et la parité est immédiate car ce n'est pas demandé de la démontrer à part).
et vice versa et la parité est immédiate car ce n'est pas demandé de la démontrer à part).
Effectivement, j'ai eu le même soucis:
Mais d'après ton énoncé, nous avons:
"tous les termes de cette suite sont des nombres impairs se terminant par 3 ou par 7?"
il n y a pas de saut de ligne (donc prendre directement à la récurrence en posant
Re: suites-parité
Pourquoi 20?
Laisse 10 car on est en base 10. et nous sommes intéressés par le chiffre unité qui doit être 3 ou 7.
Laisse 10 car on est en base 10. et nous sommes intéressés par le chiffre unité qui doit être 3 ou 7.
Re: suites-parité
bonjour pour un texte plus lisible!
comme je l'ai déjà dit au début , la question de parité est venue au cours
de l'étude d'une suite que j'ai proposé et que je l'appellerai par la suite
suite de digischool1(dS1)qui est :
 +"Somme des nombres impairs
+"Somme des nombres impairs ;pour n entier naturel
;pour n entier naturel
En effet les termes de cette suite sont impairs (et qu'il fallait démontrer) et en supposons ainsi ,
 =u_{n}+[((u_{n}-1)/2)+1]^2=(\frac{1}{4})[(u_{n})^2+6u_{n}+1])
qui est la formule que j'ai donné au début.
une autre suite de même nature
(dS2) "somme des nombres pairs
"somme des nombres pairs  "
"
pour celle ci il est facile de montrer que
[(v_{n})^2+4v_{n}-1]) et que tous ces termes(
et que tous ces termes(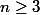 ) se terminent par 1
) se terminent par 1
alors une autre question que je propose :
Est -il possible de ramener les termes de ces suites sous la forme ?
?
comme je l'ai déjà dit au début , la question de parité est venue au cours
de l'étude d'une suite que j'ai proposé et que je l'appellerai par la suite
suite de digischool1(dS1)qui est :
En effet les termes de cette suite sont impairs (et qu'il fallait démontrer) et en supposons ainsi ,
qui est la formule que j'ai donné au début.
une autre suite de même nature
(dS2)
pour celle ci il est facile de montrer que
alors une autre question que je propose :
Est -il possible de ramener les termes de ces suites sous la forme
Re: suites-parité
rassan a écrit:bonjour pour un texte plus lisible!
comme je l'ai déjà dit au début , la question de parité est venue au cours
de l'étude d'une suite que j'ai proposé et que je l'appellerai par la suite
suite de digischool1(dS1)qui est :+"Somme des nombres impairs
;pour n entier naturel
En effet les termes de cette suite sont impairs (et qu'il fallait démontrer) et en supposons ainsi ,
qui est la formule que j'ai donné au début.
une autre suite de même nature
(dS2)"somme des nombres pairs
"
pour celle ci il est facile de montrer que
et que tous ces termes(
) se terminent par 1
alors une autre question que je propose :
Est -il possible de ramener les termes de ces suites sous la forme?
Re: suites-parité
On peuT poser
Re: suites-parité
J'ai des doutes concernant l'expression  en fonction de
en fonction de  , car il faut distinguer les cas
, car il faut distinguer les cas  paire ou impair.
paire ou impair.
Re: suites-parité
Razes a écrit:J'ai des doutes concernant l'expressionen fonction de
, car il faut distinguer les cas
paire ou impair.
Bonjour,
De mémoire, l'expression de la 1ère suite est bonne :
Re: suites-parité
Razes a écrit:
On peuT poseret chercher
et
afin que
mais ceci n'a pas de solution, le seule format possible est
Bonjour
plutôt
mais cette forme 'pseudo linéaire est peu encourageante .
en fait les suites
dans notre cas
Re: suites-parité
Bonjour
on peut montrer que pour
pour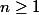
peut -on(savoir) conjecturer le nombre de termes impairs entre ?
?
on peut montrer que
peut -on(savoir) conjecturer le nombre de termes impairs entre
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

