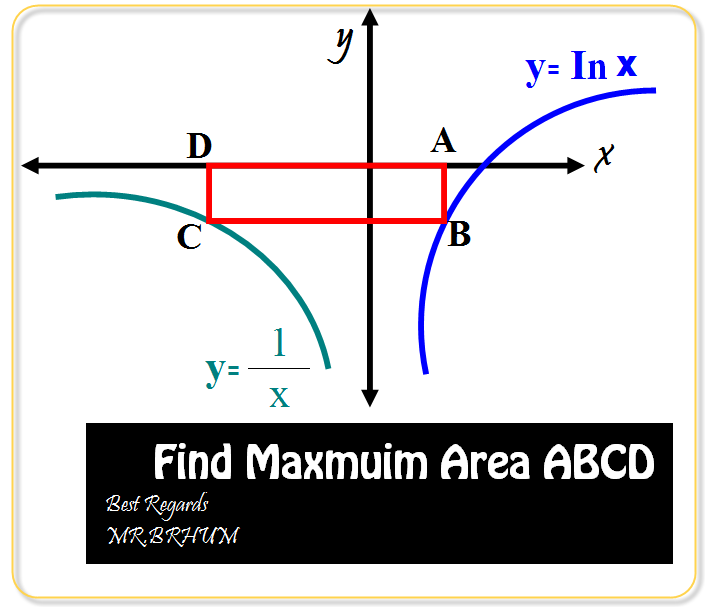
Question
5 messages
- Page 1 sur 1
par Ben314 » 09 Juin 2014, 00:12
Salut,
en supposant que la fin de la phrase est "... is the incircle of triangle (BPC)"
Soit)
un point de l'axe des 
distinct de )
.
La droite
est tangente au cercle de centre )
et de rayon 
lorsque
=1\ \Leftrightarrow\ \frac{|0-a\times 1-b|}{\sqrt{a^2+1}}=1\ \Leftrightarrow\ (a+b)^2=a^2+1\ \Leftrightarrow\ a=\frac{1-b^2}{2b}\ })
De même pour un second point)
de l'axe des avec 
pour que )
soit sur le segment 
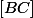de façon à ce que le cercle )
soit un cercle inscrit de )
et pas un cercle exinscrit.
\in\Delta_b\cap\Delta_c\ \Leftrightarrow\ <br />\left\{\matrix{y=\frac{1-b^2}{2b}x+b\cr y=\frac{1-c^2}{2c}x+c \right.\ \Leftrightarrow\ <br />\left\{\matrix{x=\frac{2bc(c-b)}{(1-b^2)c-(1-c^2)b}=\frac{2bc}{1+bc}\cr<br /> y=\frac{1-c^2}{2c}\times\frac{2bc}{1+bc}+c=\frac{b+c}{1+bc}\ \right.)
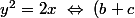^2=4bc(1+bc)\ \Leftrightarrow\ (b-c)^2=4b^2c^2\ \Leftrightarrow\ b-c=2bc)
en supposant que la fin de la phrase est "... is the incircle of triangle (BPC)"
Soit
La droite
De même pour un second point
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 09 Juin 2014, 01:09
Salut,
en supposant que la fin de la phrase est "... is the incircle of triangle (BPC)"
Soit un point de l'axe des distinct de .
La droite est tangente au cercle de centre et de rayon lorsque
=1\ \Leftrightarrow\ \frac{|0-a\times 1-b|}{\sqrt{a^2+1}}=1\ \Leftrightarrow\ (a+b)^2=a^2+1\ \Leftrightarrow\ a=\frac{1-b^2}{2b})
De même pour un second point de l'axe des avec 
-2t^2>0\ \Leftrightarrow\ t>2)
pour )
en supposant que la fin de la phrase est "... is the incircle of triangle (BPC)"
Soit
La droite
De même pour un second point
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :