Démonstration par l'absurde : mon avis... et le vôtre ?

par **ThSQ** » 06 Juil 2008, 14:56

leon1789 a écrit:Que pensez-vous de cette preuve ?

Elle est parfaite.

Qui a dit que les preuves par l'absurde étaient forcément meilleures ?

Ca dépend des cas. Il y a des preuves directes et des preuves par l'absurde (Euclide le 1er) de l'infinitude des nombres premiers. Toutes sont intéressantes je trouve et apportent un éclairage particulier sur le sujet. Dire que seules celles directes sont dignes d'intérêt me parait .... absurde.

par **leon1789** » 06 Juil 2008, 14:57

ThSQ a écrit:Faudrait savoir

mêêêêêêêêêêêêêêêêê !
C'est ce que j'essaie d'expliquer (entre autres) :cry:

Si on a un résultat du type > alors une question naturelle est de savoir comment calculer machin.

Si le résultat > est prouvé de manière "directe", on a le moyen explicite (théorique) de calculer machin : il n'y a rien à faire de plus.

Si le résultat > est prouvé "par l'absurde", alors on n'a aucun moyen de calculer machin en l'état actuel des choses. Mais en travaillant un peu (ou bcp, ça dépend), on peut essayer, quand c'est possible, de trouver une preuve directe dans la preuve par l'absurde. Et une fois cet effort réalisé, c'est gagné... :we:

par **abcd22** » 06 Juil 2008, 15:28

leon1789 a écrit:Si le résultat > est prouvé de manière "directe", on a le moyen explicite (théorique) de calculer machin : il n'y a rien à faire de plus.

Un moyen théorique n'est pas forcément beaucoup plus utile que pas de moyen du tout, par exemple si je dis que le PGCD de deux nombres a et b existe car Z est un anneau principal et qu'on prend un générateur de aZ + bZ, ça ne sert pas à grand chose pour trouver ce PGCD, en pratique j'utiliserai l'algorithme d'Euclide.
Pour reprendre l'exemple des nombres premiers congrus à 3 modulo 4 d'au-dessus, l'algorithme de recherche de tels nombres donné par la démonstration est complètement inutilisable en pratique (il faut faire des factorisations, ce qui est un problème difficile, et en plus avec le produit on arrive vite à des nombres très grands), si je veux vraiment trouver des nombres premiers congrus à 3 modulo 4 j'aurai plus vite fait de tester la primalité de tous les nombres congrus à 3 modulo 4 successivement, donc on ne peut pas vraiment dire que la présence de cet algorithme dans la démonstration soit un plus par rapport à une autre démonstration d'où il serait absent.

par **leon1789** » 06 Juil 2008, 15:35

ThSQ a écrit:Elle est parfaite.
Qui a dit que les preuves par l'absurde étaient forcément meilleures ?

Elle est parfaite, merci :zen: Il me semble qu'on ne la trouve nulle part !!! Et pourtant, elle est simple.

Cela paraît un peu présomptueux de ma part, mais toutes les preuves que j'ai vues (sur le net ou dans les bouquins) de ce lemme sont faites par récurrence et/ou par l'absurde (en partie ou totalement...), voire pire. Bien sûr, dans ces autres preuves, il y a souvent une ébauche de la construction de l'élément séparateur, mais il est noyé dans tout le binz... c'est dommage !

ThSQ a écrit:Ca dépend des cas. Il y a des preuves directes et des preuves par l'absurde (Euclide le 1er) de l'infinitude des nombres premiers. Toutes sont intéressantes je trouve et apportent un éclairage particulier sur le sujet. Dire que seules celles directes sont dignes d'intérêt me parait .... absurde.

Je n'ai pas dit qu'une preuve par l'absurde est sans intérêt. Mais elle laisse comme une espèce de travail inachevé. Une preuve directe est l'occasion d'aller peut-être plus au fond des choses. Pour moi, c'est assez important.

Mais quelle version entre (1) et (2) prendriez-vous pour faire un cours, ou un exposé, ... ?

par **leon1789** » 06 Juil 2008, 15:42

abcd22 a écrit:Un moyen théorique n'est pas forcément beaucoup plus utile que pas de moyen du tout (...) on ne peut pas vraiment dire que la présence de cet algorithme dans la démonstration soit un plus par rapport à une autre démonstration d'où il serait absent.

Je suis d'accord. C'est pour ça que j'écris "algo (théorique)", ce qui est clairement moins bon qu'un "algo (efficace)", mais pas pire qu'un "sans algo !".

Obtenir des méthodes efficaces de calcul, c'est aussi un sport ! (auquel je ne joue pas). Et il est clair que ce n'est pas une collection de preuves par l'absurde qui vont apporter un algorithme tout cuit. :we:

par **leon1789** » 11 Juil 2008, 09:44

leon1789 a écrit:On peut démontrer par récurrence que toute partie non vide de N contient un plus petit élément, l'assertion à démontrer est
H(n) = >

Dans cette discussion http://www.maths-forum.com/showthread.php?t=66162 , Babe donne gentiment cette adresse http://pagesperso-orange.fr/lavau/mpsi2003/mpsi2003.htm entre autres.

A partir de l'axiomatique de Péano, l'auteur présente une preuve (par l'absurde) que toute partie non vide de N admet un plus petit élément. La voici (récurrence dans un raisonnement par l'absurde) :

Démonstration :
Par l'absurde.
Soit A une partie non vide n'admettant pas de plus petit élément. On a :
si n vérifie : alors n minore A, mais comme A ne possède pas de plus petit élément, n ne peut être élément de A. Donc : et prouvons H(n+1) : soit E une partie contenant n+1. Si elle contient un élément , alors H(n) s'applique à E et prouve que E a un plus petit élément. Sinon n+1 est le plus petit élément de E ! Ainsi H(n+1) est prouvé dans tous les cas.

H(n) étant vraie pour tout , on conclut que toute partie non vide (contenant un entier n) possède un plus petit élément.

Je pense que ma démo est beaucoup plus simple et naturelle car elle reflète une manière (naïve) de chercher un plus petit élément dans un ensemble non vide donné explicitement.

Sur cet exemple, quel est l'intérêt du raisonnement par l'absurde ?

par **leon1789** » 11 Juil 2008, 10:08

Et comme parfois (plus souvent que l'on croit), on peut effacer les parties > > de la preuve pour trouver une preuve "directe".

[quote]
Par l'absurde.
Soit A une partie non vide n'admettant pas de plus petit élément. On a :

si n vérifie :

alors n minore A, mais comme A ne possède pas de plus petit élément, n ne peut être élément de A. Donc : [TEX]\forall\ a \in A, n B où A="E est une partie de N n'ayant pas de plus petit élément" et B="E est vide".

Pour moi, on est dans un cas où le raisonnement par l'absurde prouvant "A => B" est du type .... => B. Absurde car non B. Conclusion B vrai[/B] >>. Mais cette démo contient deux preuves de A => B !!

Question pédagogique : dans un cours, quelle proposition doit-on écrire
> ou
> ?
A votre avis ?
(pour moi, c'est la première car je crois qu'elle sert davantage dans ce sens là)

par **leon1789** » 06 Aoû 2008, 11:49

Petite lecture de vacances : > publication de IREM Poitiers en 2000.

J'ai sélectionné quelques passages typiques de problèmes (d'ordre pédagogiques ou techniques) que peut soulever le raisonnement par l'absurde.

Remarquer que les quelques preuves directes que je donne dans la foulée sont simplement extraites des preuves par l'absurde.

Espoir : illustrer encore une fois des abus classiques de l'utilisation de preuves par l'absurde (ici en arithmétique élémentaire) et montrer qu'il y a encore des analyses à tenter après une preuve par l'absurde réalisée au brouillon, analyses permettant à l'occasion (plus souvent que l'on croit) d'alléger les preuves et/ou de dégager de meilleurs outils et/ou de prouver des résultats plus forts...

Résumé en ce qui concerne les raisonnements par l'absurde trouvés dans le document :
- un premier exemple est une preuve par l'absurde qui n'amène à aucune contradiction
(comme une démo de l'hérédité d'une preuve par récurrence sans utiliser l'hypothèse de récurrence) ;
- un autre exemple est une preuve par l'absurde qui prouve beaucoup moins
que la démonstration directe qu'elle contient ;
- un dernier exemple est un raisonnement qui aboutit à une contradiction (tant désirée !), mais pas à cause de l'hypothèse du raisonnement par l'absurde...
- etc.
La brochure a été écrite par 14 co-auteurs (quand même !) : enseignants du secondaire et du supérieur.

--1-- page 21 : preuve de l'unicité du couple "quotient et reste" de la division euclidienne de

par

.

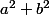
On raisonne par l'absurde. avec soit [TEX]a,b"/> deux entiers premiers entre eux, alors il en est de même pour et .
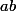
(L'implication réciproque est évidente, il y a donc équivalence.)

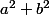
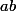
On raisonne par l'absurde, si et ne sont pas premiers entre eux, leur pgcd admet un diviseur premier .
Alors divise donc divise ou divise . Si divise alors il divise , et donc il divise . Alors est un diviseur commun à et , ce qui est exclu. De même le cas divise est exclu. D'où la contradiction.

Voici le cas typique où une preuve directe est "déguisée" en une preuve par l'absurde et dont le résultat final est de prouver une propriété moindre !
En effet, de la preuve par l'absurde, on peut extraire tout simplement la preuve directe de la proposition suivante, plus générale, sans aucune hypothèse sur les entiers et :

l'ensemble E' des diviseurs premiers communs à 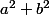et 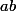est inclus dans l'ensemble E des diviseurs premiers commun à et .
(L'inclusion inverse est évident, on a en fait l'égalité.)

Soit . Alors divise donc divise ou divise .
Si divise alors il divise , et donc il divise . Alors .
De même le cas divise amène à une conclusion identique.

Alors la proprosition --2-- en est simplement le cas particulier où est seulement vide !

Remarque pour aller un poil plus loin :
en fait, symboliquement, la seconde proposition s'écrit

Mais plus précis encore est de montrer (tout aussi facilement que la preuve directe ci-dessus) la formule anodine

impliquant pourtant très rapidement les deux propositions précédentes !

Et enfin, on remarque que cete dernière suite d'inclusions est valide pour
tous éléments d'un anneau commutatif quelconque, sans histoire de premiers...

--3-- page 24, une remarque qui me semble très intéressante :

(...) y a-t-il une démonstration meilleure que les autres ?
Par exemple quelles contraintes impose une démonstration par l'absurde
(au moins connaitre le résultat à démontrer) ?
Est-ce que la véracité d'un résultat est renforcée s'il a été
démontré de plusieurs manières ?
Est-ce qu'une démonstration sert uniquement
à justifier un résultat, ou bien a-t-elle un intérêt en elle-même ?
Un élève qui poursuit des études scientifiques est confronté à des multitudes
démonstrations. Il pense bien souvent que l'enseignant ne les faits que par
plaisir, n'en voit pas l'intérêt. Or il faut qu'il comprenne qu'en mathématiques,
ce sont les démonstrations qui ont une valeur de formation.

--4-- page 48 : après l'exemple --1-- qui met la puce à l'oreille,
voici un exemple où la preuve donnée est fausse,
et le fait qu'elle soit par l'absurde n'arrange rien je crois...

Pour tout entier 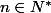, on pose , l'ensemble des multiples stricts de .

Soit un entier 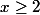non premier ;
l'entier tel que soit le premier ensemble contenant , est premier.

Démonstration : supposons non premier, alors il existe tel que , d'où avec . On en déduit que , avec , ce qui contredit la définition de ; donc est premier.

Je ne sais pas combien de personnes ont relu cette preuve, mais pour moi, cette preuve est fausse :
au moins parce que la proposition à prouver est fausse,
mais plus précisément parce qu'un entier non premier peut être égal à 1.
C'est pourquoi le passage "donc il existe tel que qui est éronné...
et non pas l'hypothèse "supposons q non premier" !
Ce n'est donc pas l'hypothèse initiale du raisonnement qui mène à la contradiction, mais la faute de déduction.

D'ailleurs, il est clair que le premier ensemble contenant parmi les est .
Je m'en suis aperçu (ce n'est pas un exploit, ok ) en voulant travailler cette preuve (pour la rendre "directe"...)

Le problème est de détecter une erreur dans une preuve. Ce n'est pas évident, nous faisons tous des erreurs de raisonnement. Mais il faut dire qu'un raisonnement par l'absurde n'arrange rien à l'affaire, car lors d'une preuve par l'absurde, on est content de tomber sur une contradiction ! (alors qu'une contradiction dans une preuve directe indique évidemment une erreur). On pourrait dire que la nature du raisonnement par l'absurde supprime le garde-fou de la non-contradiction.

Voici maintenant une version correcte et une preuve directe, inspirée bien sûr par la preuve par l'absurde initiale :

Pour tout entier 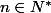, on pose , l'ensemble des multiples stricts de .

Soit un entier 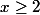non premier ;
l'entier tel que soit le premier ensemble (d'indice 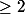) contenant , est premier.

Soit un diviseur strict de . On a , d'où avec .
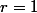
On en déduit que avec , ce qui, d'après la définition de , force ; ainsi , et donc est premier.

par **leon1789** » 09 Aoû 2008, 18:44

Un document qui m'a surpris http://www.irem.uhp-nancy.fr/Lomb/absurde.pdf
L'auteur explique, selon lui, les vrais et faux raisonnements par l'absurde, les raisonnements directs et par contraposition, et prend l'exemple de l'irrationalité de

... Son exposé est proche de certaines choses qui ont été abordées dans cette discussion. Amusant.

par **leon1789** » 21 Aoû 2008, 20:24

Ici http://maths-forum.com/showpost.php?p=426010&postcount=21 , encore une petite preuve qui montre qu'un raisonnement par l'absurde n'est nullement nécessaire pour démontrer l'irrationalité de

. Ce serait ici plutôt par simple contraposition de

.

par **Clembou** » 21 Aoû 2008, 20:26

leon1789 a écrit:Ici http://maths-forum.com/showpost.php?p=426010&postcount=21 , encore une petite preuve très simple qui montre qu'un raisonnement par l'absurde n'est nullement nécessaire pour démontrer que l'irrationalité de .

[HS]
Ah ! Leon, content de te retrouver sur le forum ! :++:
[/HS]

par **leon1789** » 13 Oct 2008, 20:22

Autre exemple : http://www.maths-forum.com/showthread.php?t=70611&highlight=absurde

lunameika a écrit:soit u appartenant à X^N une suite. On suppose qu'elle n'a qu'une seule valeur d'adhérence L et que X est compact. Montrer que u est convergente.

(rappel : dans un compact, tout famille infinie possède une valeur d'adhérence)

abcd22 conseille un raisonnement par l'absurde (contenant une récurrence). Personnellement, je préfère celui-ci, plus rapide car (?) moins "absurde" :

Pour tout , l'ensemble des éléments de extérieurs à la boule ouverte centrée en L et de rayon est fini car n'a pas de valeur d'adhérence dans le compact .
Donc il existe N tel que , .
Et la définition de la convergence de vers L est prouvée.

Vous me direz qu'il y a une petite contraposée à l'intérieure. Certes, mais au moins, les trois petites phrases écrites dans cette preuve sont compatibles avec l'hypothèse.

par **leon1789** » 17 Oct 2008, 20:28

Bon, ça tourne un peu au déballage d'exemples, mais il y en a tant...

Je viens de tomber sur une preuve de P.Samuel (Théorie algébrique des nombres). C'est une preuve par l'absurde qui fait plus d'une demi-page. C'est écrit petit, et la preuve est assez longue en fait.

Comme toutes les preuves par l'absurde, on passe dans un système contradictoire... jusqu'à la manifestation objective d'une contradiction, ce qui termine la preuve.

Personnellement, je pense que plus une preuve par l'absurde est longue, plus il y a des choses à gratter. En lisant cette preuve, on peut facilement extraire deux petits lemmes d'algèbre commutative (posant même des questions plus ouvertes). Et bien sûr, une fois ces lemmes exhibés, la preuve du théorème est soulagée d'autant et un peu plus explicite...

Je me demande quel est le plaisir de gâcher (c'est le mot qu'il convient !) des petits lemmes en les plaçant dans une preuve par l'absurde qui empêche toute récupération ! :hum:

par **Imod** » 17 Oct 2008, 20:31

Humour :we:

Ce fil vire à l'absurde !

Imod

par **leon1789** » 17 Oct 2008, 20:35

Imod a écrit:Humour :we:
Ce fil vire à l'absurde !
Imod

:ptdr: oui, ThSQ l'a déjà fait deux fois (je crois) cette "blague".

Mais bon, que veux-tu... quand on lit ce qu'on lit, on a raison de penser ce qu'on pense :zen: franchement, non ? bon ok :triste:

par **francis21** » 17 Oct 2008, 21:37

oui on a raison de penser ce qu'on pense.

par **leon1789** » 01 Nov 2008, 22:49

Contrairement au théâtre, en math, un raisonnement par l'absurde n'a rien de comique.

Sa complexité se situe entre un raisonnement simplement déductif et un raisonnement par récurrence : j'ai conscience que ceci est totalement subjectif... Mais tout de même, dans les faits, aux écoles, collèges, lycées, on apprend assez tôt le raisonnement hypothético-déductif (mêlé parfois d'une petite contraposée, si si...), puis les raisonnements par l'absurde (à l'occasion !) et enfin celui par récurrence.

Objectivement, il y a cependant plusieurs points communs entre raisonnements par l'absurde et par récurrence :
-- ces deux raisonnements apportent une hypothèse supplémentaire à l'énoncé initial (il me semble que c'est leur intérêt principal !) : dans l'hérédité pour la récurrence, ou par définition dans pour une preuve par l'absurde.
-- mais ces deux raisonnements ont besoin de "connaître" la conclusion qu'ils "veulent" démontrer. C'est une limitation claire.

Enfin, la nature même du raisonnement par l'absurde est de créer un système contradictoire. Par conséquent, a priori, on ne peut rien obtenir d'une preuve par l'absurde si ce n'est la preuve que le système créé est contradictoire. Si (malheureusement !) cela convient à la plupart des matheux, il convient de constater ici encore une limitation de ce raisonnement. En effet, des raisonnements déductifs habituels peuvent amener des résultats intermédiaires ayant leurs intérêts propres (i.e. réutilisables par ailleurs), sans parler de l'aspect constructif des preuves. Dans un raisonnement par l'absurde, tout ceci est évidemment hors propos.

par **ffpower** » 08 Nov 2008, 02:30

un trip que j ai eu hier:supposons qu on a un ensemble A,et qu on montre disons

et on en déduit

A t on fait un raisonnement par l absurde?car ca y ressemble beaucoup mais cela dit la prop

n est pas une prop absurde.Elle dit juste que A est vide.Voila,qu en pensez vous?(ou plutot "qu en penses tu?" XD)

par **jeancam** » 08 Nov 2008, 11:32

la demonstration par l absurde est un lieu privilegié du donc tandis que dans le sens direct c est plutot le car (celui qui fait du direct donc est censé atteidre sa cible, ce qui est plus dure que lorsque que la cible est n importe quelle contradiction)
c est donc pour un débutant comme moi un outil pratique et assez beau...
puisqu on dit des choses vraies(implications) à propos de choses(hypotheses) fausses.

mais la dem par l absurde a pour le débutant une facheuse tendance à lui faire croire qu il a montré quelque chose alors qu il s est juste trompé...

par **leon1789** » 08 Nov 2008, 18:09

ffpower a écrit:un trip que j ai eu hier:supposons qu on a un ensemble A,et qu on montre disons

et on en déduit
A t on fait un raisonnement par l absurde?car ca y ressemble beaucoup mais cela dit la prop n est pas une prop absurde.Elle dit juste que A est vide.Voila,qu en pensez vous?(ou plutot "qu en penses tu?" XD)

Oula, c'est de la logique... et je ne suis pas logicien :triste:

Quelle est la définition "positive" de l'ensemble vide ? Dire que c'est l'ensemble qui ne contient aucun élément, est une définition "négative". Une définition "positive" est peut-être justement la phrase que tu donnes !

=> faux
Mais il faudrait poser la question à un logicien.

Démonstration par l'absurde : mon avis... et le vôtre ?

bonjour

Qui est en ligne