Démonstration par l'absurde : mon avis... et le vôtre ?

ffpower a écrit:Je suis pas sur,mais je crois que c est pas possible de montrer sans "absurde" qu un métrique "séquentiellement" compact est compact au sens de borel lebesgue..

Oui, je veux bien le croire... Tout ça est bien au-delà de mes connaissances en analyse.

En fait, je voudrais préciser un peu les choses car j'ai peut-être exagéré ma pensée (car pas assez nette et évoluante). Dailleurs, il n'y a pas que moi qui exagère :we:

bruce.ml a écrit:(...)Et il ne faut pas oublier que les mathématiques ce n'est pas de l'informatique, on n'a pas besoin d'avoir de preuves constructives !

... bref...


Lorsqu'on a une preuve par l'absurde de A => B, je crois qu'il est bon de refaire une passe de ce genre :

-1- dégager tout ce que A implique raisonnablement, sans utiliser non B. Si on arrive à B, alors on a une preuve directe .

-2- si B n'est pas prouvé alors, dégager ce que non B implique, sans utiliser A !! Si on arrive à non A, alors on a une preuve directe de la contraposée .

Souvent (comme je disais précédemment), ces deux étapes suffisent... Mais pas toujours, et effectivement, il ne faut peut-être pas forcer les choses...

-3- si non A n'est pas prouvé à partir de non B, alors voir si A et non B impliquent des assertions contradictoires : . On obtient ainsi en direct et par contraposée. Là, je dirais qu'on a une preuve non pas par l'absurde, mais "à moitié directe, à moitié par contraposée". Je pense qu'il est important de bien marquer clairement la séparation entre et !

A mon avis, beaucoup de preuves dîtes par l'absurde cache en réalité une telle décomposition en deux temps : c'est bien dommage ! Ici, contrairement à un raisonnement par l'absurde quelconque, certaines assertions sont vraies si A est supposée, et les autres sont vraies si non B est supposée. Donc les assertions sont "réutilisables".

-4- si A => B n'est toujours pas prouvé, alors on doit absolument mixer les conséquences de A et de non B pour arriver à l'absurde : c'est une "vraie preuve par l'absurde".

Ici, contrairement à un raisonnement "moitié direct, moitié contraposée", sous l'hypothèse >, les assertions ne sont prouvées ni vraies ni fausses puisqu'elles impliquent seulement le faux sous l'hypothèse >. Donc leur réutilisation est impossible.


Procéder comme cela ne peut apporter que plus de clarté sur la preuve. Ce n'est pourtant pas ce que l'on voit dans les livres : je ne parle pas des étudiants qui composent en temps limité (peut-on faire de bonnes maths en temps restreint ?...), mais des auteurs qui ont tout le temps de réfléchir à leurs preuves, ou d'autres matheux soucieux de dénicher des petits trucs...

Qu'en pensez-vous ?

Deux petites pensée pour montrer qu'une démonstration par l'absurde n'est pas toujours réductible à une démonstration directe :

• Léon a dit qu'une preuve directe démontre parfois un résultat plus général. Cela montre bien que la preuve directe est plus difficile que la preuve par l'absurde, puisqu'il est rare que l'on puisse montrer réellement plus sans effort supplémentaire.
• La logique intuitionniste rejete le tiers exclu, et donc le raisonnement par l'absurde. Ce n'est pas sans conséquences...

Cependant, je pense comme vous qu'une démonstration par l'absurde n'est pas toujours ce qu'il y a de plus élégant. Et je pense que Léon a mis le doigt sur le critère.
Une démonstration par l'absurde consiste à montrer et et déduire . (Il me semble bien que c'est le cas le plus général, contrairement à ce que dit Léon.)
Quels sont les cas réductibles à une preuve directe ?
Si on peut démontrer la contraposée (logiquement équivalent, mais pas moralement) de l'une des implications, on a une preuve directe.
Si l'une des implication est une équivalence, on a aussi une preuve directe, mais cette fois-ci avec ajout de contenu !
Quelqu'un de motivé pourrais décortiquer les exemples donner dans le fil et déterminé si l'on est passé à une preuve directe par l'une ou l'autre voie.

Dernière remarque : il ne faut pas que la logique formelle fasse oublier les difficultés de rédaction. Pour montrer que , même si l'on a une preuve directe, on ne montre pas l'implication telle quel. On commence par supposer A, puis on travail avec l'ensemble des axiomes plus A. Montrer et , rédactionnellement c'est lourd. On pourrait commencer avec supposer A, montrer C , puis ne plus supposer A, poser et montrer , mais c'est encore trop lourd. Pour une rédaction légère, il est naturel de supposer et de montrer .
Le problème est que n'est pas équivalent à

Lierre Aeripz a écrit:Léon a dit qu'une preuve directe démontre parfois un résultat plus général. Cela montre bien que la preuve directe est plus difficile que la preuve par l'absurde, puisqu'il est rare que l'on puisse montrer réellement plus sans effort supplémentaire.

Je suis d'accord : pour un résultat plus fort, il faut travailler davantage, le contraire serait immoral. Mais cela peut justement être source de motivation.

Le problème est de savoir si on veut faire des preuves les plus expéditives possibles, ou démontrer des résultats de manière la plus précise possible... (l'un étant souvent compatible avec l'autre en fait.)

Lierre Aeripz a écrit:Une démonstration par l'absurde consiste à montrer et et déduire . (Il me semble bien que c'est le cas le plus général, contrairement à ce que dit Léon.)

Je me suis mal exprimé : oui, c'est effectivement le cas le plus fréquent.

Mais pour moi, une démonstration qui a toutes les chances d'être une vraie preuve par l'absurde, c'est une preuve qui associe les hypothèses A et non B pour en déduire une contradiction après plusieurs étapes :
par exemple, A implique qu'un certain ensemble est non vide et non B permet d'en prendre le plus petit élément... puis la preuve se poursuit jusqu'à la contradiction désirée.

Dans cet exemple, rien ne laisse présager que l'on puisse décomposer la preuve en deux parties et car dès le début les hypothèses A et non B sont utilisées. Mais si c'est possible (sans tout dénaturer), alors mon avis est qu'on se doit de le faire pour davantage de clarté.

Lierre Aeripz a écrit:Quels sont les cas réductibles à une preuve directe ?
Si on peut démontrer la contraposée (logiquement équivalent, mais pas moralement) de l'une des implications, on a une preuve directe.

100% d'accord, et là, c'est super ! :zen:

Lierre Aeripz a écrit:Si l'une des implication est une équivalence, on a aussi une preuve directe, mais cette fois-ci avec ajout de contenu !

oui

Lierre Aeripz a écrit:Montrer et , rédactionnellement c'est lourd.

Là, je ne suis pas d'accord : je trouve au contraire que c'est structurant.

Lierre Aeripz a écrit:Pour une rédaction légère, il est naturel de supposer et de montrer .

Si le gain dans la rédaction est faible, je trouve (mais c'est une affaire de goût peut-être) que cela n'en vaut pas la chandelle au niveau de la compréhension.

Lierre Aeripz a écrit:Le problème est que
n'est pas équivalent à

Oui, exactement !
...surtout si on peut prendre C=B , ou même C=A :we:

Lierre Aeripz a écrit:Si on peut démontrer la contraposée (logiquement équivalent, mais pas moralement) de l'une des implications, on a une preuve directe.

Pour montrer que , on raisonne par l'absurde non?

Non..par définition,A=>B c est Non A ou B,donc Non B=>Non A c est Non B ou Non Non A donc equivalant a Non B ou A...

Je dis la chose suivante :
supposons et . Si A, alors B, or , impossible. donc .

yos a écrit:Pour montrer que , on raisonne par l'absurde non?

yos a écrit:Je dis la chose suivante :
supposons et . Si A, alors B, or , impossible. donc .

On peut présenter ça différemment, en preuve directe

Comme le dit ffpower, la définition logique de est " ou ". ok.
Maintenant, si alors ! Voilà.

Dans le même genre :
démontrer que l'inverse d'une application croissante bijective est également (strictement) croissante.

Réponse en preuve "directe" :

Considérons , puis leurs antécédents respectifs par .
Ecrivons l'hypothèse croissante :
puis sa contraposée (+ totalement ordonné) :
d'où strictement croissante. cqfd :happy2:

Dans Arnaudiès-Fraysse , Cours de mathématiques-1 , algèbre

EXEMPLE 1

page 69

Arnaudies-Fraysse a écrit:Soit un morphisme de groupes. Si le noyau de f est réduit à alors f est injectif. (Réciproque évidente)

Preuve :

Arnaudies-Fraysse a écrit:Si f n'est pas injectif alors deux éléments distincts et de G auraient la même image, donc , d'où , d'où et appartiendrait à Kerf, contrairement à l'hypothèse.

Mon impression :
ils ont dû être distraits par le numéro de la page, parce que la preuve (pourtant simple) est rédigée de manière compliquée ! En plus la phrase
> est ambigüe : deux éléments quelconques ou pas ?


Preuve directe (en effaçant le surplus de mots !) :

Soit de même image. On a , d'où , d'où , d'où , donc . Ainsi f est injective.

EXEMPLE 2

page 140

Arnaudies-Fraysse a écrit:L'ensemble P des nombres premiers est infini.

Preuve :

Arnaudies-Fraysse a écrit:On sait déjà que P est non vide. Si P était fini on pourrait former l'entier ; pour tout , on a , donc p ne divise pas N ; cependant N admet au moins un diviseur premier q car . Or un tel q ne serait pas dans P, d'où une contradiction.

Mon avis :
C'est vraiment dommage de mettre tout ça au conditionnel ! En plus, c'est inutile de commencer par dire que P n'est pas vide : la preuve démontre en particulier que P n'est pas vide... (un produit indexé sur le vide vaut 1)


Preuve directe :

Soit des éléments de P (): on peut former l'entier ; pour tout , on a , donc ne divise pas N ; cependant N admet au moins un diviseur premier q car . Ainsi on obtient un (k+1)-ième premier, d'où l'infinité de P par récurrence.

EXEMPLE 3 (plus long, mais encore meilleur !)

page 377

Arnaudies-Fraysse a écrit:Soit une famille d'éléments d'un K-ev E. Cette famille est libre ssi

Preuve :

Arnaudies-Fraysse a écrit:-- Il est bien évident que si l'on avait , c'est-à-dire avec de à support fini, on en déduirait une relation de dépendance linéaire [...] ce qui rend impossible l'indépendance linéaire des .
-- Réciproquement, supposons (*) satisfaite. Imaginons qu'il existe une famille de non tous nuls et à support fini tels que . A partir d'un , on écrirait et donc , contrairement à (*).

Mon avis :
Alors là, c'est le top ! (comme dit sandrine_guillerme dans http://www.maths-forum.com/showpost.php?p=318211&postcount=10)
Les auteurs font deux preuves par l'absurde pour un résultat banal qui se montre d'un seul trait ! En plus, si on regarde les deux preuves par l'absurde, elles sont de cette nature :
on suppose A vraie, puis non B, on montre que non B implique non A sans utiliser A (!), donc non B est absurde, donc B est vraie !
C'est à croire que les auteurs veulent absolument faire dans l'absurde... et cacher le truc essentiel (mais banal) : tout élément non nul d'un corps est inversible.

Je pense que la preuve montre que l'énoncé est mis à l'envers ! En fait, l'énoncé qui colle à la preuve est celui-ci :

Soit une famille d'éléments d'un K-ev E. Cette famille est liée ssi

Preuve :

La famille est liée
où non tous nuls et à support fini
il existe tel que où est à support fini et
il existe tel que

Ainsi la preuve est en parfaite adéquation avec l'énoncé, et la propriété du livre n'en est que la contraposée tout simplement...

Rien dit désolé.

Ah, j'oubliais un argument qui joue en défaveur du raisonnement par l'absurde, spécialement pour les étudiants : quand on fait un raisonnement par l'absurde, on cherche une contradiction... Or quand on en trouve une, est-on certain que cela provient réellement des hypothèses contradictoires, ou bien d'une simple erreur de raisonnement ? ...et des erreurs, tout le monde en fait !

Sur la page http://www.les-mathematiques.net/b/a/a/node6.php3 , il y a plusieurs démonstrations fausses. En voici un exemple :

Troisième point de la démonstration principale : il s'agit de démontrer que

si tout ensemble non vide d'idéaux d'un anneau commutatif A possède un élément maximal pour l'inclusion alors tout idéal de A est finiment engendré.

Preuve par l'absurde, mais erronée :

Soit un idéal de . Supposons que ne soit pas finiment engendré. Alors il existe tel que est un idéal de contenant mais non contenu dans . n'est pas non plus finiment engendré car si c'était le cas, il en serait de même de (*). On construit de la même façon un idéal où est un élément de tel que ne soit pas contenu dans . Par récurrence on construit une suite d'idéaux de A tel que chaque idéal est inclu strictement dans l'idéal . Mais la suite possède, par hypothèse, un élément maximal et est donc stationnaire. Ceci est en contradiction avec le fait qu'elle soit strictement croissante. L'idéal est donc finiment engendré.

(*) c'est faux : prendre par exemple !
Au lieu de chercher une suite strictement croissante contenant , il faut la chercher dans !

En fait, une preuve directe est sur la même idée que la preuve ci-dessus et démontre la contraposée de l'assertion :

(A) S'il existe un idéal non finiment engendré alors (B) il existe une suite strictement croissante d'idéaux et donc (C) un ensemble infini d'idéaux (inclus dans ) sans élément maximal pour l'inclusion.

Preuve directe et très naturelle :

Soit un idéal non finiment engendré.
Admettons connaitre un idéal finiment engendré, inclus dans (on peut prendre par exemple).
On a forcément , donc il existe un élément . On considère alors l'idéal : c'est un idéal finiment engendré, inclus dans , et contenant strictement .
Le procédé se répètant une infinité de fois (axiome du choix...), on constate qu'il existe une suite strictement croissante d'idéaux : ces idéaux forment un ensemble infini sans plus grand élément.

Et la "réciproque", qui la fait ? :we:

-- (non A) Si tout idéal est finiment engendré alors (non B) toute suite croissante d'idéaux est stationnaire.
-- (C) S'il existe un ensemble non vide d'idéaux sans élément maximal pour l'inclusion alors (B) il existe une suite strictement croissante d'idéaux.

Finalement, on a (A) => (B) , (non A) => (non B) , et (B) (C)


Question :
(B) et (C) sont bien équivalentes. Qu'en est-il réellement de (A) et (B) ?
En effet, puisqu'on part de (A) pour arriver à (B) et de (non A) pour arriver à (non B), est-ce que notion d'idéal (in-)finiment engendré ne serait-elle pas moralement plus "avancée" que la notion de suite (strictement) croissante ?!

Bloud a écrit:Rien dit désolé.

ben, faut pas rester comme ça... :help: :we:

J'ai pas tout lu mais je partage la forme de "frustration" associée à une démo par l'absurde. C'est souvent plus satisfaisant d'avoir une preuve directe.

D'ailleurs il y a une école qui essaye d'exclure "le tiers exclu" :

http://fr.wikipedia.org/wiki/Constructivisme_(math%C3%A9matiques)

Tout ça se soigne! Léon qui veut prouver par l'absurde qu'il est mauvais de faire des preuves par l'absurde ... Soyons sérieux : aucun mathématicien (ou auteur de livre de maths) n'écarte ce type de démonstration.

ThSQ a écrit:J'ai pas tout lu mais je partage la forme de "frustration" associée à une démo par l'absurde. C'est souvent plus satisfaisant d'avoir une preuve directe.
D'ailleurs il y a une école qui essaye d'exclure "le tiers exclu" :
http://fr.wikipedia.org/wiki/Constructivisme_(math%C3%A9matiques)

Il y a effectivement les maths constructives, les intuitionnistes, ... Eux, ils sont prêts à nier certains axiomes (tiers exclus principalement) et s'y tenir dur comme fer. En particulier, ils refusent contraposées et les démos par l'absurde.

En ce qui me concerne, c'est seulement un sentiment personnel, et je ne tiens absolument pas à nier le tiers exclus : par exemple, je préfère des énoncés allant dans le même sens que leur démonstration. Ensuite, on peut aussi utiliser les propriétés dans leur sens contraposé.

yos a écrit:Tout ça se soigne!

Mais qui est malade ? ...ceux qui usent et abusent de raisonnements commençant systématiquement par >. Est-ce que faire des preuves mathématiques, c'est adopter un tel esprit de contradiction ?

yos a écrit: Léon qui veut prouver par l'absurde qu'il est mauvais de faire des preuves par l'absurde ... Soyons sérieux : aucun mathématicien (ou auteur de livre de maths) n'écarte ce type de démonstration.

Bon, un petit résumé...

-1- je trouve que certains auteurs en font trop par l'aburde, ce qui alourdit parfois les démos et les rend un poil plus difficiles : exemples avec Arnaudiès (et pourtant Arnaudiès considère le coté algorithmique des maths...)
voir le troisième exemple de http://www.maths-forum.com/showpost.php?p=320267&postcount=30

-2- je pense que faire une preuve par l'absurde réduit parfois le "champ d'action" du raisonnement développé dans cette preuve : voir http://www.maths-forum.com/showthread.php?p=317463#post317463

-3- une preuve par l'absurde de "A => B" est souvent du type "A => C" , et "non B => non C". Pourquoi ne pas le rédiger clairement ? (au lieu de "A et non B => faux"... surtout quand C = A...)

Je ne sais pas si je dis des trucs absurdes. Evidemment que je n'ai pas raison à 100% (..."sinon" on le saurait depuis longtemps !). Mais j'aimerais bien que tu répondes sérieusement à ces remarques.

leon1789 a écrit:En ce qui me concerne, c'est seulement un sentiment personnel, et je ne tiens absolument pas à nier le tiers exclus

Encore heureux. Sans le tiers exclus tu ne peux faire aucune mathématique.

leon1789 a écrit:par exemple, je préfère des énoncés allant dans le même sens que leur démonstration. Ensuite, on peut aussi utiliser les propriétés dans leur sens contraposé.
Mais qui est malade ? ...ceux qui usent et abusent de raisonnements commençant systématiquement par >. Est-ce que faire des preuves mathématiques, c'est adopter un tel esprit de contradiction ?

Mais il faudrait que tu nous dises si c'est pour des raisons religieuses, ou bien pédagogiques.
Si c'est du domaine religieux, je parlerais volontier de maladie, mais je crains qu'il n'y ait pas de remède. Si c'est pour des raisons pédagogiques, on peut faire quelquechose (peut-être). Il y a quelques décennies, on abordait le raisonnement par l'absurde en même temps que les autres démonstrations, notamment en géométrie, et ça passait assez bien. Aujourd'hui on fait ça au lycée et les élèves tirent des gueules jusque par terre (pas les meilleurs) en voyant ce genre de raisonnement. Il est certain que c'est très formateur pour l'esprit de penser ainsi.
Quant à la distinction entre " par contraposée" et "par l'absurde", c'est du domaine du psychologique. Pour moi il n'y en a pas.

La négation est dans la nature : les irrationnels sont définis comment? Comme des réels n'appartenant pas à Q. Et c'est pas pour rien qu'une preuve d'irrationnalité se fait le plus souvent par l'absurde.
Pour prouver que (x+1)/(x-1) ne prend pas la valeur 1, on raisonne par l'absurde (à moins d'être maso et d'étudier la fonction : si c'est ça que tu appelles "une preuve directe en dit plus"...).

leon1789 a écrit:-1- je trouve que certains auteurs en font trop par l'aburde, ce qui alourdit parfois les démos et les rend un poil plus difficiles : exemples avec Arnaudiès

J'ai rien contre les preuves d'Arnaudiès. Celles que tu proposes en remplacement sont parfois lourdes.

leon1789 a écrit:-2- je pense que faire une preuve par l'absurde réduit parfois le "champ d'action" du raisonnement développé dans cette preuve : voir http://www.maths-forum.com/showthread.php?p=317463#post317463

Aucun rapport avec le raisonnement par l'absurde : tu n'as pas simplement donné une preuve directe, tu as changé tout l'exercice. On aurait aussi pu le faire par l'absurde. Les champs d'action sont strictement les mêmes.

yos a écrit:Encore heureux. Sans le tiers exclus tu ne peux faire aucune mathématique.

Heu, là tu exagères un peu... mais, bon, là n'est pas le problème.

yos a écrit:Mais il faudrait que tu nous dises si c'est pour des raisons religieuses, ou bien pédagogiques.

Pédagogiques oui, mais aussi parfois plus personnelles : j'ai l'impression de mieux comprendre avec une preuve qui va dans le même sens que l'énoncé.

Des fois, j'ai eu des idées suite des "retournements" de preuves par l'absurde.

yos a écrit:Il y a quelques décennies, on abordait le raisonnement par l'absurde en même temps que les autres démonstrations, notamment en géométrie, et ça passait assez bien. Aujourd'hui on fait ça au lycée et les élèves tirent des gueules jusque par terre (pas les meilleurs) en voyant ce genre de raisonnement. Il est certain que c'est très formateur pour l'esprit de penser ainsi.

Je suis d'accord que c'est un raisonnement important. D'ailleurs, cela ne me dérange pas du tout de faire un raisonnement par l'absurde dans un premier temps : face à un problème, on essayer au brouillon de trouver un chemin (ça, c'est le plus difficile, et ébaucher un raisonnement par l'absurde peut être efficace) et ensuite on essayer de rendre présentable lors de la rédaction, en dégageant les idées directrices, etc.

yos a écrit:Quant à la distinction entre " par contraposée" et "par l'absurde", c'est du domaine du psychologique. Pour moi il n'y en a pas.

ok, c'est ton avis.

yos a écrit:La négation est dans la nature : les irrationnels sont définis comment? Comme des réels n'appartenant pas à Q. Et c'est pas pour rien qu'une preuve d'irrationnalité se fait le plus souvent par l'absurde.

Pour prouver que (x+1)/(x-1) ne prend pas la valeur 1, on raisonne par l'absurde (à moins d'être maso et d'étudier la fonction : si c'est ça que tu appelles "une preuve directe en dit plus"...).

Lorsque , il me semble que : c'est assez usuel, mais bon, tu peux voir ça comme absurde...

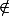
En fait, le problème que tu soulèves ici, dans ces deux exemples, c'est l'utilisation des symboles et dans les preuves par l'absurde, et celle des symboles et dans les preuves "directes". Je ne vois pas d'autres différences ici, et pour moi, ces différences n'ont pas lieu d'être en réalité. Si ?


J'ai lu sur internet qu'un raisonnement par l'absurde était utile pour démontrer que 1 n'est pas solution de X^2+X+1 = 0... Bon là, je trouve que cela complique tout.

D'un autre coté, de si petits exemples (qui se font de tête, dans un sens ou dans un autre) sont un peu stériles. Il faut prendre des exemples plus conséquents...

yos a écrit:J'ai rien contre les preuves d'Arnaudiès. Celles que tu proposes en remplacement sont parfois lourdes.

Cela m'étonne car, pour écrire ces preuves, je n'ai fait qu'extraire certaines lignes des preuves d'Arnaudiès, justement pour montrer qu'il en écrivait de trop dans les exemples 1 et (surtout) 3.

Dans l'exemple 2, au niveau rédaction, la seule différence se situe à la fin des preuves : > ou > . C'est dommage de ne pas voir le coté algorithmique de la démo, et de tout remettre en absurde.

yos a écrit:Aucun rapport avec le raisonnement par l'absurde : tu n'as pas simplement donné une preuve directe, tu as changé tout l'exercice. On aurait aussi pu le faire par l'absurde. Les champs d'action sont strictement les mêmes.

Aucun rapport ? je ne sais pas :

Soit a,b deux entiers premiers entre eux.
Montrer que a+b et ab sont premiers entre eux.

Rain' prend un nombre premier p divisant et ... en supposant que c'est possible (sans le dire d'ailleurs...) !!
Ensuite, grâce à et , il montre que p divise a^2 et b^2, donc a et b (puisque p est premier). Or : absurde... Donc et sont premiers entre eux.

On remarque qu'en fait Rain' a prouvé de manière directe la contraposée du résultat demandé : si a+b et ab ne sont pas étrangers alors a et b ne le sont pas non plus.

Par ailleurs, l'emploi des nombres premiers (ou des polynômes irréductibles) est assez classique, certes, mais là pour ce genre d'exo, c'est absolument inutile.

Personnellement, j'ai pris un nombre quelconque d divisant et : c'est toujours possible, quitte à prendre .
Ensuite, grâce à et (exactement le même argument que Rian' !!!), je dis que d divise . Or .

Ainsi, on arrive à cette assertion réutilisable à volonté :

Quels que soient les entiers a,b, divise

Maintenant entraine de suite ...

J'ajoute même que, et c'est important, c'est en voulant ré-écrire la preuve de Rian' par une démo directe qu'on arrive à énoncer la relation de divisibilité ci-dessus. Cette relation surclasse l'énoncé, et pourtant, elle arrive très naturellement... Bien sûr, la fin de la preuve de Rian' a été modifiée, mais c'est justement ce changement qui apporte un résultat plus fort. Mais, encore une fois, ce changement vient "naturellement" quand on se pose la question : pourquoi utiliser des nombres premiers dans cette preuve par l'absurde de Rian' ?

De plus, libéré de la notion de nombre premier (mais en pensant à la relation de Bézout ), on peut généraliser avec les idéaux

dans un anneau commutatif quelconque... Le champ d'action est ouvert, et cette histoire est sans réel rapport avec les nombres premiers.


Je ne pense pas avoir changé l'exo, mais seulement avoir démontré davantage que la preuve par l'absurde.