Démonstration par l'absurde : mon avis... et le vôtre ?

[ThSQ]

Discussion intéressante mais qui commence à friser .... l'absurde.

[leon1789]

Joyeux Noël :ptdr:

Discussion intéressante mais qui commence à friser .... l'absurde.

C'est un brin d'humour, ou ... :we:
Je trouve aussi la discussion intéressante, mais il ne faut pas que cela tourne au dialogue de sourds bien sûr.

Les arguments généraux de yos sont bons, et il n'a pas tord (je dirais même que je ne suis pas super clair sur "tout" ce que je voudrais dire) : on constate très bien que nous n'avons pas les mêmes idées, les mêmes expériences. Et c'est tant mieux, car c'est ça la beauté de la diversité !

En revanche, je ne comprends pas du tout ses critiques sur mes propositions concernant les exemples d'Arnaudiès et de Rian'... :hein: Si on pouvait m'expliquer avec quelques détails...

[_-Gaara-_]

Joyeux Noël :ptdr:

Oui ! joyeux noël à toi aussi et à tout le monde d'ailleurs y compris le père noël :we: il ne faut pas perdre de vue que se chamailler ne mène à rien. :rulaiz:

c'était mon coté philosophe.. :space:



:salut:


je sors

[leon1789]

il ne faut pas perdre de vue que se chamailler ne mène à rien. :rulaiz:

Ok, mais je ne vois pas où il y a chamaillerie. Je présente mes idées, je demande ce que les gens en pensent, ils me répondent : ils sont d'accord ou pas. Il n'y a pas de problème., le tout est d'argumenter un peu (...comme en maths :we: )

[_-Gaara-_]

Je sais bien ^^ c'est pour cela que j'ai dis qu'il ne fallait pas perdre de vue ce fait. Sinon, je respecte les idées de tout le monde et rien de mieux que d'argumenter. :king2:

Et en lisant le fil, je suis impressionné par tout ce qui a été dit. çà m'a permis d'apprendre des choses. :zen:

[SimonB]

Et en lisant le fil, je suis impressionné par tout ce qui a été dit. çà m'a permis d'apprendre des choses. :zen:

+1. Toutes vos discussions me font repenser ma manière d'envisager les mathématiques, et la didactique, chose fort importante pour moi dans la mesure où je veux passer l'agreg pour devenir prof. Donc, continuez ! (Sans vous envoyer des volées de bois vert, toutefois )

[yos]

...dans la mesure où je veux passer l'agreg pour devenir prof.

Très bonne idée.

Donc, continuez ! (Sans vous envoyer des volées de bois vert, toutefois).

C'est noté.
Dans ce genre de discussion, il y a une part de sectarisme des deux côtés et je ne crois pas à la possibilité pour l'un de convaincre l'autre. Cependant, il y a d'autres lecteurs de la discussion que les deux ou trois "adversaires" et pour eux je crois utile de poursuivre et de ne pas laisser dire si j'ai une opinion contraire.

[leon1789]

Ah encore un tout petit exemple (qui ne sera pas plus convainquant que ça) que je viens de voir passer...

Dans l'anneau des polynômes Z[x], montrer que l'idéal engendré par et 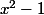est propre, c'est-à-dire qu'il ne contient pas 1.

Preuve par l'absurde : écrivons . Evaluons x en 1 : on obtient . Faux, donc 1 n'est pas dans l'idéal. (...et on s'arrête là.)

Ok, la preuve est rapide et absolument correcte. Mais le fait de la mettre (avec le même argument principal) dans un sens direct permet de conclure davantage :

Preuve directe : soit un entier n dans l'idéal . Ecrivons Evaluons x en 1 : on obtient Donc . En particulier I est propre... mais on peut continuer ! I contient 2, donc on a en fait : on dit que la trace de I sur Z est l'idéal 2Z. Cela pourrait être utile...



Evidemment, cet exemple n'est pas ultra génial. Mais je voulais dire qu'une preuve par l'absurde est "fermée". Le fait d'essayer de la découper et de la retourner si possible donne lieu à une réflexion (ce qui n'est pas mauvais en soi), pour par exemple comprendre les arguments essentiels de la preuve. C'est parfois l'occasion d'apprendre des trucs au passage...

[Alpha]

Je n'ai pas tout lu, mais je tenais à dire que selon moi, les preuves par l'absurde sont souvent plus intuitives que les autres. Souvent, on ne sait pas comment partir, alors on essaie de supposer le contraire, et on voit assez facilement où est la contradiction.
Personnellement, je n'évalue pas vraiment la beauté d'une preuve à sa simplicité, mais plutôt à son caractère intuitif. Une preuve courte et simple, mais qui semble parachutée de nulle part, ne me passionne pas vraiment.
Ce qui ne veut pas dire qu'une preuve par l'absurde est forcément intuitive, ni qu'une preuve directe ne peut pas venir plus rapidement à l'esprit et être plus intuitive qu'une preuve par l'absurde.

[leon1789]

Je n'ai pas tout lu, mais je tenais à dire que selon moi, les preuves par l'absurde sont souvent plus intuitives que les autres. Souvent, on ne sait pas comment partir, alors on essaie de supposer le contraire, et on voit assez facilement où est la contradiction. (...)

Oui, c'est certain, on est d'accord : quand on veut démontrer que A => B, on regarde ce que A implique, ce que "non B" implique, ce qu'on obtient quand on melange tout ça, etc.

D'ailleurs (comme je l'expliquais quelque part au-dessus, mais je comprends parfaitement que tu n'aies pas tout lu...), rédiger une preuve initialement par l'absurde sous la forme "A => C" et "non B => non C" (donc A => B), c'est déjà un premier effort très souvent réalisable facilement...

La question (qui me semble intéressante, mais pas fondamentale certes...) est la suivante : quand on vient d'établir un résultat, est-ce qu'on a terminé sa journée ? Est-ce qu'on plie bagage et hop, on rentre à la maison ? (reviens Léon, j'ai le même (résultat) à la maison ! ...ok ok :we: )

Non, je ne crois pas que les choses s'arrêtent là : on peut encore faire un petit effort pour essayer de gratter quelque chose. On peut parler de rédaction et d'esthétisme, mais là n'est pas mon propos. Trop souvent, on entend qu'une preuve directe est plus "belle" qu'une preuve par l'absurde. Cela est assez discutable : on peut aussi aimer les preuves "intuitives" comme le dit Alpha, ou les preuves "historiques" comme SimonB le disait, etc.

Personnellement, ce n'est pas ça qui me poussent à essayer de ré-écrire les preuves dans un sens direct : c'est parce que je pense qu'on peut de temps en temps y gagner mathématiquement. Cet exercice peut être l'occasion de simplifier la preuve, de se défaire d'argument inutile, d'établir des résultats réutilisables (contrairement à ce qu'on trouve dans une preuve par l'absurde). Mais bien sûr, ça ne marche à tous les coups, sinon ça se saurait :zen:

Par exemple :
http://www.maths-forum.com/showpost.php?p=321738&postcount=40
http://www.maths-forum.com/showpost.php?p=320267&postcount=30
http://www.maths-forum.com/showpost.php?p=339945&postcount=48

Un truc aussi auquel je n'avais pas pensé avant d'en discuter sur le forum : il est "bien" d'énoncer des propriétés qui reflettent leurs preuves. Si la preuve montre que "A et non C => non B", pourquoi énoncer seulement "A et B => C" ? (faut voir sur des exemples...)

[abcd22]

Si la preuve montre que "A et non C => non B", pourquoi énoncer seulement "A et B => C" ? (faut voir sur des exemples...)

Euh ce sont des propositions équivalentes, si j'ai « A et B => C » dans mon cours, le jour où je dois montrer non B et que ce n'est pas trop dur de montrer A et non C je suis censée être capable d'utiliser mon cours pour en déduire non B sans qu'il soit nécessaire d'écrire explicitement cette implication dans le cours, si on commence comme ça on va aussi s'amuser à écrire les contraposées de toutes les propositions qu'on démontre, ça peut être intéressant de réfléchir à ce genre d'équivalences à titre d'exercice mais ça ne vaut pas le coup de tout écrire dans un cours/livre, les élèves sont censés réfléchir un peu par eux-mêmes et savoir comment passer d'une proposition à sa contraposée.

[ThSQ]

Tu ne fais jamais de preuve par récurrence Léon ?

[leon1789]

Tu ne fais jamais de preuve par récurrence Léon ?

Je réfléchissais à ce que j'allais répondre à abcd22... Mais ta question est plus simple :we: donc je réponds : heu, oui j'en fais des fois !
Cela dit, je ne vois pas où tu veux en venir :doh:

[ThSQ]

Le raisonnement par récurrence n'est-il pas le plus bel exemple de reducio ad absurdum ?

[leon1789]

Tu veux dire que ce n'est pas la même chose qu'une preuve "directe" ?
Oui, pourquoi pas, cela pourrait être aussi un sujet de travail : essayer de rédiger de manière directe une preuve donnée par récurrence. Là, c'est certain qu'on apprendrait des choses. Mais ça doit être super dur ! Non ?

[ThSQ]

Tu veux dire que ce n'est pas la même chose qu'une preuve "directe" ?

Heu non, la base du principe de récurrence c'est que si c'était pas vrai pour tout n on pourrait prendre le plus petit n tq .... Si c'est pas un raisonnement par l'absurde ça !

A moins que tu puisses nous donner une autre approche de la récurrence (mais j'en doute) ??

[leon1789]

Merci pour cette remarque thSQ :id:

Pour moi, le principe de récurrence suit exactement la définition (récursive) des entiers naturels (un premier élément et un foncteur >). Ce n'est pas du tout un raisonnement par l'absurde, mais un type de raisonnement "collant à la peau de N".

Heu non, la base du principe de récurrence c'est que si c'était pas vrai pour tout n on pourrait prendre le plus petit n tq .... Si c'est pas un raisonnement par l'absurde ça !

Effectivement, ce début de raisonnement par l'absurde > ou > est très usuel. Je crois qu'il simplifie notablement la rédaction, mais peut-être pas la compréhension (puisque, par essence même, il traite de choses qui n'existent absolument pas !)

Bref, je crois qu'en général ce type de raisonnement cache une méthode de calcul. C'est tout à fait le genre de preuve que j'aime "retourner". (quand j'y arrive...) Ah, il faut que je trouve des exemples pas compliqués de ça ! :we:

[ThSQ]

>> Ce n'est pas du tout un raisonnement par l'absurde

Tu es d'une mauvaise foi assez déconcertante Léon .... :lol2:

Montre-moi/nous la validité générale du raisonnement par récurrence sans utiliser le raisonnement par l'absurde.

Il y a deux ingrédients essentiels : l'existence d'un plus petit élément à toute partie non vide de IN et le raisonnement par l'absurde.

[leon1789]

>> Ce n'est pas du tout un raisonnement par l'absurde

Tu es d'une mauvaise foi assez déconcertante Léon .... :lol2:

Montre-moi/nous la validité générale du raisonnement par récurrence sans utiliser le raisonnement par l'absurde.

Il y a deux ingrédients essentiels : l'existence d'un plus petit élément à toute partie non vide de IN et le raisonnement par l'absurde.

Ton esprit est tourné à l'envers sur ce coup ThSQ ! :ptdr:
En fait, c'est une question d'axiomatique pure et dure... pffff j'aime pas ça !

Définition des entiers naturels :
soit le premier entier 0 = {}, puis le deuxième 1 = {0}, puis le troisième 2 = {0,1}, et puis 3 = {0,1,2}, etc. L'entier successeur d'un entier donné n est l'ensemble des entiers déjà définis {0,1,...n}.

Une preuve par récurrence est une preuve qui valide la propriété pour 0 (initialisation), et qui est "compatible" avec la fonction successeur (hérédité).

On peut démontrer par récurrence que toute partie non vide de N contient un plus petit élément, l'assertion à démontrer est
H(n) = >

On peut aussi aller voir sur http://fr.wikipedia.org/wiki/Raisonnement_par_r%C3%A9currence
où ils disent

Le raisonnement par récurrence est une propriété fondamentale des entiers naturels, et c'est le principal des axiomes de Peano

Ils disent aussi que la récurrence est une manière équivalente de reformuler le bon ordre et que > est la contraposition du bon ordre... Et ils disent encore plein de trucs intéressants sur l'axiomatique...

[abcd22]

> est la contraposition du bon ordre...

C'est la définition de bon ordre ça (la contraposée est correcte dans wikipedia).