Ensemble des entiers naturels
95 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Ensemble des entiers naturels
Bonsoir à tous.
Une question plutôt curieuse: Si on tire au hasard un nombre parmi l'ensemble des entiers naturels, quelle valeur moyenne aura ce nombre ?
Je pressens une réponse, mais elle ne m'inspire pas du tout....
Une question plutôt curieuse: Si on tire au hasard un nombre parmi l'ensemble des entiers naturels, quelle valeur moyenne aura ce nombre ?
Je pressens une réponse, mais elle ne m'inspire pas du tout....
Bonjour,
il faut préciser ce que tu entends par choisir un nombre au hasard, car par exemple si on prend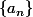 une suite de nombres réels positifs de somme
une suite de nombres réels positifs de somme  et on pose
et on pose 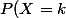=a_k) , où
, où  est une variable aléatoire qui modélise ce choix. Et dans ce cas on obtient des sommes différentes pour l'espérance quand elle est finie.
est une variable aléatoire qui modélise ce choix. Et dans ce cas on obtient des sommes différentes pour l'espérance quand elle est finie.
il faut préciser ce que tu entends par choisir un nombre au hasard, car par exemple si on prend
girdav a écrit:Bonjour,
il faut préciser ce que tu entends par choisir un nombre au hasard, car par exemple si on prendune suite de nombres réels positifs de somme
et on pose
, où
est une variable aléatoire qui modélise ce choix. Et dans ce cas on obtient des sommes différentes pour l'espérance quand elle est finie.
Je donne ici au mot hasard le même sens que lorsque l'on pioche dans un sac un numéro. La particularité de ce sac est qu'il contient tous les entiers naturels et donc ils ont tous la même chance d'être choisis. Autant le 1 que 124572431579865213457698546131424.
nodjim a écrit:Bonsoir à tous.
Une question plutôt curieuse: Si on tire au hasard un nombre parmi l'ensemble des entiers naturels, quelle valeur moyenne aura ce nombre ?
Je pressens une réponse, mais elle ne m'inspire pas du tout....
Il me semble bien que lorsque j'avais essayé de faire cela pour des calculs de probas,
Ben314 m'avait dit que c'était impossible de choisir un entier au hasard (d'équiprobabilité),
et cela ne plaisait pas beaucoup à Doraki non plus dans une discussion où je faisais un peu cela pour additionner la-des probas de 1/...
Donc mon avis que je suis le seul à autoriser, c'est que tout n est "milieu" de n-a, n+a,n-b n+b
donc tout n serait moyenne ce qui revient à dire qu'il n'y aurait pas de moyenne.
sans compter sur le fait que ce que je raconte n'a peut-ètre aucun sens!!!!!!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:Il me semble bien que lorsque j'avais essayé de faire cela pour des calculs de probas,
Ben314 m'avait dit que c'était impossible de choisir un entier au hasard (d'équiprobabilité),
et cela ne plaisait pas beaucoup à Doraki non plus dans une discussion où je faisais un peu cela pour additionner la-des probas de 1/...
Donc mon avis que je suis le seul à autoriser, c'est que tout n est "milieu" de n-a, n+a,n-b n+b
donc tout n serait moyenne ce qui revient à dire qu'il n'y aurait pas de moyenne.
sans compter sur le fait que ce que je raconte n'a peut-ètre aucun sens!!!!!!
Peut on tout au moins tenter d'établir une proba de sortie selon la taille du nombre ?
Par exemple est ce qu'un nombre à 30 chiffres à plus de proba de sortir qu'un nombre à 10 chiffres ?
j'aurais du rester sur c'est pas possible de tirer au hasard un entier,
cela m'aurait éviter de donner une réponse à coté de la plaque dans les entiers relatifs ...
comme tu me l'as déjà dit un jour nodjim,
certaines erreurs naissent de la fausse reconnaissance d'un problème similaire,...
j'avais en tète le zéro des courbes de gain du pile ou face...
cela m'aurait éviter de donner une réponse à coté de la plaque dans les entiers relatifs ...
comme tu me l'as déjà dit un jour nodjim,
certaines erreurs naissent de la fausse reconnaissance d'un problème similaire,...
j'avais en tète le zéro des courbes de gain du pile ou face...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
nodjim a écrit:Peut on tout au moins tenter d'établir une proba de sortie selon la taille du nombre ?
Par exemple est ce qu'un nombre à 30 chiffres à plus de proba de sortir qu'un nombre à 10 chiffres ?
ça devient intéressant,
et j'attends les réponses de nos pointures ...
peut-on multiplier quelque chose qui n'existe pas par deux nombres différents?,
ou bien peut-on ordonner néanmoins de l'incalculable
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Oui, le problème ici est différent. Plus simple peut être mais pas très abordable.
J'avance ceci: Si on fait la somme des nombres compris entre 0 et n très très grand, la valeur est n²/2 et la moyenne donc n/2. Mais comme on a pris l'ensemble N complet, ben le plus grand est à l'infini et donc sa moitié aussi. Alors on tirerait sans doute un nombre à valeur infinie, mais ça n'existe pas, n'est ce pas ?
J'avance ceci: Si on fait la somme des nombres compris entre 0 et n très très grand, la valeur est n²/2 et la moyenne donc n/2. Mais comme on a pris l'ensemble N complet, ben le plus grand est à l'infini et donc sa moitié aussi. Alors on tirerait sans doute un nombre à valeur infinie, mais ça n'existe pas, n'est ce pas ?
Je confirme qu'il n'est pas possible de tirer uniformément un nombre sur N tout entier (ou sur Z, ou sur R...)
Par ailleurs une variable aléatoire peut très bien être définié sans pour autant avoir d'espérance... Exemple : variable aléatoire de Cauchy.
Par ailleurs une variable aléatoire peut très bien être définié sans pour autant avoir d'espérance... Exemple : variable aléatoire de Cauchy.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Bon je donne mon idée, même si elle ne relève d'aucune théorie.
Le nombre qu'on va tirer peut difficilement ne comporter qu'un seul chiffre, ils ne sont que 10 dans ce cas, et par rapport aux nombres à 20 chiffres par exemple, la proba est quasi nulle (10/10^20).
De même, ça peut être difficilement un des nombres à 20 chiffres, ils sont vraiment peu nombreux par rapport aux nombres à 40 chiffres.
Et ainsi de suite.....
La seule issue est que le nombre ait une infinité de chiffres. Tout nombre fini a une chance quasi nulle de sortir par rapport aux nombres illimités, car ils sont infiniment moins nombreux. Mais, je suis en train d'affirmer le caractère illimité des entiers naturels, ce qui est plutôt bizarre. Car en supposant que les entiers peuvent s'écrire comme des nombres illimités, et ce serait de loin les plus nombreux, leur cardinal rejoindrait alors celui des nombres réels !
Je le vois mais je ne le crois pas.
Le nombre qu'on va tirer peut difficilement ne comporter qu'un seul chiffre, ils ne sont que 10 dans ce cas, et par rapport aux nombres à 20 chiffres par exemple, la proba est quasi nulle (10/10^20).
De même, ça peut être difficilement un des nombres à 20 chiffres, ils sont vraiment peu nombreux par rapport aux nombres à 40 chiffres.
Et ainsi de suite.....
La seule issue est que le nombre ait une infinité de chiffres. Tout nombre fini a une chance quasi nulle de sortir par rapport aux nombres illimités, car ils sont infiniment moins nombreux. Mais, je suis en train d'affirmer le caractère illimité des entiers naturels, ce qui est plutôt bizarre. Car en supposant que les entiers peuvent s'écrire comme des nombres illimités, et ce serait de loin les plus nombreux, leur cardinal rejoindrait alors celui des nombres réels !
Je le vois mais je ne le crois pas.
nodjim a écrit:Je lis dans plusieurs réponses qu'il n'est pas possible de choisir un nombre dans un ensemble, pour ce que je comprends, infini. Quelle en est la raison ?
Où vois-tu qu'il est écrit dans cette discussion qu'on ne peut pas choisir un nombre dans un ensemble infini ?? Le problème vient du caractère équiprobable du choix (répartition uniforme). Si on se fixe une autre répartition de probabilité (non uniforme), c'est complètement possible !
Par ailleurs, choisir un élément dans un ensemble infini pose des problèmes de logique pure ! Voir axiome du choix. Mais cela n'a rien à voir avec la discussion.
D'accord Léon. Maintenant, je n'ai pas trop la capacité d'aborder le difficile concept de l'axiome de choix. J'avançais simplement que le nombre sur lequel on devrait le plus probablement tombé ne peut qu'être très grand, puisque plus le nombre est grand, et mieux il est représenté. Et qu'il y aurait une contradiction flagrante à donner un max à cette taille. Et qu'on était un peu dans l'obligation d'admettre que c'étaient les nombres à taille illimitée qui prenaient le dessus. mais que ces nombres ne font pas partie de N.
nodjim a écrit: J'avançais simplement que le nombre sur lequel on devrait le plus probablement tombé (...)
Précise de manière algorithmique comment tu choisis un nombre. Après, on pourra discuter de la moyenne éventuelle, etc.
Je ne dis pas ça pour jeter un froid méprisant, non bien au contraire, c'est en fait tout le coeur du problème.
nodjim a écrit:Il me semble l'avoir dit: c'est comme si chaque entier est gravé sur un jeton, tous les jetons sont dans un sac (il est très très grand ce sac) on mélange le tout bien soigneusement et ensuite on tire un jeton au hasard.
Tu sais, moi je suis bête comme un ordinateur : le "faire comme si", je ne comprends pas. Il me faut une méthode décrite totalement...
Bah, c'est pas dur les probas et l'infini,
proba de tirer un nombre pair est:
favorables/possibles,
nombre de pairs sur nombre d'entiers.
Comme autant de pairs que d'entiers (QS bijection-cardinalité)
proba de 1 que ce nombre soit pair
et proba de 1 qu'il soit impair aussi.
Donc les entiers sont tous à la fois pairs et impairs.
Sauf si erreur sur une de mes lignes!!!
proba de tirer un nombre pair est:
favorables/possibles,
nombre de pairs sur nombre d'entiers.
Comme autant de pairs que d'entiers (QS bijection-cardinalité)
proba de 1 que ce nombre soit pair
et proba de 1 qu'il soit impair aussi.
Donc les entiers sont tous à la fois pairs et impairs.
Sauf si erreur sur une de mes lignes!!!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
95 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
