Ensemble d'entiers tels que i ne divise pas 2j

[poiuytreza]

Bonjour,

Soit un sous-ensemble de .
On suppose que pour tous et distincts de , i ne divise pas .
Montrer que
(Si on remplace par, le problème est assez classique et plus facile)
Bon courage !

[Doraki]

C'est pas 4n/9 + log4(n) +1 ?

[poiuytreza]

Euh... peut être que tu as une solution qui donne une meilleure borne (je veux bien la voir alors :happy2: ), mais en tout cas c'est l'exercice "original".

[Doraki]

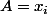
On prend un ensemble vérifiant l'hypothèse.

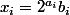
On écrit avec impair.

Les sont des nombres impairs distincts :
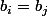
Si et si alors divise , ce qui est impossible.

On peut supposer que
Si alors on peut remplacer par 0.
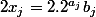
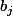
Si divise alors divise et divisait .
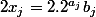
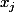
Inversement, si divise alors il divisait .

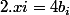
On peut supposer que
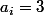
Si alors on peut remplacer par 2.
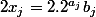
Si divise alors donc .
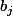
En outre, divise donc divisait .

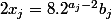
Et ainsi de suite.
On se ramène donc à un ensemble de même taille vérifiant les mêmes hypothèses, et où les sont tous pairs.

Pour tout a pair, soit .
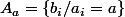
Chaque contient des nombres impairs plus petits que , ne se divisant pas deux à deux.
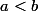
Et si alors les éléments de ne divisent pas les éléments de

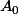
On peut supposer que les éléments de sont tous strictement supérieurs à .
En effet, si on avait x <= n/3, on pourrait alors le remplacer par 3x.
(Il faut commencer les remplacements en partant de x proche de 0 et en prenant x de plus en plus grand)

De même, on peut supposer que les éléments de sont tous strictement supérieurs à .

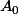
Ainsi on trouve dans au plus tous les nombres impairs entre n/3 et n. Ceci implique que .
Et de même, .

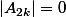
Et bien sûr, dès que n < 4^k.
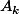
Ainsi le nombre de non vides est au plus

En sommant tout ça et en disant que [x] <= x,
.