Nombre entier
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
fma
- Membre Rationnel
- Messages: 506
- Enregistré le: 03 Mar 2013, 13:36
-
 par fma » 31 Mai 2013, 23:16
par fma » 31 Mai 2013, 23:16
Bonsoir, je n'arrive pas à démontrer un problème que je me pose :
Démontrer que pour tout entier N >200
on peut trouver x réel, tel que
si
+1/x= N)
alors
^n+1/x^n= entier)
Auriez-vous une idée ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 31 Mai 2013, 23:25
par XENSECP » 31 Mai 2013, 23:25

En posant

j'imagine qu'on peut faire des choses ?
-
fma
- Membre Rationnel
- Messages: 506
- Enregistré le: 03 Mar 2013, 13:36
-
 par fma » 31 Mai 2013, 23:35
par fma » 31 Mai 2013, 23:35
XENSECP a écrit:
En posant

j'imagine qu'on peut faire des choses ?
Oui, je suis stupide,
si par exemple

alors
^2= entier)
et
^2+(1/x)^2= entier)
car

-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 31 Mai 2013, 23:37
par XENSECP » 31 Mai 2013, 23:37
Oui aussi même si je vois pas bien où ça te mène ;)
-
fma
- Membre Rationnel
- Messages: 506
- Enregistré le: 03 Mar 2013, 13:36
-
 par fma » 31 Mai 2013, 23:40
par fma » 31 Mai 2013, 23:40
XENSECP a écrit:Oui aussi même si je vois pas bien où ça te mène

Oui, continue ta démo
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 31 Mai 2013, 23:42
par XENSECP » 31 Mai 2013, 23:42
Euh j'ai pas trouvé hein. Juste évoqué une piste de réflexion... ca donne un trinôme en X.
-
fma
- Membre Rationnel
- Messages: 506
- Enregistré le: 03 Mar 2013, 13:36
-
 par fma » 31 Mai 2013, 23:52
par fma » 31 Mai 2013, 23:52
Tous les coefficients ne sont pas forcément entiers ?
http://calculis.net/binome-newtonmais on a des couples entiers de proche en proche qui démontrent que chaque ligne suivante est entière (avec ou sans la proposition 10^4 devant x)
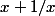

...
donc ça a l'air d'être vrai

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2013, 06:53
par chan79 » 02 Juin 2013, 06:53
fma a écrit:Bonsoir, je n'arrive pas à démontrer un problème que je me pose :
Démontrer que pour tout entier N >200
on peut trouver x réel, tel que
si
+1/x= N)
alors
^n+1/x^n= entier)
Auriez-vous une idée ?
salut
posons

et

pour n=1,

est entier
Supposons que

soit entier jusqu'à un certain rang

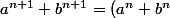(a+b)-a^n b - b^n a)
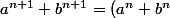(a+b)-ab(a^{n-1}+b^{n-1}))
Compte tenu des hypothèses de récurrence,

est entier car
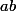
est entier
-
fma
- Membre Rationnel
- Messages: 506
- Enregistré le: 03 Mar 2013, 13:36
-
 par fma » 02 Juin 2013, 09:37
par fma » 02 Juin 2013, 09:37
chan79 a écrit:salut
posons

et

pour n=1,

est entier
Supposons que

soit entier jusqu'à un certain rang

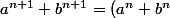(a+b)-a^n b - b^n a)
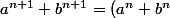(a+b)-ab(a^{n-1}+b^{n-1}))
Compte tenu des hypothèses de récurrence,

est entier car
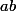
est entier
Élégante démonstration, merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités