egan a écrit:Merci pour le conseil sur TEX. ^^
En fait les deux conditions suivantes sont équivalents:
 = \lambda f(x) + \mu f(y))
 = f(x) + \lambda f(y))
Truc est envoyé sur machin veut juste dire que l'image de truc par f est machin. ^^
Pour une rotation de R^2, sa matrice est sous la forme que je t'ai indiquée si la base considérée est orthonormale.
Je pense que tu dois pouvoir vérifier sur un dessin que si tu prends comme base (0;1) et (2;0), ça ne marche plus.
--> Ah je crois avoir compris ce que tu me dit :
Si on prends un point de coordonnées
)
alors par une rotation d'angle

, l'image de ce point est
)
.
Mais comment, à partir de ça, former la matrice d'uen rotation ?
--> Et pourquoi la base doit-elle être orthonormale ?
--> J'étais en train de me demander : quel est le noyau d'une projection p.
Plaçons-nous dans l'ev
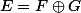
, avec
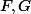
deux sev de

.
(Je ne sais pas si c'est redondant de dire " avec
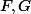
deux sev de

", si j'ai précisé avant que
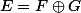
et que

est un ev).
On considère la projection

sur

parallèlement à

.
p est une application de

vers

qui, à tout

se décomposant de manière unique par
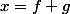
avec
\in F\times G)
, associe
=f)
.
Par définition,
 =\{x\in E , p(x)=0_E\})
.
=0_E)
équivaut à
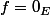
donc
=0_E\Longleftrightarrow x\in \{0_E\}\times G)
et par conséquent,
=\{0_E\}\times G = \{(0_E,g),g\in G\})
.
Es-tu d'accord avec mon raisonnement ?
--> J'ai essayé de faire la même chose avec la symétrie, je trouve
=\{0_E\})
, mais je ne suis pas à 100% sûr de mon résultat.
.
.
