Mouvement de projectile

[Rockleader]

Regarde ta donnée, relis-là, et projette.

Bon si j'ai pas compris de travers, pour A, on a donc en abscisses :

V(t) = Vo*cos(;)) ==> Z(t) = Vo*cos(;))* t

ET pour les ordonnées:

V(t) = Vo*sin(;)) - gt ==> Z(t) = Vo*sin(;))t - 1/2gt²


Est ce que c'est bien les bonnes équations horaires ?



Donc à présent, il faut lier celle de A et de B pour obtenir les conditions sur Vo et sur .

Mais, on n'a deux conditions différentes pour le projectile A, ça ne gène pas ?

[Skullkid]

Qu'est-ce que tu appelles "deux conditions différentes sur A" ?

La condition nécessaire et suffisante pour que A et B se rencontrent c'est qu'il existe un instant t0 > 0 tel que la position de A soit égale à la position de B (en prenant garde au fait que tes lois horaires ne sont valables que tant que les ordonnées sont positives, puisque les projectiles ne vont pas creuser dans le sol). À toi de traduire cette condition en une ou des conditions qui portent sur alpha et v0.

[Rockleader]

Qu'est-ce que tu appelles "deux conditions différentes sur A" ?

Ben pour A, j'ai une condition avec l'axe x et une condition avec l'axe y...

Ce qui n'est pas le cas de B.

[Mathusalem]

Ben pour A, j'ai une condition avec l'axe x et une condition avec l'axe y...

Ce qui n'est pas le cas de B.

B sur l'axe x a une condition x(t) = x_1, et sur y, celle que tu connais déjà.

T'es sûr que tu comprends bien le problème que tu es entrain de traiter ?

[Rockleader]

B sur l'axe x a une condition x(t) = x_1, et sur y, celle que tu connais déjà.

T'es sûr que tu comprends bien le problème que tu es entrain de traiter ?

Oui d'accord, mais son équation sur x vaudra toujours 0 ...




........................................................................................................


Bref, si je veux tout mettre en relation, je veux que à moment donné A et B ait les mêmes coordonnées...


Donc Il me faut:


ZxA = ZxB
ZyA= ZyB



Hors, j'ai déjà trouvé les 4 équations, donc je commence par chercher la vitesse Vo, pour ensuite en déduire l'angle Alpha ?



C'est bien la marche à suivre ?

[Mathusalem]

Oui d'accord, mais son équation sur x vaudra toujours 0 ...


Hors, j'ai déjà trouvé les 4 équations, donc je commence par chercher la vitesse Vo, pour ensuite en déduire l'angle Alpha ?



C'est bien la marche à suivre ?

Reconsidère la phrase que j'ai marqué en rouge. Tu te gourres.
Pour ce qu'il en est de la phrase en bleu : NON, il n'y a pas de 'marche à suivre'. En physique on réfléchit à un problème donné, on n'applique pas de recette, sinon on fait pas de la physique.

Le problème veut que tu trouves des conditions sur et pour que la collision ait lieu. On traduit :

On cherche les conditions sur et pour que {xA,yA} = {xB,yB}
Jusqu'à là, c'est la même condition que t'as exprimé plus haut. Cette même condition, une fois que tu as calculé les équations du mouvement, s'écrit




La première équation te dit que s'il y a collision, elle aura forcément lieu au temps

C'est le seul temps auquel les coordonnées en x de A et B seront identiques.
Donc tu sais que c'est à ce temps là seulement qu'il peut y avoir collision. En l'introduisant dans la deuxième équation, tu vas réussir à fixer le paramètre libre, en l'occurence , parce que tu vas voir ce qu'implique cette contrainte sur les autres paramètres, pour que la deuxième égalités soit satisfaite (ce que l'on impose)

implique


Donc : l'égalité des abscisses impose que le temps de collision soit
Cette contrainte introduite sur l'ordonnée te livre automatiquement qu'il y aura collision SI ET SEULEMENT SI (autrement dit que le projectile vise l'objet).

Donc là, t'as déjà ta condition sur .

Il te reste à trouver une condition sur . Mathématiquement, c'est plus dur de l'exhiber, car mathématiquement, tes équations tiennent pas compte du fait qu'une fois que l'objet touche le sol, il arrête de chuter. Donc il faut un peu interpréter physiquement le problème, et te dire qu'il faut que le projectile arrive à toucher l'objet, avant que l'objet ne tombe.
Ceci veut dire qu'il faut que le temps de collision soit inférieur au temps qu'il faut à l'objet pour chuter au sol.

Temps de chute

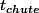
On cherche tel que

C'est-à-dire

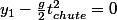
donc


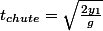AINSI Notre condition est



Donc tu as tes condition sur et sur pour qu'il y ait une collision.

[Rockleader]

Pour la phrase en rouge, effectivement, l'équation est nulle pour l'accélération et la vitesse, mais pas pour la position :marteau:




Merci de tout le temps pris pour m'aider à la compréhension de l'exercice, je sais que je peux être très "lent" à comprendre les choses parfois.


En revanche dans cet exercice, on doit rester avec des "valeurs alphabétiques", vu que l'on ne connait pas les véritables coordonnées de B ?

[Mathusalem]

Pour la phrase en rouge, effectivement, l'équation est nulle pour l'accélération et la vitesse, mais pas pour la position :marteau:




Merci de tout le temps pris pour m'aider à la compréhension de l'exercice, je sais que je peux être très "lent" à comprendre les choses parfois.


En revanche dans cet exercice, on doit rester avec des "valeurs alphabétiques", vu que l'on ne connait pas les véritables coordonnées de B ?

Remarque tout de meme, qu'en restant sous forme litterale (sans chiffres), tu donnes un aspect beaucoup plus de general a ton probleme. Maintenant, tu pourras donner l'angle alpha et la vitesse minimum pour qu'il y ait contact quelque soit {x_1,y_1} que l'on te donne, puisqu'il suffira de remplacer ces valeurs dans la formule.


Mais je voudrais m'assurer que tu as bien compris ce que tu es entrain de faire.
Est-ce que tu peux me calculer la portee d'un projectile lance depuis le sol sous un angle alpha a vitesse v0 ?

[Rockleader]

Et bien, si on a des conditions précises sur Vo et alpha je suppose que oui, suffit de remplacer.


Sinon on peut toujours déterminer la distance horizontale maximale que pourra atteindre le projectile.

On pourra par exemple imposer que le projectile ne dépasse pas plus d'une certaine hauteur ou ce genre de choses...

[Mathusalem]

Et bien, si on a des conditions précises sur Vo et alpha je suppose que oui, suffit de remplacer.


Sinon on peut toujours déterminer la distance horizontale maximale que pourra atteindre le projectile.

On pourra par exemple imposer que le projectile ne dépasse pas plus d'une certaine hauteur ou ce genre de choses...

On fixe alpha et la norme de la vitesse initiale, v0, comme dans ton probleme. A quelle distance retombe le projectile ?

[Rockleader]

Il nous suffit de remplacer par les valeurs et ainsi de trouver les coordonnées du point d’atterrissage. Et à partir de ce moment là on a la distance...

[Billball]

ah nn du tout, tu peux pas avoir le méme résultat c'est pas le méme problème..
il faut partir de F = ma et interprêter physiquement la condition de "portée"

[Rockleader]

Oui, bien évidemment, pas le même résultat qu'ici, je dis qu'il suffirait de remplacer une fois les équations horaires à nouveau calculées pour le problème donné.

[Billball]

Oui, bien évidemment, pas le même résultat qu'ici, je dis qu'il suffirait de remplacer une fois les équations horaires à nouveau calculées pour le problème donné.

soit, ce qui donne..!?

[Mathusalem]

Oui, bien évidemment, pas le même résultat qu'ici, je dis qu'il suffirait de remplacer une fois les équations horaires à nouveau calculées pour le problème donné.

Rhâââ..... Mais je veux te voir poser ces calculs ! Si tu ne fais pas l'effort de comprendre cette partie de la physique, le reste ne va être qu'un long voyage sombre... très sombre.

[Rockleader]

Rhâââ..... Mais je veux te voir poser ces calculs ! Si tu ne fais pas l'effort de comprendre cette partie de la physique, le reste ne va être qu'un long voyage sombre... très sombre.

Pardon, j'ai oublié le topic avec la rentrée...


Il y a une vitesse initiale ? Ou n'y en a t'il pas ?

[Mathusalem]

Pardon, j'ai oublié le topic avec la rentrée...


Il y a une vitesse initiale ? Ou n'y en a t'il pas ?

S'il n'y avait pas de vitesse initiale, et que l'objet est au sol... y aurait-il lieu de parler de portée ?

La vitesse initiale de l'objet est en norme, incliné d'un anlge par rapport au sol.

Montrer que la portée du projectile vaut

[Rockleader]

Je suis pas sur d'avoir compris le problème que tu me demande de la même façon que toi.


J'aurais plutôt dabord établi l'équation de la position du projectile par intégration successive.
En supposant que la position de départ se situe sur l'origine du repère.


A ce moment là si j'ai bien compris dans ton problème le Vo et l'angle alpha sont donné ?

Donc il suffit de chercher le point tel que Zprojectile = 0

Et là on mesure la distance [0;Zprojectile] et on a la portée.

[Mathusalem]

Donc il suffit de chercher le point tel que Zprojectile = 0

Je t'en prie

[Rockleader]

Je t'en prie

daccord, mais...est ce bien la marche à suivre ?