[MP] séries
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 24 Juil 2010, 07:40
par ghghgh » 24 Juil 2010, 07:40
Bonjour,
je suis en train de réfléchir sur l'exo suivant :
Existe-t-il un injection

telle que
série
}{n^2})
soit convergente ?
J'aimerais dire non car je ne vois pas d'autres moyens de faire telles injections que constante + n ou constante * n, ce qui me laissera avec une somme de série convergente + série divergente (en comportement : 1/n), donc la série serait divergente.
Mais je ne sais pas du tout comment on peut le rédiger proprement, et je n'ai pas d'idées d'arguments pour affirmer que l'injection aurait cette forme.
Merci pour toute aide

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Juil 2010, 07:41
par girdav » 24 Juil 2010, 07:41
Bonjour,
pense au critère de Cauchy.
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 24 Juil 2010, 09:19
par ghghgh » 24 Juil 2010, 09:19
Très bien, en faisant avec la négation du critère de Cauchy :
Si on peut trouver deux fonctions strictement croissante phi_1(n) et phi_2(n) : N -> N avec [TEX]\forall n \phi_{1}(n) +oo alors série des un est divergente.
Si je prends phi_1(n) = n et phi_2(n) = n^2, fonctions strictement croissantes telles que phi_1 = 1 en l'infini.
Enfin, cette injection particulière ne convient pas, mais comment le montrer pour toutes ? Peut-être qu'on peut choisir phi_1 et phi_2 (en fonction de phi) de telle manière à "compenser" phi, de manière à obtenir S_phi_2 - S_phi_1 >= k ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Juil 2010, 09:25
par girdav » 24 Juil 2010, 09:25
Si on prend

injective quelconque et que l'on note
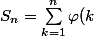}{k^2})
, comment minorer par exemple

?
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 24 Juil 2010, 09:52
par ghghgh » 24 Juil 2010, 09:52
}{(n+1)^2} + ... + \frac{\phi(2n)}{4n^2})
>=
,...,\phi(2n))}{4n^2} * n)
>=
,...,\phi(2n)}{4n})
Et comme le min des phi doit dépendre au moins de n, sinon on ne peut la construire injective...
S_2n - S_n est minorée par une constante et donc ne tend pas vers 0.
Donc il n'existe pas de phi injective de N dans N telle que la série soit convergente.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Juil 2010, 10:09
par girdav » 24 Juil 2010, 10:09
Attention, le
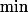
des
,\ldots,\varphi\(n^2\))
peut mal dépendre de

(si
=n^2)
par exemple).
Mais tu peux minorer autrement la différence :
\geq 1)
,
\geq 2)
etc...
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 24 Juil 2010, 10:13
par ghghgh » 24 Juil 2010, 10:13
Oui, mais ce que je voulais dire, c'est au moins de n. Que ce soit n^2, n^3, n^..., on ne tendra pas vers 0 en l'infini. phi(n) = cst*n ou cst+n est il me semble la plus petite injection de N* dans N*.
Okay pour l'autre minoration !!! :)
Du coup, S_2n - S_n >= n(n+1)/2 qui ne tend pas vers 0 en l'infini.
Donc non existence de phi.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Juil 2010, 10:22
par girdav » 24 Juil 2010, 10:22
Tu oublies de diviser par

ce qui donne que

et contredit le critère de Cauchy (puisque l'on peut prendre n'importe quel

).
édit : en fait dans ce cas même pas besoin du critère de Cauchy, puisque l'on voit que l'on ne peut pas avoir convergence de la suite des sommes partielles.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Juil 2010, 10:24
par girdav » 24 Juil 2010, 10:24
Qu'est-ce que tu entends exactement par "plus petite injection"?
-
ghghgh
- Membre Relatif
- Messages: 305
- Enregistré le: 04 Aoû 2006, 15:20
-
 par ghghgh » 24 Juil 2010, 10:32
par ghghgh » 24 Juil 2010, 10:32
Merci ! :)
Par "plus petite injection", j'entendais que l'on ne peut trouver d'injection de N dans N ayant une plus faible croissance que n, et que les autres injections seraient des O(n^a) avec a > 1.
Donc si le min était de la forme O(n^a) avec a >= 1, le rapport min / 4n
tendrait "au moins" vers une constante et sinon vers +oo en l'infini, donc dans tout les cas le critère de Cauchy ne serait pas vérifié.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
