Cactuss a écrit:Par contre pour la question 4, on nous demande d'en déduire que f est dérivable. f est bien une suite non?
Par conter si la question concernerait la série de f alors j'aurais écris:
La fonction somme d'une série entière de rayon de convergence R est continu et dérivable sur ]-R;R[
Je n'ai pas pu répondre avant, j'ai une rupture de courant et le courant vient juste de revenir, mon onduleur n'a pas tenu assez longtemps pour pouvoir répondre.
L'exercice proposé était l'étude d'une série entière et f(x) était la somme de cette série entière et toutes les questions posées se rapportaient à la série entière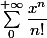 
et non è suite de fonctions = \dfrac{x^n}{n!})
Tu as dit que le rayon de cette série entière est
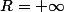
, ce qui est exact et donc la suite de fonctions
converge vers 0.
J'ajouterai même dans le cas général:
La somme d'une série entière de rayon de convergence
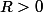
est une fonction de classe
sur
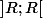
dont les dérivées sont les sommes des dérivées correspondantes du terme général.
De plus la série entière et les séries entières des dérivées sont des séries normalement convergentes sur ttout intervalle fermé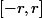 
avec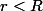 
Remarque:Tu as écrit quelque chose d'erroné dans un de tes précédents message. C'était
On sait que
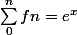
alors qu'il fallait écrire
=e^x)
, chose que tu ne pouvais pas faire,
c'était le but de l'exerciceVu ton 1er message, tu as intérêt à revoir le cours surs les séries.
