Point critique

par **nivéa** » 21 Aoû 2008, 01:02

xyz1975 a écrit:Tout est bon, je pense que vous avez trouvé la même chose que moi.
Il suffit de résoudre le système suivant :

Soit

soit

est ce que c'est bon?

ce qui vous a permis de passer d'une écriture à une autres c'est le fait de dire que : e^-(x²+y²) est différent de zéro.

par **xyz1975** » 21 Aoû 2008, 01:03

nivéa a écrit:j'ai trouvé la même chose que vous, depuis toute à l'heure je ne trouvais pas ou je m'était trompée, je n'arrivais pas à comprendre.

Maintenant, j'ai trouvé la même chose que vous, j' y suis arrivée.

Si

On remplace dans la deuxième équation on trouve deux valeurs de y ce qui nous donne deux couples.
De même pour

par **xyz1975** » 21 Aoû 2008, 01:04

nivéa a écrit:ce qui vous a permis de passer d'une écriture à une autres c'est le fait de dire que : e^-(x²+y²) est différent de zéro.

Oui c'est bien ça.

par **nivéa** » 21 Aoû 2008, 01:12

xyz1975 a écrit:Si
On remplace dans la deuxième équation on trouve deux valeurs de y ce qui nous donne deux couples.
De même pour

oui si on prend ici

et on la remplace dans l'equation (2) : x(1-2y²)=0, on trouve trouve alors
y = 1/(2)^1/2
et y = -1/(2)^1/2

par **xyz1975** » 21 Aoû 2008, 01:17

nivéa a écrit:oui si on prend ici
et on la remplace dans l'equation (2) : x(1-2y²)=0, on trouve trouve alors
y = 1/(2)^1/2
et y = -1/(2)^1/2

Mais plûtot ou, dans ce cas les couples suivants

et

vérifient le système.
On trouve de même pour la valeur -

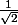
de x les couples suivants :

et

On a en total 4 solutions.
N'oubliez pas que pour une valeur de x on deux valeurs possibles de y ce qui fait deux couples solutions.

par **nivéa** » 21 Aoû 2008, 01:27

je pense que c'est la fatigue qui me joue des tours.

nous avons vu que
1) quand y=0, on trouvais
x=y=0

2) quand y est différent de 0
x=1/(2)^1/2 et x=-1/(2)^1/2

3) si x=1/(2)^1/2
y=1/(2)^1/2 et y=-1(2)^1/2

c'est ca.

par **nivéa** » 21 Aoû 2008, 01:31

oui, je trouve exactement la même chose que vous, je pense que c'est la fatigue!!! :we:

Merci.

par **xyz1975** » 21 Aoû 2008, 01:38

nivéa a écrit:oui, je trouve exactement la même chose que vous, je pense que c'est la fatigue!!! :we:

Merci.

Certainement, bon est ce que l'idée générale est aquise?

Première étape : On factorise au maximum les expressions du système.
Deuxième étape : On résout la première équation (ou celle que vous jugez simple) on procède alors par séparation des cas.

par **nivéa** » 21 Aoû 2008, 01:49

xyz1975 a écrit:Certainement, bon est ce que l'idée générale est aquise?

Première étape : On factorise au maximum les expressions du système.
Deuxième étape : On résout la première équation (ou celle que vous jugez simple) on procède alors par séparation des cas.

oui, l'idée général est acquise, merci.

par **nivéa** » 21 Aoû 2008, 01:51

mais une petite question, histoire d'être bien sûr quand vous dite "on procède alors par séparation des cas" c'est que l'on utilise la variable y ou x différent ou égale à zéro, comme vous l'avez fait ultérieurement dans la démonstration.

comme vous avez procédé ci-dessous:

Premier cas

:
Que devient le système?
0=0 qui est toujours vraie.
x=0.

on a supposé que y=0 et on a trouvé x=0 donc on a comme solution le couple (0;0).

Deuxième cas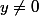

Dans ce cas c'est 1-2x² qui est nul ce qui donne deux valeurs à x.
Remplacez maintenant dans la deuxième équation et donnez moi les solutions.[/quote]

par **xyz1975** » 21 Aoû 2008, 01:59

Puisque vous avez factorisez l'expression donnant l'équation, forcément alors cela conduit à une séparation des cas.
Je ne peux pas donner une méthode générale car on n'a pas une forme régulière mais d'une manière générale c'est comme ça qu'on procède.
Dommage que l'outil "logique mathématique" simplifie énnormément la tâche.

par **xyz1975** » 21 Aoû 2008, 02:07

Vous voulez continuez ou c'est la fatigue? il est clair que la fonction de départ admet un seul point critique c'est bien l'origine (0;0).

par **nivéa** » 21 Aoû 2008, 02:15

merci pour les explication, je suis en plein calcul de la matrice hessienne.

J'en trouve une de la forme suivante
Hf= 1/2

par **nivéa** » 21 Aoû 2008, 02:26

je voudrai en faite une confirmation de votre part, pour calculer ma matrice hessienne, il faut considérer l'exposant comme différent de zéro, cela entrain à étudier la matrice à partir de l'équation suivante:

y

x

merci.

par **xyz1975** » 21 Aoû 2008, 02:36

nivéa a écrit:merci pour les explication, je suis en plein calcul de la matrice hessienne.

J'en trouve une de la forme suivante
Hf= 1/2

d'où vient le 1/2

Par définition :

nivéa a écrit:je voudrai en faite une confirmation de votre part, pour calculer ma matrice hessienne, il faut considérer l'exposant comme différent de zéro, cela entrain à étudier la matrice à partir de l'équation suivante:

y
x

merci.

J'ai pas compris?

par **nivéa** » 21 Aoû 2008, 02:41

la matrice est écrite sous la forme quadrature c'est pour cela qu'il y a le 1/2

si je ne me trompe pas

par **xyz1975** » 21 Aoû 2008, 02:49

La matrice hessienne c'est bience que vous avez trouvé mais sans le facteur 1/2. La définition est claire, valable pour toute fonction dont les dérivées partielles secondes existent.
je suis vraiment désolé je vais quitter à demain. bonne continuation.

par **nivéa** » 21 Aoû 2008, 02:50

xyz1975 a écrit:La matrice hessienne c'est bience que vous avez trouvé mais sans le facteur 1/2. La définition est claire, elle est valable pour toute fonction dont les dérivées partielle secondes existent.
je suis vraiment désolé je vais quitter à demain. bonne continuation.

merci pour votre aide, à demain. :we:

Point critique

point critique

point critique

matrice hessienne

matrice hessienne

matrice hessienne

Qui est en ligne