Point critique
38 messages
- Page 1 sur 2 - 1, 2
point critique
je suis actuellement entrain de faire un exos sur le point critique:
soit f(x,y)=x^5y + xy^5 + xy
1) j'ai calculé les dérivées partielles (ici le d est un d rond)
df/dx = 5yx^4 + y^5 + y =>y(5x^4 + y^4 + 1)
df/dy = x^5 + 5xy^4 + x =>x(5y^4 + x^4 + 1)
2) j'ai calculé les dérivées secondes
d²f/dx² = 20yx^3
d²f/dy² = 20xy^3
d²f/dxdy = 5x^4 + 5y^4 + 1
d²f/dydx = 5x^4 + 5y^4 + 1
3) la je suis pas sur
df = df/dx + df/dy = 0
donc x=y=0
4) matrice hessienne
Hf = 1/2 ( 0 1 )
( 1 0 )
Là je suis perdu pour déterminer le point critique je suis pas sur de moi, de plus il faut aussi déterminer si la hessienne est positif, négatif ou non-défini ou dégénérée.
Pourriez-vous me dire comme m'y prendre pour m'assurer de toujours trouver les points critiques d'une fonction.
Merci. :we:
soit f(x,y)=x^5y + xy^5 + xy
1) j'ai calculé les dérivées partielles (ici le d est un d rond)
df/dx = 5yx^4 + y^5 + y =>y(5x^4 + y^4 + 1)
df/dy = x^5 + 5xy^4 + x =>x(5y^4 + x^4 + 1)
2) j'ai calculé les dérivées secondes
d²f/dx² = 20yx^3
d²f/dy² = 20xy^3
d²f/dxdy = 5x^4 + 5y^4 + 1
d²f/dydx = 5x^4 + 5y^4 + 1
3) la je suis pas sur
df = df/dx + df/dy = 0
donc x=y=0
4) matrice hessienne
Hf = 1/2 ( 0 1 )
( 1 0 )
Là je suis perdu pour déterminer le point critique je suis pas sur de moi, de plus il faut aussi déterminer si la hessienne est positif, négatif ou non-défini ou dégénérée.
Pourriez-vous me dire comme m'y prendre pour m'assurer de toujours trouver les points critiques d'une fonction.
Merci. :we:
point critique
xyz1975 a écrit:Bonjour,
Un point critique est par définition le point qui annule le gradiant ce qui revient donc à résoudre un système.
Dans votre cas vous avez calculé les deux dérivées partielles (par rapport à x et à y) il suffit d'égaliser le tout à zéro. c'est bien ce que vous avez trouvé (0;0).
Merci.
Dans un de mes exo il se trouve qu'on a plusieurs points critiques, comme on fait pour les trouver? moi j'en trouve tjs un, c'est pas normal !!!
point critique
xyz1975 a écrit:Ceci dépend de la résolution du système en question, certainement vous avez oublié de séparer les cas. donnez nous un exemple si vous voulez.
Merci,
pour cet exemple j'ai essayé de le faire mais je n'ai qu trouver une seul solution (0,0)
donc, soit f(x,y) = xy exp(-(x²+y²))
1) trouver tous les pts critiques de la fonction dans IR².
point critique
xyz1975 a écrit:Tout est bon, je pense que vous avez trouvé la même chose que moi.
Il suffit de résoudre le système suivant :
Soitsoit
est ce que c'est bon?
oui je trouve la même chose que vous, mais le seul soucis reste que je n'arrive pas a savoir comment vous trouver 5 points critiques.
Dans ce genre de système il n'y a pas de régle générale car le système n'est pas particulier c'est à dir n'a pas de forme générale donc pas de régle générale. il suffit de résoudre par séparation des cas.
Je ne veux pas alourdir l'exposé, en fait la logique mathématique est le seul moyen pour JUSTIFIER et trouver rapidement l'ensemble de toutes les solutions en une ligne, une chose que je suis incapable de faire ici.
Bref l'unique méthode pour ce système est la séparation des cas, j'explique, je vous conseille d'abord de TOUT FACTORISER c'est bien notre cas.
Ensuite égaliser chaque terme à zéro dans la première équation et voir ce qui se passe dans la deuxième.
Premier cas :
:
Que devient le système?
0=0 qui est toujours vraie.
x=0.
on a supposé que y=0 et on a trouvé x=0 donc on a comme solution le couple (0;0).
Deuxième cas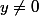
Dans ce cas c'est 1-2x² qui est nul ce qui donne deux valeurs à x.
Remplacez maintenant dans la deuxième équation et donnez moi les solutions.
Je ne veux pas alourdir l'exposé, en fait la logique mathématique est le seul moyen pour JUSTIFIER et trouver rapidement l'ensemble de toutes les solutions en une ligne, une chose que je suis incapable de faire ici.
Bref l'unique méthode pour ce système est la séparation des cas, j'explique, je vous conseille d'abord de TOUT FACTORISER c'est bien notre cas.
Ensuite égaliser chaque terme à zéro dans la première équation et voir ce qui se passe dans la deuxième.
Premier cas
Que devient le système?
0=0 qui est toujours vraie.
x=0.
on a supposé que y=0 et on a trouvé x=0 donc on a comme solution le couple (0;0).
Deuxième cas
Dans ce cas c'est 1-2x² qui est nul ce qui donne deux valeurs à x.
Remplacez maintenant dans la deuxième équation et donnez moi les solutions.
xyz1975 a écrit:Dans ce genre de système il n'y a pas de régle générale car le système n'est pas particulier c'est à dir n'a pas de forme générale donc pas de régle générale. il suffit de résoudre par séparation des cas.
Je ne veux pas alourdir l'exposé, en fait la logique mathématique est le seul moyen pour JUSTIFIER et trouver rapidement l'ensemble de toutes les solutions en une ligne, une chose que je suis incapable de faire ici.
Bref l'unique méthode pour ce système est la séparation des cas, j'explique, je vous conseille d'abord de TOUT FACTORISER c'est bien notre cas.
Ensuite égaliser chaque terme à zéro dans la première équation et voir ce qui se passe dans la deuxième.
Premier cas:
Que devient le système?
0=0 qui est toujours vraie.
x=0.
on a supposé que y=0 et on a trouvé x=0 donc on a comme solution le couple (0;0).
Deuxième cas
Dans ce cas c'est 1-2x² qui est nul ce qui donne deux valeurs à x.
Remplacez maintenant dans la deuxième équation et donnez moi les solutions.
dans notre cas ici y est différent de 0
donc on a : 1 -2x²=0 =>x= (1/2)^1/2
point critique
xyz1975 a écrit:Mais NON!!!
1-2x²=0 équivaut à x²=1/2 soit
oui pardon, erreur d'écriture. je viens de prendre connaissance du logiciel latex et je suis entrain d'essayer d'écrire avec.
Merci
xyz1975 a écrit:ça doit être une erreur de calcu, n'oubliez pas que
x et y jouent un rôle symétrique donc
Je vais refaire encore une fois le calcul mais je pense que c'est ça.
j'ai trouvé la même chose que vous, depuis toute à l'heure je ne trouvais pas ou je m'était trompée, je n'arrivais pas à comprendre.
Maintenant, j'ai trouvé la même chose que vous, j' y suis arrivée.
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
