Point critique
86 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Re: point critique
Pour votre réponse, elle diffère de la mienne: j'ai trouvé 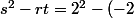 (-6) = 4 - 12 = - 8 < 0)
et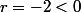 , donc on a un maximum local , n'est - ce pas ?
, donc on a un maximum local , n'est - ce pas ?
et
Re: point critique
donc pour (1,1) c'est un maximum global global et (-1/3,-1/3) un minimum local ou un col ??
Re: point critique
Pour votre question
veuillez regarder ici .selda6958 a écrit:oui mais je comprend pas pourquoi c'est local ?
Re: point critique
selda6958 a écrit:un maximum en -1/3 pardon
On dit ici un extremum en un point (a,b) .
En
Re: point critique
oui donc un col en (-1/3;-1/3) car vous m'avez dit un maximum local
et on a un maximum global en (1,1) ?
et on a un maximum global en (1,1) ?
Re: point critique
Non, pour (1,1) j'ai dit
et ce n'est pas un maximum global car f(0,-10) = 990 > f(1,1) = 1,
et pour) c'est bien un col : regarder la preuve dans mon post
c'est bien un col : regarder la preuve dans mon post
aymanemaysae a écrit:Pour votre réponse, elle diffère de la mienne: j'ai trouvé
et, donc on a un maximum local , n'est - ce pas ?
et ce n'est pas un maximum global car f(0,-10) = 990 > f(1,1) = 1,
et pour
aymanemaysae a écrit:Pouron a bien un col :
(-\frac{1}{3}, -\frac{1}{3} ) = \left\(\begin{pmatrix}-2&2\\2&2\end{pmatrix})
doncet
, donc c'est un col .
Re: point critique
dac merci et du coup pour ma fonction je n'arrive pas à résoudre le système :
4y-4x^3=0
4x-4y^3=0
4y-4x^3=0
4x-4y^3=0
Re: point critique
Pour  = 4 xy - x^4 - y^4) , on a
, on a  = 4 y - 4 x^3)
et comme les variables x et y jouent le même rôle dans h(x,y) , on a = 4 x - 4 y^3) ,
,
donc = 0 \\\frac{\partial h}{\partial y}(x,y) = 0 \end{matrix}) \right arrow
\right arrow 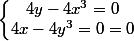 ,
,
maintenant dîtes-moi ce que vous avez fait, et on verra pour la suite.
et comme les variables x et y jouent le même rôle dans h(x,y) , on a
donc
maintenant dîtes-moi ce que vous avez fait, et on verra pour la suite.
Re: point critique
M. Chan79 vous a montré le chemin.
donc = 0 \\\frac{\partial h}{\partial y}(x,y) = 0 \end{matrix}) \right arrow
\right arrow 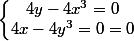 , [/tex] \right arrow
, [/tex] \right arrow 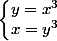 .
.
En substituant dans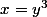 , y par son expression en fonction de x vous aurez
, y par son expression en fonction de x vous aurez 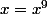 , donc
, donc 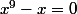 , donc
, donc  = 0) : en utilisant l'identité remarquable
: en utilisant l'identité remarquable 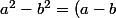(a + b)) vous arriverez à destination.
vous arriverez à destination.
Essayez un peu et on verra .
donc
En substituant dans
Essayez un peu et on verra .
Re: point critique
M. Zygomatique a presque donné la factorisation de  :
:
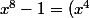^2 - 1^2 = (x^4 - 1)(x^4 + 1) = ((x^2)^2 - 1)(x^4 + 1) = (x^2 - 1)(x^2 + 1)(x^4 + 1))
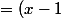 (x + 1) (x^2 + 1) (x^4 + 1)) , les termes
, les termes  et
et  ne s'annulent pas dans
ne s'annulent pas dans  ,
,
donc = x (x - 1) (x + 1) (x^2 + 1) (x^4 + 1)) .
.
Vous pouvez continuer maintenant.
donc
Vous pouvez continuer maintenant.
Re: point critique
Je crois que vous êtes fatigué maintenant: je donne les points critiques et on continuera demain si vous voulez bien.
On a = x (x - 1) (x + 1) (x^2 + 1) (x^4 + 1)) , donc
, donc  = 0) donne bien que x=0 ou x = 1 ou x = - 1.
donne bien que x=0 ou x = 1 ou x = - 1.
Et comme on a , donc pour x = 0 on aura y = 0, pour x = 1 on aura y = 1 et pour x = - 1 on aura y = - 1,
, donc pour x = 0 on aura y = 0, pour x = 1 on aura y = 1 et pour x = - 1 on aura y = - 1,
donc les points critiques sont : (0,0) , (1,1) et (-1,-1) .
Bonne nuit.
On a
Et comme on a
donc les points critiques sont : (0,0) , (1,1) et (-1,-1) .
Bonne nuit.
Re: point critique
salut
du coup en ayant fait les calculs pour ma fonction :
en (0,0) on a un col
en, (1,1) on a un maximum global
en (-1,-1) on a un minimum global
du coup en ayant fait les calculs pour ma fonction :
en (0,0) on a un col
en, (1,1) on a un maximum global
en (-1,-1) on a un minimum global
86 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
