Point critique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 18:29
par nivéa » 27 Aoû 2008, 18:29
bonjour à tous,
je suis sur un exercice et je n'arrive pas à trouver mon erreur.
Soit f(x,y)=

1) montrer que (0,0) , (
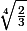
,-
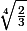
) , (-
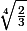
,
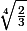
)
Ce que je n'arrive pas à avoir c'est la puissance 4 de la racine, je m'obtient que la puissance 3.
Pourriez-vous m'aider à trouver ma faute.
Merci.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 19:06
par leon1789 » 27 Aoû 2008, 19:06
nivéa a écrit:1) montrer que (0,0) , (
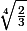
,-
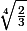
) , (-
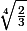
,
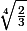
)
Heu, montrer que quoi ?
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 19:13
par nivéa » 27 Aoû 2008, 19:13
Alors, ici le problème ce pose qu'il faut montrer que les trois points critique que j'ai cité en amont sont les seuls points critique de la fonction.
-
Black Jack
 par Black Jack » 27 Aoû 2008, 19:26
par Black Jack » 27 Aoû 2008, 19:26
Condition nécessaire pour avoir des point critiques en (X ; Y) :
La dérivée première partielle de f(x,y) par rapport à x au point considéré = 0 et la dérivée première partielle de f(x,y) par rapport à y au même point = 0
En exprimant ces conditions, on obtient un système de 2 équations avec 3 couples solutions (et ce sont effectivement les couples donnés dans l'énoncé).
:zen:
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 19:31
par nivéa » 27 Aoû 2008, 19:31
Black Jack a écrit:Condition nécessaire pour avoir des point critiques en (X ; Y) :
La dérivée première partielle de f(x,y) par rapport à x au point considéré = 0 et la dérivée première partielle de f(x,y) par rapport à y au même point = 0
En exprimant ces conditions, on obtient un système de 2 équations avec 3 couples solutions (et ce sont effectivement les couples donnés dans l'énoncé).
:zen:
Pourriez-vous me détailler vos calcules pour voir ou se situe mon erreur.
Merci.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 19:35
par nivéa » 27 Aoû 2008, 19:35
bonjour,
soit f(x,y)=
 1) calcul des dérivées partielles:
1) calcul des dérivées partielles:df/dx=2x+3x²y^3 d²f/dx²=2+6xy^3
df/dy=2y+3y²x^3 d²f/dy²=2+6yx^3
d²f/dxdy=d²f/dydx= 9x²y²
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 20:32
par nivéa » 27 Aoû 2008, 20:32
après avoir calculé les dérivées partielles, je cherche les points critiques de cette fonction:
premier cas y=0 (1):
=0)
(2):
=0)
donc : (1):2x=0 =>
x=y=0 deuxième cas y#0 (1):
=0)
(2):
=0)
d'où: (2):

=>

=>
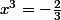
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Aoû 2008, 20:35
par Doraki » 27 Aoû 2008, 20:35
Pourquoi t'es passé de 2+3yx³ à 2+3x³ ?
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 20:42
par nivéa » 27 Aoû 2008, 20:42
Doraki a écrit:Pourquoi t'es passé de 2+3yx³ à 2+3x³ ?
car nous sommes dans le cas ou y#0:
=0)
donc, j'élimine tous les y, et c'est pour cela que je me retrouve avec l'expression suivantes qui est : 2+3x^3=0
je ne suis pas sur de moi, c'est pour cela que je demande!!
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 21:55
par nivéa » 27 Aoû 2008, 21:55
nivéa a écrit:après avoir calculé les dérivées partielles, je cherche les points critiques de cette fonction:
premier cas y=0 (1):
=0)
(2):
=0)
donc : (1):2x=0 =>
x=y=0 deuxième cas y#0 (1):
=0)
(2):
=0)
d'où: (2):

=>

=>
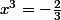
mon erreur de situe là:
2):

=>
=>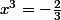 [/quote]
[/quote]je l'ai pu le constater grâce à un coup de main:
(1):
=0)
(2):
=0)
je considère x#0
(1):2+3xy^3=0 =>x=-2/3y^3
on remplace (1) dans (2):
La deuxième de vient :
y
)
=0
Il est clair que y\neq0 car dans ce cas x sera aussi nul, écartons alors ce cas il nous reste l'autre partie :
2-

=0
On réduit au même dénominateur :

Soit :
18y^8-8=0

On passe à la racine carrée
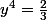
attention on prends pas la valeur négative -2/3 car y^4 est toujours positif.
Finalement on compose avec la racine quatrième on trouve :
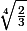
ou
-
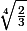
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 22:31
par nivéa » 27 Aoû 2008, 22:31
je trouvé la solution de la matrice hessienne au point critique (0,0)
r=d²f/d²x t=d²f/d²y s=d²f/dxdy=d²f/dydx

je rappelle que la fonction
=x^2+y^2+x^3y^3)
donc: r=2 t=2 et s=0
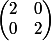
je détermine le déterminant de la matrice hessienne
soit:
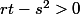
donc: (2*2)>0
à part de ça, j"en déduis donc que la valeurs propres de la matrice hessienneest
strictement postive de f en (0,0)et elle est définie positive donc (0,0) est un mini. local
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:40
par juve1897 » 27 Aoû 2008, 23:40
As tu fini de résoudre ton exercice ???
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 23:51
par nivéa » 27 Aoû 2008, 23:51
Non, je n'arrive pas à trouver les deux solutions de la matrice hessienne avec les deux points critiques.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:53
par juve1897 » 27 Aoû 2008, 23:53
nivéa a écrit:Non, je n'arrive pas à trouver les deux solutions de la matrice hessienne avec les deux points critiques.
Je suis désolée je ne pourrais pas t'aider, je n'y connais pas grand chose.
Cependant, je pense que d'autre personne seront en mesure de te répondre.
J'espere que tu trouveras qqun pour t'aider .
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 00:32
par nivéa » 28 Aoû 2008, 00:32
soit f(x,y)=

les points critique sont les suivants:
 , (\sqrt[4]{\frac 23},- \sqrt[4]{\frac 23}) , (- \sqrt[4]{\frac 23} ,\sqrt[4]{\frac 23} ))
je n'arrive qu'à trouver la matrice au point (0,0)!!
y aurai t-il qqun pour me mettre sur la voix.
Merci.
-
charlol
- Membre Naturel
- Messages: 66
- Enregistré le: 29 Juin 2008, 11:33
-
 par charlol » 28 Aoû 2008, 00:36
par charlol » 28 Aoû 2008, 00:36
Salut ,
Je ne vois pas non plus comment tu te débarasse du y dans 2+3yx³
si yIR* y( 2+3yx³)=0 => 2+3yx³ =0 on est d'accord , mais après je pense que tu t'es trompé
Charlol
-
Black Jack
 par Black Jack » 28 Aoû 2008, 16:43
par Black Jack » 28 Aoû 2008, 16:43
nivéa,
Ton message 10 est correct.
En (0;0), j'arrive aussi à un minimum de f(x,y)
Pour les 2 autres cas, j'arrive à rt - s² < 0
Et donc f(x,y) n'a ni minimum ni maximum en ces points.
:zen:
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 17:18
par nivéa » 28 Aoû 2008, 17:18
Black Jack a écrit:nivéa,
Ton message 10 est correct.
En (0;0), j'arrive aussi à un minimum de f(x,y)
Pour les 2 autres cas, j'arrive à

Et donc f(x,y) n'a ni minimum ni maximum en ces points.
:zen:
Bonjour,
ce que j'aimerai savoir c'est comment vous vous y étiez pris pour trouver un

. pourriez-vous détailler votre démarche, j'ai essayé mais je n'arrive pas à y aboutir.
Merci.
-
Black Jack
 par Black Jack » 28 Aoû 2008, 18:04
par Black Jack » 28 Aoû 2008, 18:04
Sauf erreur on trouve:
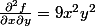
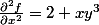
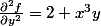
Et pour les cas
)
et
)
On arrive à
^2 < 0)
Vérifie et fais le calcul ...
:zen:
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 18:23
par nivéa » 28 Aoû 2008, 18:23
Black Jack a écrit:Sauf erreur on trouve:
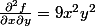
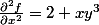
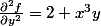
Et pour les cas
)
et
)
On arrive à
^2 < 0)
Vérifie et fais le calcul ...
:zen:
je pense que vous vous trompez(sauf erreur de ma part)
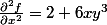
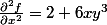
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
