Séries entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 00:06
par mehdi-128 » 24 Nov 2007, 00:06
Bonsoir ,je n'arrive point a calculer la somme suivante:
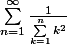
merci ....
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2007, 01:01
par yos » 24 Nov 2007, 01:01
Bonsoir.
Ce n'est pas une série entière.
Utilise le calcul classique de la somme des carrés des n premiers entiers naturels. Ensuite tu peux décomposer en éléments simples la fraction obtenue.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 01:06
par mehdi-128 » 24 Nov 2007, 01:06
yos a écrit:Bonsoir.
Ce n'est pas une série entière.
Utilise le calcul classique de la somme des carrés des n premiers entiers naturels. Ensuite tu peux décomposer en éléments simples la fraction obtenue.
Justement tout ca je l'ai fait mais jobtiens :
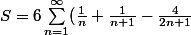)
et la je suis bloqué ....
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2007, 01:19
par yos » 24 Nov 2007, 01:19
Travaille avec la somme partielle d'ordre n.
=1+1/(n+1)+4\sum_2^n 1/(2k))
,
...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 01:50
par mehdi-128 » 24 Nov 2007, 01:50
yos a écrit:Travaille avec la somme partielle d'ordre n.
=1+1/(n+1)+4\sum_2^n 1/(2k))
,
...
Désolé mais je vois pas d'ou sort l'égalité ......
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 09:52
par mehdi-128 » 24 Nov 2007, 09:52
Quelqu'un pourrait-il m'aider ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Nov 2007, 09:56
par tize » 24 Nov 2007, 09:56
Bonjour,
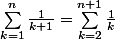
donc
=...)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 10:06
par mehdi-128 » 24 Nov 2007, 10:06
tize a écrit:Bonjour,
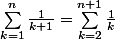
donc
=...)
merci mais je vois pas comment continuer après et à quoi va me servir ce résultat ....
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Nov 2007, 10:11
par tize » 24 Nov 2007, 10:11
bon...
=\sum_1^n 1/k+\sum_2^{n+1} 1/k=1+\(\sum_2^n 1/k\)+\(\sum_2^n 1/k\)+1/(n+1)=...)
on pourrait aussi dire ça se voit...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 10:50
par mehdi-128 » 24 Nov 2007, 10:50
tize a écrit:bon...
=\sum_1^n 1/k+\sum_2^{n+1} 1/k=1+\(\sum_2^n 1/k\)+\(\sum_2^n 1/k\)+1/(n+1)=...)
on pourrait aussi dire ça se voit...
oui mais je vois pas l'utilité de faire ça je n'arrive toujours pas a déterminer la limite ...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Nov 2007, 11:01
par tize » 24 Nov 2007, 11:01
=1+1/(n+1)+4\sum_2^n 1/(2k))
donc
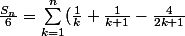=1+1/(n+1)+4\sum_2^n 1/(2k)-\sum_{k=1}^{n}\frac{4}{2k+1}=\frac{3}{2}+1/(n+1)+4\sum\limits_{k=1}^{2n+1}\frac{(-1)^k}{k})
ona fait apparaitre une série classique...
aux erreurs de calculs près...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 11:12
par mehdi-128 » 24 Nov 2007, 11:12
+4\sum_2^n 1/(2k)-\sum_{k=1}^{n}\frac{4}{2k+1}=\frac{3}{2}+1/(n+1)+4\sum\limits_{k=1}^{2n+1}\frac{(-1)^k}{k})
[\TEX ]
je comprends pas ce passage .....
merci ....
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 11:40
par mehdi-128 » 24 Nov 2007, 11:40
C'est la somme avec le (-1)^k qui me trouble je vois pas d'ou elle sort :marteau:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2007, 12:12
par yos » 24 Nov 2007, 12:12
Salut Tize et merci.
Pour Mehdi : (somme des inverses des pairs) moins (somme des inverses des impairs) = somme alternée des inverses de ces entiers.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 12:25
par mehdi-128 » 24 Nov 2007, 12:25
yos a écrit:Salut Tize et merci.
Pour Mehdi : (somme des inverses des pairs) moins (somme des inverses des impairs) = somme alternée des inverses de ces entiers.
euh pourtant j'écris les sommes je vois pas trop d'ou sort le résultat .... :marteau:(et je vois pas d'ou sort le 3/2) :briques:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2007, 13:02
par yos » 24 Nov 2007, 13:02
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 13:06
par mehdi-128 » 24 Nov 2007, 13:06
yos a écrit: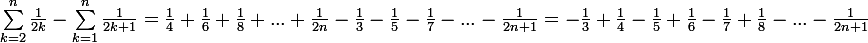
Ah merci beaucoup ......
C'est donc égal a :
^k}{k})
?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 13:33
par mehdi-128 » 24 Nov 2007, 13:33
Je trouve 2-24.ln(2) ca vous semble bon ou pas ?
merci d'avance ....
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Nov 2007, 13:49
par ThSQ » 24 Nov 2007, 13:49
mehdi-128 a écrit:Je trouve 2-24.ln(2) ca vous semble bon ou pas ?
merci d'avance ....
Plutôt -ln(2) + 1 -1/2 il me semble bien
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 24 Nov 2007, 13:56
par mehdi-128 » 24 Nov 2007, 13:56
ThSQ a écrit:Plutôt -ln(2) + 1 -1/2 il me semble bien
hein euh c'est bizarre car j'ai vérifié mon calcul 3 faois je pense pas avoir d'erreurs ..... :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
