Intégrales suites
15 messages
- Page 1 sur 1
Intégrales suites
Bonjour
On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] =[tex]\int_0^1\sqrt{1-t^2}dt[/tex] et I[sub]n[/sub]=[tex]\int_0^1t^n\sqrt{1-t^2}dt[/tex] pour tout n€IN
1)on pose f(x)=[tex]\int_0^{cosx }\sqrt{1-t^2}dt[/tex] pour tout x€IR
a)Montrer que f est derivable sur IR puis calculer f'(x)
b) Déterminer f(x) pour x€[[tex]0; \frac{\pi}{2}[/tex]] puis en déduire la valeur de I[sub]0[/sub]
c) Interpréter graphiquement l'integrale I[sub]0[/sub] et retrouver sa valeur
2)a) Montrer que la suite (I[sub]n[/sub])est décroissante et minoré. Que peut-on en deduire ?
b) Montrons que pour tout n€IN ; 0<=I[sub]n[/sub]<=[tex]\frac{1}{n+1}[/tex] puis en déduire lim(I[sub]n[/sub]) en +oo
3)a) calculer I[sub]1[/sub]
b) À l'aide d'une intégration par parties , montrer que pour tout n€IN ; I[sub]n+2[/sub]=[tex]\frac{n+1}{n+4}I_n[/tex].
c) Montrer que pour tout n€IN ;
[tex]\frac{n+1}{n+4}[/tex]<=[tex]\frac{I_{n+1}}{I_n}[/tex]<=1 puis calculer lim([tex]\frac{I_{n+1}}{I_n}[/tex]) en +oo
4)a)Montrer par récurrence que pour tout n€IN ; I[sub]n[/sub]*I[sub]n+1[/sub]=[tex]\frac{\pi}{2(n+1)(n+2)(n+3)}[/tex]
b) prouver que lim(n[tex]\sqrt{n}I_n[/tex])=[tex]\sqrt{\frac{\pi}{2}}[/tex]
5) Montrer que [tex]I_{2n}=\frac{(2n)! \pi}{2^{2n+2}n ! (n+1)! }[/tex] et en déduire l'expression de I[sub]2n+1[/sub]
Pouvez vous me donner des indices pour ses questions ?
On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] =[tex]\int_0^1\sqrt{1-t^2}dt[/tex] et I[sub]n[/sub]=[tex]\int_0^1t^n\sqrt{1-t^2}dt[/tex] pour tout n€IN
1)on pose f(x)=[tex]\int_0^{cosx }\sqrt{1-t^2}dt[/tex] pour tout x€IR
a)Montrer que f est derivable sur IR puis calculer f'(x)
b) Déterminer f(x) pour x€[[tex]0; \frac{\pi}{2}[/tex]] puis en déduire la valeur de I[sub]0[/sub]
c) Interpréter graphiquement l'integrale I[sub]0[/sub] et retrouver sa valeur
2)a) Montrer que la suite (I[sub]n[/sub])est décroissante et minoré. Que peut-on en deduire ?
b) Montrons que pour tout n€IN ; 0<=I[sub]n[/sub]<=[tex]\frac{1}{n+1}[/tex] puis en déduire lim(I[sub]n[/sub]) en +oo
3)a) calculer I[sub]1[/sub]
b) À l'aide d'une intégration par parties , montrer que pour tout n€IN ; I[sub]n+2[/sub]=[tex]\frac{n+1}{n+4}I_n[/tex].
c) Montrer que pour tout n€IN ;
[tex]\frac{n+1}{n+4}[/tex]<=[tex]\frac{I_{n+1}}{I_n}[/tex]<=1 puis calculer lim([tex]\frac{I_{n+1}}{I_n}[/tex]) en +oo
4)a)Montrer par récurrence que pour tout n€IN ; I[sub]n[/sub]*I[sub]n+1[/sub]=[tex]\frac{\pi}{2(n+1)(n+2)(n+3)}[/tex]
b) prouver que lim(n[tex]\sqrt{n}I_n[/tex])=[tex]\sqrt{\frac{\pi}{2}}[/tex]
5) Montrer que [tex]I_{2n}=\frac{(2n)! \pi}{2^{2n+2}n ! (n+1)! }[/tex] et en déduire l'expression de I[sub]2n+1[/sub]
Pouvez vous me donner des indices pour ses questions ?
Re: Intégrales suites
Bonjour
On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] =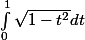 et I[sub]n[/sub]=
et I[sub]n[/sub]=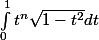 pour tout n€IN
pour tout n€IN
1)on pose f(x)=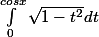 pour tout x€IR
pour tout x€IR
a)Montrer que f est derivable sur IR puis calculer f'(x)
b) Déterminer f(x) pour x€[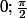 ] puis en déduire la valeur de I[sub]0[/sub]
] puis en déduire la valeur de I[sub]0[/sub]
c) Interpréter graphiquement l'integrale I[sub]0[/sub] et retrouver sa valeur
2)a) Montrer que la suite (I[sub]n[/sub])est décroissante et minoré. Que peut-on en deduire ?
b) Montrons que pour tout n€IN ; 0<=I[sub]n[/sub]<=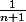 puis en déduire lim(I[sub]n[/sub]) en +oo
puis en déduire lim(I[sub]n[/sub]) en +oo
3)a) calculer I[sub]1[/sub]
b) À l'aide d'une intégration par parties , montrer que pour tout n€IN ; I[sub]n+2[/sub]=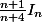 .
.
c) Montrer que pour tout n€IN ;
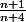 <=
<=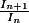 <=1 puis calculer lim(
<=1 puis calculer lim(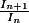 ) en +oo
) en +oo
4)a)Montrer par récurrence que pour tout n€IN ; I[sub]n[/sub]*I[sub]n+1[/sub]=(n+2)(n+3)})
b) prouver que lim(n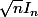 )=
)=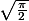
5) Montrer que! \pi}{2^{2n+2}n ! (n+1)! }) et en déduire l'expression de I[sub]2n+1[/sub]
et en déduire l'expression de I[sub]2n+1[/sub]
Pouvez vous me donner des indices pour ses questions ?
On définit la suite (I[sub]n[/sub]) par I[sub]0[/sub] =
1)on pose f(x)=
a)Montrer que f est derivable sur IR puis calculer f'(x)
b) Déterminer f(x) pour x€[
c) Interpréter graphiquement l'integrale I[sub]0[/sub] et retrouver sa valeur
2)a) Montrer que la suite (I[sub]n[/sub])est décroissante et minoré. Que peut-on en deduire ?
b) Montrons que pour tout n€IN ; 0<=I[sub]n[/sub]<=
3)a) calculer I[sub]1[/sub]
b) À l'aide d'une intégration par parties , montrer que pour tout n€IN ; I[sub]n+2[/sub]=
c) Montrer que pour tout n€IN ;
4)a)Montrer par récurrence que pour tout n€IN ; I[sub]n[/sub]*I[sub]n+1[/sub]=
b) prouver que lim(n
5) Montrer que
Pouvez vous me donner des indices pour ses questions ?
Re: Intégrales suites
Bonjour
Pour le 1. La fonction=\sqrt{1-t^2}) est continue sur [-1,1] donc admet une primitive notée H définie sur [-1,1]. On peut calculer F mais je n'ai pas encore lu le sujet entier alors on peut attendre pour l'instant.
est continue sur [-1,1] donc admet une primitive notée H définie sur [-1,1]. On peut calculer F mais je n'ai pas encore lu le sujet entier alors on peut attendre pour l'instant.
Ecrire alors f(x) avec la fonction H....
pour le 1b, 1 c l'indication suffit.
Pour le 1. La fonction
Ecrire alors f(x) avec la fonction H....
pour le 1b, 1 c l'indication suffit.
Re: Intégrales suites
Helenedupain a écrit:J'ai pas du tout compris
Alors voila en détail
On pose
Alors par définition f(x)=H(cos(x))-H(0)=H(cos(x)) qui une fonction bien définie sur
D'autre part f est dérivable sur R (composée de fonction dérivables) et de plus f'(x)=-sin(x)H'(cos(x))=-sin(x)h(cos(x))=.....
remplacer h par son expression, simplifier puis continuer....
Re: Intégrales suites
Non, il y 2 erreurs ds ce que tu écris:
d'abord=g(cos(x))-g(cos(0))=g(cos(x))-g(1))
Puis=-sin(x) g'(cos(x))=-sin(x)( \sqrt{1- cos^2(x)} )) (ce que j'ai déjà donné par ailleurs)
(ce que j'ai déjà donné par ailleurs)
d'abord
Puis
Re: Intégrales suites
f(x)=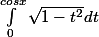 si g est la primitive de f
si g est la primitive de f
J'ai écris que=[g(x)]^{cosx}_0= g(0)-g(cosx))
Mais vous vous avez dit que f(x)=g(cosx)-g(cos0) vous avez fait comment
J'ai écris que
Mais vous vous avez dit que f(x)=g(cosx)-g(cos0) vous avez fait comment
Re: Intégrales suites
Ok je me suis trompé pour cette cste (je n'ai pas le sujet sous les yeux quand j'écris)
C'est bien g(0) mais de toute façon ensuite ça devient bon puisque g(0) est une constante qui disparait quand on dérive.
C'est bien g(0) mais de toute façon ensuite ça devient bon puisque g(0) est une constante qui disparait quand on dérive.
Re: Intégrales suites
Donc c'est vrai ce que j'avais fait f'(x) =g'(cosx) =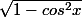
Ou bien j'ai oublié un truc ?
Ou bien j'ai oublié un truc ?
Re: Intégrales suites
Soit g la primitive de 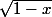
f(x)=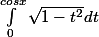 si g est la primitive de f
si g est la primitive de f
=[g(x)]^{cosx}_0= g(cosx)-g(0))
f'(x) =g'(cosx)-g'(0)=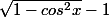
C'est correct la ?
f(x)=
f'(x) =g'(cosx)-g'(0)=
C'est correct la ?
Re: Intégrales suites
Bonjour
L'expression de f est correcte mais pas l'expression de g. Est-ce une faute de frappe?
De toute façon as-tu le niveau de base pour faire cet exercice?
En effet connais-tu l'expression de la dérivée de u(v(x))? (en admettant que u et v sont dérivables)
L'expression de f est correcte mais pas l'expression de g. Est-ce une faute de frappe?
De toute façon as-tu le niveau de base pour faire cet exercice?
En effet connais-tu l'expression de la dérivée de u(v(x))? (en admettant que u et v sont dérivables)
Re: Intégrales suites
J'ai pas mal de choses à votre absence
1a)
Soit g [rouge]une[/rouge] primitive de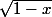
=[g(x)]^{cosx}_0= g(cosx)-g(0))
f'(x)=(g(cosx))'-(g(0))'= =-sinx|sinx|
=-sinx|sinx|
b)=\dfrac{1}{4}sin2x-\dfrac{x}{2}+c)
Or f(π/2)=0
=>=\dfrac{1}{4}sin2x-\dfrac{x}{2}+\dfrac{\pi}{4})
=\dfrac{\pi}{4})
C) l'intégral I[SUB]0[/SUB] est l'aire du quart du cercle de rayon 1 or l'air d'un quart de cercle égal π*r[SUP]2[/SUP]/4
Donc I[SUB]0[/SUB]=π/4
2)a)I[sub]n+1[/sub]-I[sub]n[/sub]=)
Sur [0; 1] donc I[sub]n+1[/sub]-I[sub]n[/sub]<=0 donc la (I[sub]n[/sub]) est décroissante
donc I[sub]n+1[/sub]-I[sub]n[/sub]<=0 donc la (I[sub]n[/sub]) est décroissante
1a)
Soit g [rouge]une[/rouge] primitive de
f'(x)=(g(cosx))'-(g(0))'=
b)
Or f(π/2)=0
=>
C) l'intégral I[SUB]0[/SUB] est l'aire du quart du cercle de rayon 1 or l'air d'un quart de cercle égal π*r[SUP]2[/SUP]/4
Donc I[SUB]0[/SUB]=π/4
2)a)I[sub]n+1[/sub]-I[sub]n[/sub]=
Sur [0; 1]
Re: Intégrales suites
Donc Pour démontré que la suite (In) est minoré je peux procédé de la même façon
J'ai sur [0; 1]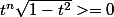 (1) et
(1) et 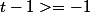 (2)
(2)
En faisant le produit (1)et(2) on à>=0)
Donc la suite In est minoré par 0
J'ai sur [0; 1]
En faisant le produit (1)et(2) on à
Donc la suite In est minoré par 0
Re: Intégrales suites
Pour la question 2.b
J'essaie de démontrer l'inégalité mais j'arrive pas
√2<= <=0
<=0
0<=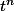 <=1
<=1
En faisant le produit je ne trouve pas les inégalités à démontré
J'essaie de démontrer l'inégalité mais j'arrive pas
√2<=
0<=
En faisant le produit je ne trouve pas les inégalités à démontré
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 101 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
