Integration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nemid
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Mai 2017, 22:02
-
 par nemid » 17 Juin 2017, 08:22
par nemid » 17 Juin 2017, 08:22
bonjour

:
je voudais savoir comment montrer que cette fonction est integrable (pour la mesure de Lebesgue sur
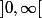
}{u^2}du)
je sais que l'equivalence en 0 c'est 1/2 mais ...
mercii




-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 17 Juin 2017, 10:28
par capitaine nuggets » 17 Juin 2017, 10:28
Salut !
Les problèmes se situent en

et en

.
Montre que la fonction
}{u^2})
est prolongeable par continuité en

.
Pour

, utilise le fait que
 \le 2)
et majore
}{u^2} {\rm d} u)
par une intégrale
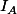
telle que lorsque
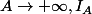
converge. Tu auras alors la convergence de
}{u^2} {\rm d} u)
-
nemid
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Mai 2017, 22:02
-
 par nemid » 17 Juin 2017, 12:13
par nemid » 17 Juin 2017, 12:13
capitaine nuggets a écrit:Salut !
Les problèmes se situent en

et en

.
Montre que la fonction
}{u^2})
est prolongeable par continuité en

.
Pour

, utilise le fait que
 \le 2)
et majore
}{u^2} {\rm d} u)
par une intégrale
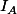
telle que lorsque
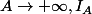
converge. Tu auras alors la convergence de
}{u^2} {\rm d} u)
merci beaucoupp





-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 17 Juin 2017, 17:34
par Lostounet » 17 Juin 2017, 17:34
On va pas calculer l'intégrale? :p C'est plus amusant !
Elle vaut pi/2 par le théorème des résidus.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
nemid
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Mai 2017, 22:02
-
 par nemid » 17 Juin 2017, 23:26
par nemid » 17 Juin 2017, 23:26

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Juin 2017, 09:21
par capitaine nuggets » 18 Juin 2017, 09:21
Sinon, on peut s'en sortir sans analyse complexe en faisant intervenir une intégrale double, en utilisant Fubini et en connaissant le résultat de l'intégrale de Dirichlet. En remarquant que
}{u} = \int_0^1 \sin(ux)\ {\rm d} x)
, on a :
}{u^2}\ {\rm d} u = \int_0^{+\infty} \left( \int_0^1 \frac{\sin(ux)}{u}\ {\rm d} x \right) {\rm d} u)
.
Par le théorème de Fubini, en intervertissant les intégrales et en connaissant la valeur de l'intégrale de Dirichlet
}{t}\ {\rm d}t=\frac \pi 2)
, on en déduit que le résultat annoncé par
Lostounet.
Lostounet a écrit:On va pas calculer l'intégrale? :p C'est plus amusant !
Elle vaut pi/2 par le théorème des résidus.
Quel contour prendrais-tu ?
-
nemid
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Mai 2017, 22:02
-
 par nemid » 18 Juin 2017, 12:44
par nemid » 18 Juin 2017, 12:44
merciiii


-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 18 Juin 2017, 17:39
par Pythales » 18 Juin 2017, 17:39
Sans utiliser Fubini ni les résidus, une simple intégration par parties montre que l'intégrale est égale à
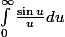
Sinon par les résidus, considérer
=\frac{1-e^{iz}}{z^2})
que l'on intègre sur le contour 0,infini, puis sur le demi cercle de rayon infini, puis sur -infini,0 et enfin sur le demi cercle de centre O dont le rayon tend vers 0
Quant à
^n})
elle s'intégre aussi par les résidus. Le résidu correspondant à
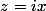
est un peu "complexe" à calculer, mais on trouve
...(2n-2)\pi}{(n-1)!2^{2n-1}x^{2n-1}})

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Juin 2017, 18:21
par capitaine nuggets » 18 Juin 2017, 18:21
Pythales a écrit:Sans utiliser Fubini ni les résidus, une simple intégration par parties montre que l'intégrale est égale à
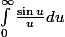
Ouais, c'est pas faux !
Pythales a écrit:Sinon par les résidus, considérer
=\frac{1-e^{iz}}{z^2})
que l'on intègre sur le contour 0,infini, puis sur le demi cercle de rayon infini, puis sur -infini,0 et enfin sur le demi cercle de centre O dont le rayon tend vers 0
Pourquoi considères-tu cette fonction et ce contour ? Pourquoi ne pourrais-t-on pas considérer le même contour mais sans le demi cercle de centre O dont le rayon tend vers 0 ? A savoir :

,

, puis sur le demi cercle de rayon infini, puis sur

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
 :
: :
:et en
.
est prolongeable par continuité en
.
, utilise le fait que
et majore
par une intégrale
telle que lorsque
converge. Tu auras alors la convergence de








que l'on intègre sur le contour 0,infini, puis sur le demi cercle de rayon infini, puis sur -infini,0 et enfin sur le demi cercle de centre O dont le rayon tend vers 0