Et tu prétends avoir compris la preuve qui utilise Krein-Milman ?
Si c'était le cas, tu ne poserais pas cette question.
Convexité et Compacité
26 messages
- Page 2 sur 2 - 1, 2
Re: Convexité et Compacité
Salam,
revoyons la preuve:
1) et
et  sont compacts
sont compacts 
 et
et 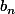 sont atteints comme max.
sont atteints comme max. 
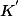 et
et 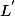 non vides.
non vides.
2)Si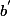 n'est pas extremal dans
n'est pas extremal dans 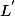 alors
alors 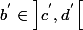 avec
avec 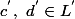 . Il suffit de remonter à
. Il suffit de remonter à  en portant avec nous
en portant avec nous 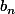 pour voir que
pour voir que  ne serait pas extremal dans
ne serait pas extremal dans  !
!
3)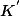 et
et 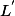 sont bornés car
sont bornés car  et
et  le sont.
le sont.
4) Si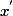 et
et 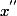 dans
dans 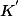 alors
alors ,\ (x^{''},a_{n})\in K)
x^{''},a_{n}) \in K) pour tout
pour tout 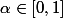 ( n'oublions pas que
( n'oublions pas que  est convexe)
est convexe) 
x^{''})
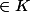 (conclure).
(conclure).
Si) une suite dans
une suite dans 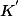 tq
tq 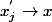 , alors
, alors \rightarrow (x,a_{n})\in K) (tu sais pourquoi).
(tu sais pourquoi).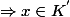 (conclure).
(conclure).
De même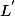 est convexe compact.
est convexe compact.
5) Nous arrivons à la pièce maîtresse de la preuve:
Hyp .Rec assure l'existence de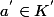 tq
tq 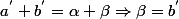 .
.
prenons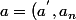) et on aura sans souffrance
et on aura sans souffrance 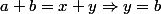 (implication de départ pour
(implication de départ pour  )
)
bien entendu, en utilisant dans la propriété, élémentaire mais efficace(ici!), suivante
la propriété, élémentaire mais efficace(ici!), suivante
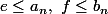 avec
avec 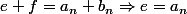 et
et 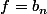 .
.
Je reconnais que c'est une très belle preuve.
Si j'ai un problème, je n'aurai aucun complexe pour demander de l'aide! La preuve est que je suis das ce forum.
Mais mon objectif est de trouver des preuves élémentaires; je l'ai déjà dit, pour les adapter à un niveau plus bas. Alors, si tu préfères les choses avancées, j'ai posté une autre question qui traite le module d'un compact d'opérateurs. (c'est bien sûr une motivation)
Cordialement.
revoyons la preuve:
1)
2)Si
3)
4) Si
Si
De même
5) Nous arrivons à la pièce maîtresse de la preuve:
Hyp .Rec assure l'existence de
prenons
bien entendu, en utilisant dans
Je reconnais que c'est une très belle preuve.
Si j'ai un problème, je n'aurai aucun complexe pour demander de l'aide! La preuve est que je suis das ce forum.
Mais mon objectif est de trouver des preuves élémentaires; je l'ai déjà dit, pour les adapter à un niveau plus bas. Alors, si tu préfères les choses avancées, j'ai posté une autre question qui traite le module d'un compact d'opérateurs. (c'est bien sûr une motivation)
Cordialement.
Re: Convexité et Compacité
Bon, j'espère que tu ne vas plus demander une nouvelle fois une preuve de
La preuve qu'on a utilise Krein-Milman. On peut trouver ça regrettable, mais tu n'as pas donné de preuve sans Krein-Milman ; alors à quoi sert de répéter que tu préfères les preuves élémentaires ? Par ailleurs, Krein-Milman, il n'y a vraiment pas de quoi s'en faire une montagne.
bagabd a écrit:trois compacts convexes et
convexe
avec
et
.
A-t-onet
?
La preuve qu'on a utilise Krein-Milman. On peut trouver ça regrettable, mais tu n'as pas donné de preuve sans Krein-Milman ; alors à quoi sert de répéter que tu préfères les preuves élémentaires ? Par ailleurs, Krein-Milman, il n'y a vraiment pas de quoi s'en faire une montagne.
Re: Convexité et Compacité
Salam,
d'accord! Faisons un effort pour résoudre la question "module d'un compact d'opérateurs".
J'ai oublié, qu'est ce que tu entends plus exactement par un changement linéaire pour avoir) ? Une rotation non?
? Une rotation non?
Cordialement.
d'accord! Faisons un effort pour résoudre la question "module d'un compact d'opérateurs".
J'ai oublié, qu'est ce que tu entends plus exactement par un changement linéaire pour avoir
Cordialement.
Modifié en dernier par bagabd le 11 Juil 2016, 15:41, modifié 2 fois.
Re: Convexité et Compacité
Non, pas forcément une rotation. Juste un changement linéaire de coordonnées, ça a un sens bien clair, non ?
Je te laisse faire toi-même l'effort sur ton autre question, je n'ai pas envie de m'y intéresser - désolé.
Je te laisse faire toi-même l'effort sur ton autre question, je n'ai pas envie de m'y intéresser - désolé.
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
