Espace de Hilbert (complétude - densité - compacité)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 08 Nov 2009, 15:10
par MacManus » 08 Nov 2009, 15:10
Bonjour
MacManus a écrit:On considère l'espace de Hilbert
=\{(a_n)_{n \ge 0}\in \mathbb{C^N} / \bigsum_{n=0}^{+\infty}|a_n|^2 =\bigsum_{n=0}^{+\infty}a_n \bar{b_n})
Soit
=\{a \in l^2(\mathbb{N}) / \bigsum_{n=0}^{+\infty}n^2|a_n|^2 _{h^1(\mathbb{N})}=\bigsum_{n=0}^{+\infty}(1+n^2)a_n \bar{b_n})
1/ Montrer que
})
est un
produit scalaire, et que
)
muni de ce produit scalaire est un
espace de Hilbert. (Hilbert = préhilbertien + complet)
2/ Montrer que
)
est
dense dans
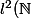) 1/
1/ --> J'ai montré que
})
est bien un produit scalaire.
Pour montrer que l'on a un espace de Hilbert, il ne reste plus qu'a montrer que toute suite de Cauchy de cet espace est convergente dans cet espace. Sinon on peut montrer que toute série normalement convergente est convergente (tjrs dans cet espace). J'ai opté pour la 1ère méthode. On sait que
)
est un espace vectoriel normé, où
}=\sqrt{_{h^1(\mathbb{N})})
Soit
_n)
une suite de Cauchy de
)
, on a :
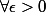
,
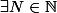
,
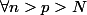
,
}^2 0)
,
)
,
)
telle que
}< \epsilon)
Est-ce que cette définition de la densité est correcte ? Comment puis-je le montrer ?...
Merci beaucoup pour vos réponses !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Nov 2009, 19:21
par Doraki » 08 Nov 2009, 19:21
MacManus a écrit:J'ai opté pour la 1ère méthode. On sait que
)
est un espace vectoriel normé, où
}=\sqrt{_{h^1(\mathbb{N})})
Soit
_n)
une suite de Cauchy de
)
, on a :
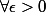
,
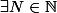
,
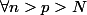
,
}^2 < \epsilon^2)
cad : avec les mêmes conditions,
|a_{n+p}-a_n|^2 < \epsilon^2}) (*)
(*). Or, on sait que
_n \subset h^1(\mathbb{N}))
implique que
_n \subset l^2(\mathbb{N}))
, d'après la définition de
)
. Puisque
)
est complet (pour la norme associée), on en déduit que la suite
_n)
admet une limite dans
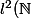)
, que je note a.
Attention, quand tu inclues h1 dans l2, la norme utilisée change donc les notions de suites de Cauchy, de convergence et de complétude ne sont pas équivalentes.
Pour commencer à combler ces trous il faudrait par exemple dire pourquoi une suite de Cauchy dans h1 est une suite de Cauchy dans l2
Sinon pour le 2, tu as une bonne traduction mais on en est pas là.
 par alavacommejetepousse » 08 Nov 2009, 19:26
par alavacommejetepousse » 08 Nov 2009, 19:26
bonsoir
je comprends rien
les éléments sont des suites
pour prendre une suite de cauchy il faut une suite de suites
ta notation avec un seul indice n en rend pas compte
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Nov 2009, 19:32
par Doraki » 08 Nov 2009, 19:32
C'est vrai, l'encadré avec l'astérisque verte est totalement nonsensique.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 08 Nov 2009, 19:52
par MacManus » 08 Nov 2009, 19:52
Bonsoir et merci
Oui, je suis d'accord, il faut considérer une suite de suites!
On sait que
 \subset l^2(\mathbb{N}))
. On va donc considérer la norme associée à
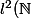)
.
Mais je ne vois pas comment montrer que toute suite de Cauchy de
)
est une suite de Cauchy de
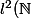)
...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 08 Nov 2009, 20:14
par MacManus » 08 Nov 2009, 20:14
En gros, on sait que toute suite de
)
est une suite de
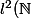)
. Je dois montrer que toute suite de Cauchy de
)
est une suite de Cauchy de
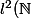)
, qui convergera donc dans
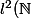)
, donc dans
)
, pour la norme associée à
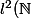)
. J'aurai montré ainsi que
)
est complet, c'est bien ça ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 08 Nov 2009, 20:45
par kazeriahm » 08 Nov 2009, 20:45
bah précisément tu montres que Cauchy dans h¹ => Cauchy dans l², donc convergeant
faut que tu montres que la limite alors obtenu est dans h¹ pour montrer qu'il est complet
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Nov 2009, 20:49
par Doraki » 08 Nov 2009, 20:49
Et savoir que u_n converge vers u pour la norme de l2, même si les u_n et u sont dans h1, ça ne veut pas non plus dire qu'il y a convergence pour la norme de h1.
Le mieux ce serait presque que tu oublies que l'espace l2 existe et que tu montres que h1 est complet sans faire n'importe quoi avec une norme de l2 qui n'a rien à voir.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 09 Nov 2009, 07:38
par kazeriahm » 09 Nov 2009, 07:38
La norme h¹ a beaucoup à voir avec la norme l² !
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 09 Nov 2009, 20:09
par MacManus » 09 Nov 2009, 20:09
Bonsoir à tous!
Je peine à montrer le résultat. Je montre qd même ce que j'ai fait.
On sait que
\subset l^2(\mathbb{N}))
Soit
_k)
une suite de Cauchy d'éléments de
)
(une suite de suites).
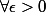
,
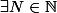
,
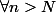
,
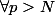
,
}^2 \le \epsilon^2)
cad :
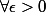
,
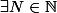
,],
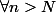
,
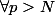
,
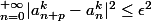
or
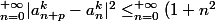|a_{n+p}^{k}-a_{n}^{k}|^2 \le \epsilon^2)
Donc, toute suite de Cauchy de
)
est une suite de Cauchy de
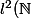)
. Puisque
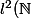)
est complet, on a que
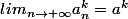
dans
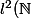)
. De plus, en faisant
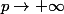
dans la double inégalité, on a que :
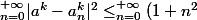|a^{k}-a_{n}^{k}|^2 \le \epsilon^2)
. De plus la seconde inégalité signifie que
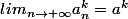
dans
)
. D'où la complétude.
Mais je ne tiens pas compte de ce que dit Doraki dans son dernier post et ça m'embête et j'ai aussi l'impression de tout mélanger ! Bref si vous avez le temps de me corriger ! Merci beaucoup en tout cas!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Nov 2009, 20:42
par Doraki » 09 Nov 2009, 20:42
Alors déjà l'indice dans les sommes c'est k (et puis p>n c'est farfelu)
Ensuite je ne suis absolument pas convaincu de la manière dont tu fais tendre p vers l'infini pour chacun des termes de la série infinie.
C'est pas parceque séparément, chaque a_n^k tend vers a^k quand n tend vers l'infini que tu peux en déduire quelquechose sur un truc qui parle de tous les a_n^k en même temps.
La suite de suites
(1, 0, 0....)
(1, 1/2, 0, 0...)
(1, 1/2, 1/3, 0, 0...)
....
tend vers la suite (1/k) dans l2, c'était au départ des suites de h1, mais la limite n'est même pas dans h1.
(Bien sur, ce n'était pas une suite de cauchy dans h1, mais c'est pour illustrer comment on s'en fiche totalement de savoir que (un) -> u dans l2)
Une piste serait de trouver un homéomorphisme entre h1 et l2 (une isométrie, même)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 09 Nov 2009, 21:10
par MacManus » 09 Nov 2009, 21:10
Doraki a écrit:Alors déjà l'indice dans les sommes c'est k (et puis p>n c'est farfelu)
Oui on considère que c'est k qui tend vers l'infini, donc on somme sur k. Et j'aurais dû dire pour tout n>N et tout p>N.
Doraki a écrit:Ensuite je ne suis absolument pas convaincu de la manière dont tu fais tendre p vers l'infini pour chacun des termes de la série infinie.
C'est pas parceque séparément, chaque a_n^k tend vers a^k quand n tend vers l'infini que tu peux en déduire quelquechose sur un truc qui parle de tous les a_n^k en même temps.
La suite de suites
(1, 0, 0....)
(1, 1/2, 0, 0...)
(1, 1/2, 1/3, 0, 0...)
....
tend vers la suite (1/k) dans l2, c'était au départ des suites de h1, mais la limite n'est même pas dans h1.
(Bien sur, ce n'était pas une suite de cauchy dans h1, mais c'est pour illustrer comment on s'en fiche totalement de savoir que (un) -> u dans l2)
Je ne vois pas bien comment tu utilises h1 et l2 avec cet exemple...
Je suis d'accord pour dire que cette suite de suites que tu donnes tend vers la suite (1/k), mais pourquoi dans l2 ? pourquoi des suites de h1 au départ ?
J'suis un peu pommé dsl, en plus fatigué !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 09 Nov 2009, 21:34
par kazeriahm » 09 Nov 2009, 21:34
Je suis pas d'accord avec toi Doraki. Si (u_n) est une suite de Cauchy de h¹, elle admet une limite u dans l², et il faut montrer que ce u est dans h¹.
Je note T le cercle unité. l² est l'espace des coefficients de Fourier des fonctions L²(T). h¹ est l'espace des coefficients de Fourier des fonctions L²(T), dont la dérivée (au sens des distributions) est encore dans L²(T). Une méthode consiste à utiliser la continuité de l'opérateur dérivation, et pour ca on utilise le fait que la limite u est dans l². Mais il y a surement moyen de le faire plus simplement avec du travail avec les suites.
 par alavacommejetepousse » 10 Nov 2009, 07:48
par alavacommejetepousse » 10 Nov 2009, 07:48
bonjour
je nai pas tout lu (je redis sans doute des choses dites)
1 on sait que ( l2 ,ll ll2 ) est complet (oui?)
2 h1 est inclus dans l2 et la norme sur h1 est supérieure à la norme del2
3 on en déduit qu'une suite decauchy dans h1 l'est aussi dans l2
4 d'où cette suite converge vers un élément de l2 pour ll ll2
5 reste à montrer que la convergence à lieu au sens de h1
ce qui est facile il suffit de réecrire (correctement) la déf d'une suite de cauchy de tronquer la série à 1 rang arbitraire Q , de passer à la limite (sur n) (terme à terme) et de repasser à la limite sur Q
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 10 Nov 2009, 08:37
par kazeriahm » 10 Nov 2009, 08:37
Ouaip, c'est plus ou moins ce qu'a fait MacManus il me semble.
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 10 Nov 2009, 11:47
par MacManus » 10 Nov 2009, 11:47
alavacommejetepousse a écrit:bonjour
je nai pas tout lu (je redis sans doute des choses dites)
1 on sait que ( l2 ,ll ll2 ) est complet (oui?)
2 h1 est inclus dans l2 et la norme sur h1 est supérieure à la norme del2
3 on en déduit qu'une suite decauchy dans h1 l'est aussi dans l2
4 d'où cette suite converge vers un élément de l2 pour ll ll2
Bonjour. Effectivement je pense l'avoir montré dans mon post de 20h09, mis à part le fait que l'on somme bien sur k.
5 reste à montrer que la convergence à lieu au sens de h1
ce qui est facile il suffit de réecrire (correctement) la déf d'une suite de cauchy de tronquer la série à 1 rang arbitraire Q , de passer à la limite (sur n) (terme à terme) et de repasser à la limite sur Q
C'est là où je piétine...mais je vais y réfléchir
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 10 Nov 2009, 17:26
par MacManus » 10 Nov 2009, 17:26
Bonsoir
Je suis presqu'au bout (du rouleau :doute2: ) j'ai réécris la définition pour une suite d'être de Cauchy dans h1 (avec la norme associée à h1 donc), je tronque, mais en passant à la limite en n terme à terme, je ne vois pas trop ce que ça change... je comprends pas pk je ne m'en sors pas
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Nov 2009, 17:33
par Doraki » 10 Nov 2009, 17:33
Montre ce que tu fais pour voir si ça peut aboutir.
Essaye de prendre la preuve de la complétude de l2 comme modèle voir comment ça fonctionne.
Sinon, je te rebalance "trouve une isométrie entre h1 et l2".
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 11 Nov 2009, 11:15
par MacManus » 11 Nov 2009, 11:15
Bonjour !
Je m'accroche

On sait que
\subset l^2(\mathbb{N}))
: toute suite de
)
est une suite de
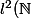)
. Considérons une suite de Cauchy
_{n \in \mathbb{N}})
de
)
(suite de suites). On a :
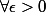
,
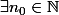
,
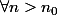
,
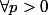
,
})
0[/tex],
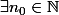
,
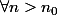
,
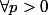
,
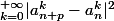

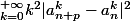
0[/tex],
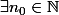
,
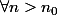
,
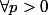
,
})
0[/tex],
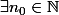
,
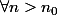
,
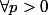
,
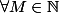
, on a
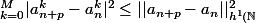
<
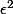
En faisant
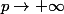
, on obtient
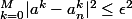
, ce qui implique
)


Ce qui prouverait la complétude... mais je ne suis pas sûr de moi
Merci pour votre aide une fois de plus
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
