Fonction croissante

[ARIMA]

Bonjour,
un fil que j'ai vu récemment sur le forum m'a inspiré cette question.

Que dire de l'ensemble des points de discontinuité d'une fonction croissante (ou monotone évidemment)?

[Trident]

Exercice classique. L'ensemble est dénombrable (ou fini). Notons cet ensemble D.

Il existe pleins de façons de démontrer ceci mais une qui m'avait plu consistait à montrer que D et Q étaient en injection.

Il faut savoir qu'une fonction monotone f admet en tout point a une limite à gauche notée f(a-) et une limite à droite notée f(a+). Donc dire que f est discontinue en a signifie que f(a-) != f(a+). En supposant f croissante par exemple, on a f(a-) < f(a+).

Considérons la fonction g : D -> Q qui à x dans D associe un rationnel se situant dans l'intervalle [f(x-);f(x+)]. On se débrouille (dans le choix du rationnel, il y en a une infinité car Q est dense dans R)pour faire en sorte que g soit injective et on prouve que D est dénombrable car Q l'est.

Bon, c'est assez vite expliqué mais tu trouves une démo rapidement sur internet.

[Trident]

Exercice classique. L'ensemble est dénombrable (ou fini). Notons cet ensemble D.

Il existe pleins de façons de démontrer ceci mais une qui m'avait plu consistait à montrer que D et Q étaient en injection.

Il faut savoir qu'une fonction monotone f admet en tout point a une limite à gauche notée f(a-) et une limite à droite notée f(a+). Donc dire que f est discontinue en a signifie que f(a-) != f(a+). En supposant f croissante par exemple, on a f(a-) < f(a+).

Considérons la fonction g : D -> Q qui à x dans D associe un rationnel se situant dans l'intervalle [f(x-);f(x+)]. On se débrouille (dans le choix du rationnel, il y en a une infinité car Q est dense dans R)pour faire en sorte que g soit injective et on prouve que D est dénombrable car Q l'est.

Bon, c'est assez vite expliqué mais tu trouves une démo rapidement sur internet.

[Ben314]

Salut,
Juste une remarque : tu n'as pas "à te débrouiller" pour que ta fonction soit injective, mais tu as à démontrer que la croissance de la fonction entraine que, quelque soit les choix des différents rationnel dans les intervalles, ta fonction est injective.

Perso, je préfère la preuve plus "visuelle" (et n'utilisant pas l'axiome du choix) consistant à montrer que, pour tout segment et toute partie finie de on a
Cela prouve que, pour tout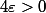 , l'ensemble est fini (de cardinal ) et on conclue en utilisant le fait que est réunion dénombrable d'ensembles finis.

Sinon, s'il y en a que ça amuse, QUESTION : D peut-il être dense dans ?

[Trident]

En effet Ben, le choix de n'importe quel rationnel rend la fonction injective.

En revanche, il ne me semble pas nécessaire d'avoir recours à l'axiome du choix pour le choix d'un rationnel dans ]f(x-);f(x+)[, dis moi si je me trompe.
Si je considère l'ensemble des rationnels dedans ]f(x-);f(x+)[ écrits sous forme irréductible et je sélectionne ceux s'écrivant avec le plus petit dénominateur (l'ensemble des dénominateurs est alors une partie de N non vide donc admet un plus petit élément) puis parmi ceux qui me restent, je prend celui ayant le plus petit nominateur (l'ensemble des nominateurs est alors une partie de N non vide donc admet un plus petit élément). Dans ce cas, je n'ai pas recours à l'axiome du choix non?

Pour ta question, la réponse est oui mais je l'avais lu dans un cours AGREG Maths. La fonction en question était bizarre sous forme de somme (je ne donne pas la réponse pour celui qui veux chercher), je suis curieux de savoir ta démarche pour y penser. Quand j'y avais réfléchi, j'avais essayé de une fonction f de sorte que D soit un sous groupe de R+. Quand x et y sont dans D, j'aimerais bien que x+y soit dans D, i.e f( (x+y)+) != f( (x+y)-) tout en utilisant f(x+) != f(x-) , f(y+) != f(y-). Je n'avais rien trouvé d'intéressant. Et puis montrer que si x est dans D, -x est dans D. Une fonction paire marcherait mais c'est pas monotone ! Bref, cette piste ne semble mener à rien.