Si
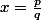
(irréductible) est un rationnel alors
=\frac{1}{p+q})
.
Or il existe une suite
_{n\geq 0})
de non rationnels qui tend vers x et comme
=0)
pour tout n, on a
=0\not=f(x))
ce qui montre que f n'est pas continue en x.
Si x n'est pas un rationnel, fixons un

.
L'intervalle [x-1,x+1] ne contient qu'un nombre fini de rationnels
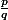
tels que
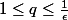
(pour q fixé, un intervalle de largeur 2 contient au plus 2q+1 rationnels p/q) et aucun d'entre eux n'est égal à x (car x irrationnel).
Cela permet de voir qu'il existe un petit intervalle ouvert I contenant x et aucun rationnel
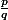
tel que
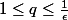
. Pour tout y dans I, on a alors :
Soit y est irrationnel et f(y)=0.
Soit y=p/q (irréductible) est rationnel et, par construction de I, on a
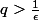
donc
=\frac{1}{p+q}\leq\frac{1}{q}<\varepsilon)
Conclusion : pour tout y dans I, on a
-f(x)|=|f(y)-0|<\epsilon)
ce qui prouve la continuité de f en x.
qui prend la valeur
en tout rationnel ayant pour représentation irréductible
et nulle ailleurs.
