Espaces vectoriels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 07 Fév 2014, 22:31
par LauraR » 07 Fév 2014, 22:31
Bonsoir
Mon exercice consiste à mettre sous forme Vect les solutions de y'+ay=0
Je connais les solutions de cette équation différentielle qui est y=kexp(-ax) mais je ne vois pas comment je peux l'écrire
Quelqu'un pourrait m'aider s'il vous plaît ?
Je remercie d'avance ceux qui m'aideront à résoudre cette exercice
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 08 Fév 2014, 00:28
par DamX » 08 Fév 2014, 00:28
LauraR a écrit:Bonsoir
Mon exercice consiste à mettre sous forme Vect les solutions de y'+ay=0
Je connais les solutions de cette équation différentielle qui est y=kexp(-ax) mais je ne vois pas comment je peux l'écrire
Quelqu'un pourrait m'aider s'il vous plaît ?
Je remercie d'avance ceux qui m'aideront à résoudre cette exercice
Bonsoir,
Qu'est-ce que k dans ton résultat, que peux t-il valoir ? Parallement que désigne Vect(f) par rapport a f ?
Damien
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 08 Fév 2014, 10:58
par LauraR » 08 Fév 2014, 10:58
DamX a écrit:Bonsoir,
Qu'est-ce que k dans ton résultat, que peux t-il valoir ? Parallement que désigne Vect(f) par rapport a f ?
Damien
k représente une constante elle vaut 1 Vect(f) correspond au sous espace vectoriel de f
mais je ne vois pas comment faire apparaître le vecteur
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 08 Fév 2014, 13:06
par Sourire_banane » 08 Fév 2014, 13:06
LauraR a écrit:k représente une constante elle vaut 1 Vect(f) correspond au sous espace vectoriel de f
mais je ne vois pas comment faire apparaître le vecteur
Salut,
Des notions à revoir.
k peut valoir n'importe quoi dans ton corps d'étude c'est en ça que c'est intéressant d'exhiber l'ensemble des sol en "Vect(...)". Revois la définition de ce qu'est
l'ensemble des combinaisons linéaires d'un vecteur donné .
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 08 Fév 2014, 21:51
par mrif » 08 Fév 2014, 21:51
DamX a écrit:Bonsoir,
Qu'est-ce que k dans ton résultat, que peux t-il valoir ? Parallement que désigne Vect(f) par rapport a f ?
Damien
Si on appelle
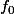
la fonction définie par
 = e^{-ax})
, l'ensemble des solutions est l'espace vectoriel de dimension 1 engendré par
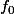
.
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 11 Fév 2014, 18:42
par LauraR » 11 Fév 2014, 18:42
Sourire_banane a écrit:Salut,
Des notions à revoir.
k peut valoir n'importe quoi dans ton corps d'étude c'est en ça que c'est intéressant d'exhiber l'ensemble des sol en "Vect(...)". Revois la définition de ce qu'est l'ensemble des combinaisons linéaires d'un vecteur donné .
ah oui :mur: c'est vrai donc on a y=kexp(a(x)) et cela correspond a toute les valeurs donc on l'écrit
Vect(kexp(a(x))) je crois ?
Juste une dernière question le k de la solution comme il vaut n'importe quelle valeur est ce qu'il faut le faire apparaître ou pas ? si non pourquoi ?
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 11 Fév 2014, 19:45
par LauraR » 11 Fév 2014, 19:45
Bonsoir
j'ai encore une question par rapport aux sous espaces vectoriels
par exemple
\in\mathbb{R}^2 / x\leq y})
n'est pas un sous espace vectoriel pourquoi ?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 11 Fév 2014, 20:11
par mrif » 11 Fév 2014, 20:11
LauraR a écrit:Bonsoir
j'ai encore une question par rapport aux sous espaces vectoriels
par exemple
\in\mathbb{R}^2 / x\leq y})
n'est pas un sous espace vectoriel pourquoi ?
Posons
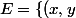\in\mathbb{R}^2 / x\leq y})
E n'est pas stable pour la multiplication par un scalaire.
.(x,y) = (-x,-y))
.
\ \in E,\ mais\ (-2,-3) \notin E\ car -2\ >\ -3)
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 11 Fév 2014, 21:33
par LauraR » 11 Fév 2014, 21:33
mrif a écrit:Posons
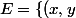\in\mathbb{R}^2 / x\leq y})
E n'est pas stable pour la multiplication par un scalaire.
.(x,y) = (-x,-y))
.
\ \in E,\ mais\ (-2,-3) \notin E\ car -2\ >\ -3)
Ok j'ai compris mais quand on a |x|=|y| est ce que c'est comme x=y ?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 11 Fév 2014, 21:53
par mrif » 11 Fév 2014, 21:53
LauraR a écrit:Ok j'ai compris mais quand on a |x|=|y| est ce que c'est comme x=y ?
|x|=|y| c'est comme (x = y ou x = -y).
Pour fixer ce genre de définition aide toi avec des exemples:
|-2| = 2 ; |2| = 2.
On a bien |-2| = |2| = 2, et 2 est différent de -2 mais on a: 2 = -(-2)
-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 11 Fév 2014, 21:55
par LauraR » 11 Fév 2014, 21:55
mrif a écrit:|x|=|y| c'est comme (x = y ou x = -y).
Pour fixer ce genre de définition aide toi avec des exemples:
|-2| = 2 ; |2| = 2.
On a bien |-2| = |2| = 2, et 2 est différent de -2 mais on a: 2 = -(-2)
Ok merci pour ton conseil j'y penserai

-
LauraR
- Membre Naturel
- Messages: 31
- Enregistré le: 07 Fév 2014, 22:24
-
 par LauraR » 11 Fév 2014, 22:15
par LauraR » 11 Fév 2014, 22:15
mrif a écrit:|x|=|y| c'est comme (x = y ou x = -y).
Pour fixer ce genre de définition aide toi avec des exemples:
|-2| = 2 ; |2| = 2.
On a bien |-2| = |2| = 2, et 2 est différent de -2 mais on a: 2 = -(-2)
Ok merci pour ton conseil je ne l'oublierai pas :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
