Topologie

[lightone]

Bonjour, je n'arrive pas à faire cette exercice, pouvez vous m'aider?

Voici l'énoncé :

Soit (oméga, d) un espace métrique.

1) Soit O, un ouvert de oméga et soit F = Oc (complémentaire de O). Montrer que pour tout x appartenant à oméga, on a l'équivalence suivante :

x appartient à O SSI il existe n appartenant à N étoile tq pour tout z appartenant à F, on a d(x,z) >= 1/n

2) Montrer que tout ouvert de oméga est réunion dénombrable de fermés.

Merci pour votre aide

[Ben314]

Salut,
- C'est quoi la contraposée de l'implication ?
- Donc la proposition en fait elle dit quoi ?
- C'est quoi la définition d'un ouvert d'un espace métrique ?

[lightone]

- d(x,z) < 1/n => z n'appartient pas à F?
- Pour moi, elle dit que si z appartient à F, z n'est pas intérieur à O et donc que la d(x, z) "sort" de O. Il n'y a donc pas de boule ouverte dans ce cas.
- un espace métrique est ouvert s'il existe r > 0 tq B(x, r) est inclus dans cet espace

[hdci]

Il faut revenir à la définition d'un ouvert : dans un espace métrique, un ouvert est une partie telle que pour tout point de la partie, il existe une boule ouverte centrée en ce point et incluse dans la partie, comme vous le rappelez.

Dit en formule :


Vous voulez montrer que


Essayez d'utiliser la première formule pour montrer la seconde. Indications :

• Si , que pouvez-vous dire de ?
• Donc que pouvez-vous dire de pour tout ?
• Enfin, une fois "connu" ce , comment choisir pour "remplacer" ce dans les formules précédentes ?

Une fois que vous aurez "vu" cela, vous pourrez vous attacher à démontrer l'équivalence formellement.

[lightone]

- Ca vaut l'ensemble vide?
- cette distance sera supérieure à epsilon
- ba il faut choisir les n qui permettent d'avoir d(x, epsilon) >= à 1/n?

[hdci]

- Ca vaut l'ensemble vide?

Oui puisque la boule est incluse dans et que est le complémentaire de

- cette distance sera supérieure à epsilon

Oui encore, puisqu'aucun élément de n'est dans la boule ils sont tous à une distance de supérieure au rayon de la boule

il faut choisir les n qui permettent d'avoir d(x, epsilon) >= à 1/n?

Plus précisément : si , que peut-on dire de pour ?

Revenons alors à l'équivalence à démontrer : comme souvent, il vaut mieux démontrer l'implication et la réciproque séparément (cela évite la plupart des erreurs de raisonnement confondant implication et équivalence).
Implication : si , alors il existe tel que parce que (... justifiez ?) et donc pour tout ... ?

Réciproque : pouvez-vous montrer que si il existe tel que , alors il existe une boule ouverte centrée en et incluse dans ?

[lightone]

Je ne vois pas trop où vous voulez en venir...

[hdci]

A quel moment décrochez-vous ?

[lightone]

si n > 1/epsilon, la boule ouverte serait toujours dans O non?

Pour l'implication, il est un n > 0 car O est ouvert mais tout z appartenant F, je ne vois pas trop ce que l'on peut dire....

[hdci]

si n > 1/epsilon, la boule ouverte serait toujours dans O non?

Exact.

Pour l'implication, il est un n > 0 car O est ouvert mais tout z appartenant F, je ne vois pas trop ce que l'on peut dire....

Il est bon ici de faire un dessin, cela aide à comprendre ce qui se passe : vous dessinez une "patate" (assez grosse), c'est . Donc , c'est tout ce qu'il y a en dehors.
Vous placez un point à l'intérieur de la patate et vous tracez un cercle centré en ce point, en disant que le rayon c'est . Le disque correspondant (c'est-à-dire dans un espace métrique la boule) est donc à l'intérieur de la patate (de ).
En ayant pris , vous allez tracer un cercle centré en et de rayon . Le nouveau disque est donc totalement inclus dans la patate.

Alors, prenez un point n'importe où dans (à l'extérieur de la patate) : est-ce que la distance entre et peut être inférieure à ? Sur le dessin cela se voit de façon évidente...

Et une fois qu'on l'a "vu", on peut le "raisonner" : comme ne peut pas être dans la boule de rayon , sa distance à est forcément plus grande que .

Le dessin permet de "comprendre ce qui se passe", le raisonnement juste après a montré que si alors il existe tel que , puis pour tout alors

Pour la réciproque c'est "presque" la même chose... Je vous laisse réfléchir un peu

[lightone]

D'accord merci, je vais réfléchir

[aviateur]

Vu la lenteur, j'expédierai bien cela de la façon suivante.
O est un ouvert, donc pour tout élément x de O il existe une boule ouverte de centre x et de rayon assez petit (prendre 1/n avec n suffisamment grand) tel que cette boule B(x,1/n) est incluse dans O. Ceci implique que tout z dans F, complémentaire de O n'est pas dans cette boule

On fait un une patate avec un x dedans, un petit rond autour de x qui reste dans la patate. On fout un z en dehors de cette patate et on voit bien que z n'est pas dans le rond. C'est pas la mer à boire.

La réciproque est du même gabarit.

[lightone]

J'avais compris le principe pour le premier sens (de gauche à droite) mais pour l'écrire correctement et mathématiquement, c'est autre chose.

[aviateur]

Ben c'est fait. Je pense qu'il ne faut pas tergiverser, c'est à dire se répéter à dire la même chose sous différentes formes.

[lightone]

Pour la question 2, auriez vous des indices à me donner svp?

[lightone]

Pour la réciproque, j'ai dit que la formule de droite était la négation d'une boule ouverte de centre x et de rayon 1/n et où z appartient à cette boule. Ce qui veut dire que cette boule ne peut pas être incluse dans F. Et puisque z appartient à F, x ne peut qu'appartenir à O.

[hdci]

Oui c'est cela : si pour tout on a alors aucun point de la boule ouverte centrée en et de rayon 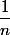n'est dans . Ils sont donc dans , et comme par hypothèse, pour tout de on trouve un entier n adéquat, cela montre que pour tout , on trouve une boule ouverte centrée en et incluse dans .

[lightone]

Merci. Et pour la question 2, vous avez des pistes à me donner?

[hdci]

Pour la question 2, je sèche... Je connais la démonstration dans le cas d'un espace vectoriel normé de dimension finie, mais elle ne s'applique pas un espace métrique quelconque.

[lightone]

Elle est peut être ressemblante non?