Topologie

[hdci]

Non, dans un evn de dimension finie, on considère des pavés donc et on démontre que dans tout intervalle ouvert est réunion dénombrable d'intervalles fermés. Donc tout pavé ouvert dans le produit cartésien est réunion dénombrable de pavés fermés, et on montre ensuite que tout ouvert est réunion dénombrable de pavés ouverts en utilisant la densité de 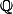dans , donc de dans

La démosntration utilise donc spécifiquement les propriétés de et des evn de dimension finie. Pas utilisable dans le cas d'un métrique quelconque.

[Ben314]

<<erreur>>

[Ben314]

(re)salut,
Pour un x de Omega donné, le fait que il existe n appartenant à N étoile tq pour tout z appartenant à F, on a d(x,z) >= 1/n, ça veut très exactement dire que x est dans la réunion des ensemble , où

Et pour ta question 2), vu le résultat du 1), tout ce que tu as à démontrer, c'est que ces ensembles sont bien tous des fermés de .
Pour se faire, il y a plusieurs solutions :
Si tu as vu la notion de fonctions continues entre espace métriques, ça peut être judicieux d'introduire la fonction et de montrer qu'elle est continue.
Sinon, tu peut soit utiliser les suites, soit montrer avec des boules que le complémentaire est ouvert.

[aviateur]

Bonsoir, serai-je mal réveillé ou plutôt déjà endormi?
En effet je vois ce raisonnement tout con pour la réciproque:
Il faut montrer que " il existe n appartenant à N étoile tq pour tout z appartenant à F, on a d(x,z) >= 1/n"
implique
Mais par hypothèse, j'en déduis que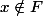 sinon on aurait . Donc

[Ben314]

Si tu parle de la question 1), y'a vraiment pas grand chose à dire : pour un donné, on a


Et si on sait pas ce que c'est que l'intérieur d'une partie d'un espace métrique, on peut aboutir au résultat sans l'avant dernière ligne en évoquant la définition d'un ouvert pour le sens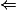 et en évoquant le fait que pour le sens .

[aviateur]

Bon d'abord j'ai pas vu la question 2) et je pensais qu'on en était encore à la question 1).
C'est pourquoi je n'ai pas regardé en détails tes réponses

Mais néanmoins pour la 1) je voyais que ça trainait trop à mon gout pour la directe et dc j'avais donné la démo. Mais la réciproque c'est pire il n'y a rien.
si pour tout z dans F et bien x n'est pas dans F. C'est tout ce que je voulais dire.

[lightone]

Je n'ai pas du tout compris ce que vous m'avez dit pour la question 2...

[aviateur]

Bonjour, tu as eu une indication alors je la reprend:
Soit les ensembles

D'après la première question ssi appartient a (au moins) un des
Ce qui veut dire que

Il faut alors démontrer que chaque est un fermé. Ce qui revient à démontrer que chaque (=complémentaire de ) est un ouvert.

Mais c'est l'ensemble des u dans tel qu'il existe 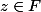vérifiant d(u,z)<1/n
Ce qui est équivalent à dire que c'est l'ensemble des u dans tel qu'il existe 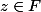avec (boule ouverte)
Ou encore cela veut dire que et c'est donc un ouvert
car toute union d'ouverts est un ouvert. cqfd