Théorème de la limite monotone
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 14:15
par mehdi-128 » 26 Aoû 2019, 14:15
Bonjour,
Soit  une fonction monotone définie sur un intervalle ouvert
une fonction monotone définie sur un intervalle ouvert 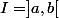 avec
avec  \in \bar \R^2) et
et 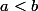 . Alors
. Alors ) et
et ) existent dans
existent dans 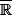
La démonstration est réalisée pour le cas

croissante et l'auteur précise : "on peut supposer sans perte de généralité que

est croissante."
Je ne comprends pas pourquoi on n'a pas besoin de refaire la démonstration pour

décroissante. Comment l'adapter rapidement pour ne pas tout refaire ?
La démonstration part du cas
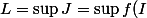)
majorée.
Soit
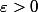
, par définition de la borne supérieure il existe un réel
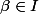
tel que
 \geq L- \varepsilon)
. D'après la croissance de

, pour
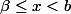
on a :
 \leq f(x) \leq L \leq L+\varepsilon)
Par définition de la limite
 = L)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Aoû 2019, 14:28
par GaBuZoMeu » 26 Aoû 2019, 14:28
Si

est décroissante, que peux-tu dire de
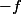
?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 14:56
par mehdi-128 » 26 Aoû 2019, 14:56
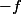
est croissante mais je ne vois pas quel point modifier dans le démonstration pour adapter.
Ça donne :
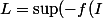 ))
majorée.
Mais c'est quoi
))
?
Puis on tombe sur pour
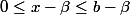
:
 \leq \varepsilon-L)
pareil ça donne rien.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Aoû 2019, 15:01
par GaBuZoMeu » 26 Aoû 2019, 15:01
Réfléchis.
Il s'agit juste d'utiliser le résultat démontré pour une fonctio croissante.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 15:14
par mehdi-128 » 26 Aoû 2019, 15:14
Intuitivement si elle est minorée elle va tendre vers la borne inférieur de
)
et si elle n'est pas minorée elle va tendre vers moins l'infini.
Donc je dois refaire toute la démonstration avec le cas
)
minoré et
)
non minoré ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Aoû 2019, 15:24
par GaBuZoMeu » 26 Aoû 2019, 15:24
Je répète: il suffit d'utiliser le résultat démontré pour une fonction croissante.
Et si

est décroissante, il y a une fonction croissante évidente à laquelle appliquer le résultat démontré !
Quel est le résultat démontré, au fait ?
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 26 Aoû 2019, 15:27
par lyceen95 » 26 Aoû 2019, 15:27
Refaire la démonstration, c'est un bien grand mot.
Recopie la démonstration, en remplaçant les mots 'croissant' par 'décroissant' , 'positif' par 'négatif' , 'plus' par 'moins' ... et voilà.
Le travail de réflexion ne devrait pas être trop compliqué.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 15:29
par mehdi-128 » 26 Aoû 2019, 15:29
Ah d'accord merci je pense avoir compris.
Supposons

décroissante.
Si
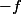
une fonction croissante définie sur
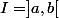
avec
 \in \bar \R^2)
et
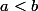
. Alors
)
et
)
existent dans
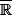
On en déduit que
)
et
)
existent dans
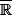
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 15:30
par mehdi-128 » 26 Aoû 2019, 15:30
lyceen95 a écrit:Refaire la démonstration, c'est un bien grand mot.
Recopie la démonstration, en remplaçant les mots 'croissant' par 'décroissant' , 'positif' par 'négatif' , 'plus' par 'moins' ... et voilà.
Le travail de réflexion ne devrait pas être trop compliqué.
Borne supérieure par borne inférieure,

par

etc

-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Aoû 2019, 15:36
par GaBuZoMeu » 26 Aoû 2019, 15:36
Inutile de recopier la démonstration en changeant les mots.
On a montré que si

est croissante sur
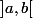
elle a une limite en

et en

(dans la droite achevée.
Si

est décroissante sur
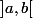
, alors
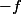
est .... et donc
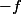
a .... , ce qui prouve que

a ...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 15:41
par mehdi-128 » 26 Aoû 2019, 15:41
Si

est décroissante sur
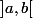
, alors
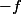
est croissante et donc
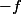
admet une limite , ce qui prouve que

admet une limite.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Aoû 2019, 15:43
par GaBuZoMeu » 26 Aoû 2019, 15:43
limite en

et en

.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 16:09
par mehdi-128 » 26 Aoû 2019, 16:09
Ok merci !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 16:18
par mehdi-128 » 26 Aoû 2019, 16:18
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Aoû 2019, 17:46
par mehdi-128 » 26 Aoû 2019, 17:46
mehdi-128 a écrit:Bonjour,
Soit  une fonction monotone définie sur un intervalle ouvert
une fonction monotone définie sur un intervalle ouvert 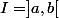 avec
avec  \in \bar \R^2) et
et 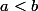 . Alors
. Alors ) et
et ) existent dans
existent dans 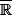
La démonstration est réalisée pour le cas

croissante et l'auteur précise : "on peut supposer sans perte de généralité que

est croissante."
Je ne comprends pas pourquoi on n'a pas besoin de refaire la démonstration pour

décroissante. Comment l'adapter rapidement pour ne pas tout refaire ?
La démonstration part du cas
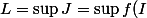)
majorée.
Soit
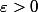
, par définition de la borne supérieure il existe un réel
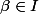
tel que
 \geq L- \varepsilon)
. D'après la croissance de

, pour
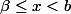
on a :
 \leq f(x) \leq L \leq L+\varepsilon)
Par définition de la limite
 = L)
Je ne comprends pas un passage dans la suite :
Soit
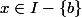
. Puisque

est croissante, on a pour tout
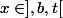
:
 \leq f(t) \leq f_{]x,b[}(t))
.
Puisque la fonction est croissante et minorée par ) d'après la démonstration ci-haut, la fonction
d'après la démonstration ci-haut, la fonction 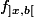 admet une limite finie en
admet une limite finie en  .
.En quoi la démonstration ci haut justifie que
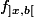
admet une limite finie en

?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 01:41
par mehdi-128 » 27 Aoû 2019, 01:41
Quelqu'un pourrait m'aider ?

Ceci est la démonstration du résultat suivant :
Soit

une fonction croissante définie sur un intervalle

d'extrémités

dans
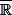
alors pour tout
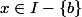
la fonction

a une limite à droite en

et
 \leq f(x^+))
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 27 Aoû 2019, 07:19
par Kolis » 27 Aoû 2019, 07:19
mehdi-128 a écrit: mehdi-128 a écrit:La démonstration part du cas
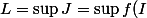)
majorée.
Je ne comprends pas un passage dans la suite :
Soit
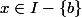
. Puisque

est croissante, on a pour tout
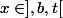
:
 \leq f(t) \leq f_{]x,b[}(t))
.
En quoi la démonstration ci haut justifie que
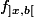
admet une limite finie en

?
Quand on voit ce genre de questions on se demande ce que tu as compris de ce qui a été écrit précédemment ? Ou alors tu as des connaissances insuffisantes pour le comprendre !
Bref on te donne
explicitement un minorant d'un ensemble de réels et tu voudrais savoir pourquoi la borne inférieure est un réel ?
Ou alors tu lis sans réfléchir et n'as pas compris l'importance de
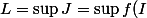)
qui est fondamentale !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 14:34
par mehdi-128 » 27 Aoû 2019, 14:34
Mais à quoi sert le minorant ? Pourquoi vous parlez de borne inférieure est décroissante et non pas croissante ?
Dans la démonstration on a :
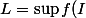= \lim _b f \ \text{si f(I) majore})
et
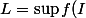 = +\infty \ \text{si f(I) non majore})
Mais ici qu'est ce que j'en sais si
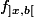
est majorée

Pour avoir une limite finie il faut croissante majorée ou décroissante minorée d'après ce que j'ai vu dans le chapitre précédent sur les suites non ?
On sait juste que :
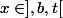
:
 \leq f(t) \leq f_{]x,b[}(t))
.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 27 Aoû 2019, 16:47
par Kolis » 27 Aoû 2019, 16:47
Donc tu sais que
)
minore
)
et
tu as perdu de vue que tu cherches la limite à droite en

(sinon aucune raison de manipuler les
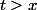
).
Pour les limites à gauche d'une fonction croissante on regarde la borne supérieure, pour les limites à droite c'est différent.
C'est d'ailleurs ce que tu as écrit en toutes lettres dans ton message : "Quelqu'un pourrait m'aider ?" à 00:41
Belle occasion de redire que tu ne lis pas ce que tu écris !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 17:35
par mehdi-128 » 27 Aoû 2019, 17:35
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
une fonction monotone définie sur un intervalle ouvert
avec
et
. Alors
et
existent dans
croissante et l'auteur précise : "on peut supposer sans perte de généralité que
est croissante."
décroissante. Comment l'adapter rapidement pour ne pas tout refaire ?
majorée.
, par définition de la borne supérieure il existe un réel
tel que
. D'après la croissance de
, pour
on a :
majorée.
. Puisque
est croissante, on a pour tout
:
.
admet une limite finie en
?
 Pour avoir une limite finie il faut croissante majorée ou décroissante minorée d'après ce que j'ai vu dans le chapitre précédent sur les suites non ?
Pour avoir une limite finie il faut croissante majorée ou décroissante minorée d'après ce que j'ai vu dans le chapitre précédent sur les suites non ?