Théorème de l'application ouverte

[legeniedesalpages]

Bonsoir,

il y a un point dans la démonstration du théorème de l'application ouverte (dans le Brezis) que j'ai du mal à saisir:

On considère un opérateur linéaire et continu de dans qui vérifie la condition suivante:

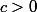
Il existe tel que .

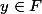
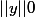
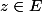
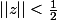
Soit avec , il existe avec et

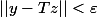
[abcd22]

Bonjour,
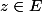
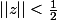
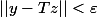
L'hypothèse entraîne , la propriété « pour tout , il existe avec et » est juste la traduction avec des normes de la définition de « y appartient à l'adhérence de T(B(0,1/2)) ».

[legeniedesalpages]

ok, merci abcd22.