Suites réèlles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 23 Sep 2009, 04:56
par Kimou » 23 Sep 2009, 04:56
Bonjour voila un petit exo qui me pose des difficultés.
Soit
)
définie par

et

strictement positifs et
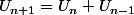
pour
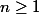
a) Montrer que
)
existe et la determiner. Que remarquez vous?
=> Converge vers 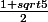
b) Soit


Exprimer

en fonction de
 =>Ici je trouve:
=>Ici je trouve: 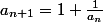
c)Montrer que
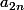
et
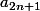
sont adjacentes
d) determiner un rationnel r tel que
 \le10^{-3})
a) J'ai trouver la limite mais je en sais pas dire qu'elle existe.
et c) d) je ne sais pas trop comment m'y prendre.
Merci d'avance!

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 23 Sep 2009, 10:54
par fourize » 23 Sep 2009, 10:54
oh popop !
au passage BONJOUR!
il y a des grosses anbigutés lié à votre façon de presenter
votre suite ! si tu pourrait les rectifiés pour qu'on puisse comprendre la meme chose tous. merci !
* In God we trust, for all others bring data *
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 24 Sep 2009, 09:52
par Kimou » 24 Sep 2009, 09:52
fourize a écrit:oh popop !
au passage BONJOUR!
il y a des grosses anbigutés lié à votre façon de presenter
votre suite ! si tu pourrait les rectifiés pour qu'on puisse comprendre la meme chose tous. merci !
salut!
voila j'ai changé je l'avais tapé très vite avant de partir le matin. Normalement c'est rectifié.
Je vous remercie d'avance.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Sep 2009, 16:34
par girdav » 24 Sep 2009, 16:34
Bonjour.
Que sais-tu sur les suites adjacentes?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 24 Sep 2009, 16:51
par Finrod » 24 Sep 2009, 16:51
Pour a) il faut employer la méthode la plus courante :
étudie la monotonie et les bornes de la suite Un+1/Un. Je veux dire : vérifie qu'elle est bornée.
Pour le reste, il te suffit davoir la définition de suite adjacente.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 09:11
par Kimou » 27 Sep 2009, 09:11
girdav a écrit:Bonjour.
Que sais-tu sur les suites adjacentes?
Bonjour oui je connais la définition des suites adjacentes mais en pratiques, pour montrer que la différence des limites tend vers 0, est ce que je peux dire que

et

tend vers la même limite donc a forciori
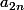
et
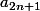
donc leur différence est forcément égale à 0 (étant le memes limites)?
Si non où est l'erreur?
merci
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 09:54
par Kimou » 27 Sep 2009, 09:54
girdav a écrit:Bonjour.
Que sais-tu sur les suites adjacentes?
Bonjour oui je connais la définition des suites adjacentes mais en pratiques, pour montrer que la différence des limites tend vers 0, est ce que je peux dire que

et

tend vers la même limite donc a forciori
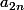
et
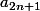
donc leur différence est forcément égale à 0 (étant le memes limites)?
Si non où est l'erreur?
merci
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 12:34
par Kimou » 27 Sep 2009, 12:34
girdav a écrit:Bonjour.
Que sais-tu sur les suites adjacentes?
Bonjour oui je connais la définition des suites adjacentes mais en pratiques, pour montrer que la différence des limites tend vers 0, est ce que je peux dire que

et

tend vers la même limite donc a forciori
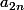
et
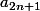
donc leur différence est forcément égale à 0 (étant le memes limites)?
Si non où est l'erreur?
En gros puis-je affirmer:

et

tendent vers

alors forcément

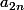
et
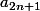
tendent aussi vers

(par récurrence)?
merci
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 15:33
par Kimou » 27 Sep 2009, 15:33
En gros puis-je affirmer:

et

tendent vers

alors forcément

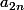
et
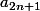
tendent aussi vers

(par récurrence)?
merci
Personne svp?
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 16:59
par Kimou » 27 Sep 2009, 16:59
En gros puis-je affirmer:

et

tendent vers

alors forcément

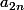
et
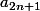
tendent aussi vers

(par récurrence)?
merci
Personne svp?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Sep 2009, 17:01
par girdav » 27 Sep 2009, 17:01
C'est vrai grâce aux résultats sur les sous-suites.
Mais je crois qu'il faut vérifier les "conditions d'adjacence", c'est-à-dire
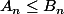
,
)
croissante,
)
décroissante et la limite de la différence qui est nulle.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 17:11
par Kimou » 27 Sep 2009, 17:11
girdav a écrit:C'est vrai grâce aux résultats sur les sous-suites.
Mais je crois qu'il faut vérifier les "conditions d'adjacence", c'est-à-dire
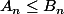
,
)
croissante,
)
décroissante et la limite de la différence qui est nulle.
Merci,
Oui mais on tourne en rond parce que si ce résultat est vrai j'arrive à démontrer que
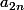
et
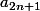
ont une limite commune et donc que leur différence de limite tend vers 0...
Je sais pas si je suis assez clair
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Sep 2009, 17:42
par girdav » 27 Sep 2009, 17:42
Attention j'ai mal lu l'énoncé! Il s'agit de la suite
)
et non de
)
. Je ne sais pas si la suite
)
converge: il faut tout vérifier.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 18:11
par Kimou » 27 Sep 2009, 18:11
girdav a écrit:Attention j'ai mal lu l'énoncé! Il s'agit de la suite
)
et non de
)
. Je ne sais pas si la suite
)
converge: il faut tout vérifier.
Oui c'est vérifié, ainsi que

, d'où ma question, puis- je en conclure que par réccurrence forcement
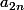
et
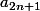
, converge de même manière.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Sep 2009, 18:48
par girdav » 27 Sep 2009, 18:48
Oui, mais la question est bizarre. Puisque tu as montré que la suite converge, le seul intérêt de montrer que les sous-suite d'indice pair et impair sont adjacentes serait l'encadrement de la limite, ce qui permet entre autre de regarder la vitesse de convergence.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 18:58
par Kimou » 27 Sep 2009, 18:58
girdav a écrit:Oui, mais la question est bizarre. Puisque tu as montré que la suite converge, le seul intérêt de montrer que les sous-suite d'indice pair et impair sont adjacentes serait l'encadrement de la limite, ce qui permet entre autre de regarder la vitesse de convergence.
je pense qu'ils nous ont mis les sous suites d'indices pairs et impairs pour répondre à la deuxième partie de la question sur l'adjacence a savoir, la croissance de l'une et la décroissance de l'autre...du moins c'est grace au fait que 2n soit pair et 2n+1 soit impair que j'ai réussie a répondre... :id:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Sep 2009, 19:06
par girdav » 27 Sep 2009, 19:06
C'est ça, en fait on oscille autour de limite, en passant un coup au-dessus et un coup en dessous, le tout avec une amplitude de plus en plus petite.
Tu as réussi la dernière question?
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 19:14
par Kimou » 27 Sep 2009, 19:14
girdav a écrit:C'est ça, en fait on oscille autour de limite, en passant un coup au-dessus et un coup en dessous, le tout avec une amplitude de plus en plus petite.
Tu as réussi la dernière question?
Oui exactement, merci pour ton aide en tout cas!
ben la dernière question il suffit de trouver un r donc j'ai viré les valeurs absolues et j'ai résolu ca me donne un r qui marche...Mais a la réfexion c'est vrai qu'il ne semble pas etre rationnel a cause du racine de 5... je réfléchie a une autre méthode
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Sep 2009, 19:37
par girdav » 27 Sep 2009, 19:37
Petite piste: la suite
)
est une suite de rationnels, qui converge vers
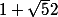
. Regarde quand est-ce que l'écart entre deux termes de la forme
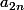
et
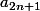
est plus petit que
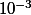
.
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 27 Sep 2009, 19:41
par Kimou » 27 Sep 2009, 19:41
girdav a écrit:Petite piste: la suite
)
est une suite de rationnels, qui converge vers
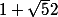
. Regarde quand est-ce que l'écart entre deux termes de la forme
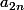
et
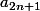
est plus petit que
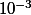
.
On sait que
)
est suite de rationnels?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
,
croissante,
décroissante et la limite de la différence qui est nulle.