Je ne comprends pas cet énoncé; admettons que la première question ait pour but de montre que
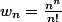
diverge vers +oo; il sufit d'écrire
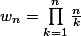
qui est minorée trivialement par

puisque tout les termes du produit son
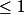
; et c'est donc en fait
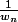
qui converge vers 0.
Ensuite; on s'intéresse à
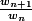
=
^n)
et bizarrement on te demande de montrer que
^n\geq 2)
, ce qui est immédiat en utilisant la formule du binôme de Newton, mais on ne cherche pas la limite qui est pourtant un résultat à connaître.
Alors je ne sais pas quand on te demande de montrer que
=x-ln(1+x)-)
\leq 0)
c'est une étude de fonction classique décroissante et qui vaut 0 en 0; donc je suppose que tu n'as pas vu les développements limités!
Donc ll faut écrire
\geq x-\frac{x^2}{2})
, puis poser
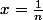
, ce qui done
^n=nln(1+\frac{1}{n})\geq n(\frac{1}{n}-\frac{1}{2n^2}\geq 1-\frac{1}{2n} e)
t on ne peut pas conclure sur la limite de
^n)
qui est

.
Donc si tu n'as aucun outil, la solution que je donne pour

ne sert à rien. Ce problème a été donné en quelle section,si c'est pas indiscret?