Séries entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mike_51
- Membre Naturel
- Messages: 76
- Enregistré le: 14 Nov 2005, 22:50
-
 par Mike_51 » 04 Fév 2006, 18:21
par Mike_51 » 04 Fév 2006, 18:21
Bonjour. Est-ce qu'il y orait unp'tit génie en maths qui pourrait m'aider a faire (ou au moins commencer) cet exo:
On pose Uo=1 et Pour tout n, U(n+1)=UoUn+U1U(n-1)+...+UnUo.
Calculer la somme de n=0 a +oo de Unx^n.
Merci.
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 04 Fév 2006, 18:56
par quinto » 04 Fév 2006, 18:56
Mike_51 a écrit:Bonjour. Est-ce qu'il y orait unp'tit génie en maths qui pourrait m'aider a faire (ou au moins commencer) cet exo:
On pose Uo=1 et Pour tout n, U(n+1)=UoUn+U1U(n-1)+...+UnUo.
Calculer la somme de n=0 a +oo de Unx^n.
Merci.
Bonjour, merci de parler français.
Qu'as tu déjà fait?
-
memphisto
- Membre Relatif
- Messages: 143
- Enregistré le: 18 Jan 2006, 19:17
-
 par memphisto » 04 Fév 2006, 19:03
par memphisto » 04 Fév 2006, 19:03
As tu essayé d'exprimer u_n en fonction de n ?
-
Zeitblom
- Membre Naturel
- Messages: 90
- Enregistré le: 12 Juil 2005, 12:48
-
 par Zeitblom » 04 Fév 2006, 19:24
par Zeitblom » 04 Fév 2006, 19:24
Dans le chapitre Séries entières, un truc qui a cette tête :UoUn+U1U(n-1)+...+UnUo , à quoi pense t-on ? A un produit bien sûr !
Appelle f la somme de ta série, (que tu supposes de rayon non nul) et calcule f(x)^2 par exemple.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Fév 2006, 19:24
par yos » 04 Fév 2006, 19:24
Produit de Cauchy en décomposant aussi x^n en x^k x^(n-k)
-
Mike_51
- Membre Naturel
- Messages: 76
- Enregistré le: 14 Nov 2005, 22:50
-
 par Mike_51 » 04 Fév 2006, 19:56
par Mike_51 » 04 Fév 2006, 19:56
Merci pour les indications. J'avais penser à interpréter cette série comme un produit de Cauchy, mais ce n'est pas pour autant simple. Car ils faut montrer la convergence absolue des 2 séries du produit et on revient (presque) à la série de départ.
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 04 Fév 2006, 20:57
par isortoq » 04 Fév 2006, 20:57
Si f(x) est la somme, f(0)=1 et si le rayon de convergence R est >0, alors pour x non nul on a
xf(x)^2-f(x)+1=0
un petit discriminant et on a f(x) (pour décider entre les 2 racines on utilise la continuité de f en 0)
Mais R est-il >0 ??
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Fév 2006, 21:28
par yos » 04 Fév 2006, 21:28
Donc, selon isortogonal, f(x)=2/[1+racine(1-4x)]
Qui se développe en série entière avec assurément R=1/4.
Ca devrait permettre de conclure, non?
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 04 Fév 2006, 22:26
par isortoq » 04 Fév 2006, 22:26
What you mean Yos ? M'aurais-je gouré ??
-
memphisto
- Membre Relatif
- Messages: 143
- Enregistré le: 18 Jan 2006, 19:17
-
 par memphisto » 04 Fév 2006, 22:33
par memphisto » 04 Fév 2006, 22:33
lol^^mdr^^
me serais-je gouré?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Fév 2006, 22:51
par yos » 04 Fév 2006, 22:51
Non mon argument est faiblard. Ce que j'espèrais, c'est qu'en développant
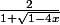
on arrive à des coef

explicites, et on pourrait trouver le rayon de convergence avec ça. J'ai pas trop essayé, j'ai plutôt tenté de majorer

, mais c'est pas évident. Les termes montent vite et ça m'étonnerait pas trop que R=0.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Fév 2006, 23:43
par yos » 04 Fév 2006, 23:43
Ah si ça marche. On trouve
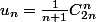
Et c'est bien R=1/4.
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 05 Fév 2006, 09:18
par isortoq » 05 Fév 2006, 09:18
Hum !... j'avais failli écrire : "M'aurais-je gouru ?"... J'ai bien fait de me retenir, car Memphisto veille...
Sinon, bien vu l'expression de Un... Récurrence ?
-
Mike_51
- Membre Naturel
- Messages: 76
- Enregistré le: 14 Nov 2005, 22:50
-
 par Mike_51 » 05 Fév 2006, 14:30
par Mike_51 » 05 Fév 2006, 14:30
Hello! J'ai un peu (peut-etre trop?) de mal à comprendre comment vous résolvez l'équation du 2nd degré, puisque les coefficients ne sont pas constant, à cause du x devant f(x)?
-
memphisto
- Membre Relatif
- Messages: 143
- Enregistré le: 18 Jan 2006, 19:17
-
 par memphisto » 05 Fév 2006, 14:30
par memphisto » 05 Fév 2006, 14:30
Qu' ouis-je? Qu'entends-je? T'aurais tu gouru? ^^
-
memphisto
- Membre Relatif
- Messages: 143
- Enregistré le: 18 Jan 2006, 19:17
-
 par memphisto » 05 Fév 2006, 14:32
par memphisto » 05 Fév 2006, 14:32
Je n'ai pas fais l'exo pour vérifier, Mike_51, mais il faut prendre le x comme un coefficient de l'équation du second degré, dont une des solutions est la fonction f(x). Donc cette solution dépend de x de la même manière que les solutions d'une équation du second degré dépend des coefficients de cette équation.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Fév 2006, 17:33
par yos » 05 Fév 2006, 17:33
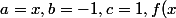=\frac{1-\sqrt{1-4x}}{2x}=\frac{2}{1+\sqrt{1-4x}})
.
La seconde expression est plus lisible en 0 mais la seconde est plus simple pour le DSE.
Appendice culturel :

est le n-ème nombre de Catalan. C'est le nombre de valeurs différentes que peut prendre un produit
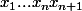
lorsque la loi n'est pas associative.
-
Mike_51
- Membre Naturel
- Messages: 76
- Enregistré le: 14 Nov 2005, 22:50
-
 par Mike_51 » 05 Fév 2006, 18:01
par Mike_51 » 05 Fév 2006, 18:01
Ah oui d'accord merci, j'avais juste pas compris pourquoi le 2 se retoruvait en haut et la racine en bas et j'avais pas penser a multiplier par la quantité conjuguée. Et bravo pour l'appendicite culturelle.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
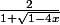 on arrive à des coef
on arrive à des coef  explicites, et on pourrait trouver le rayon de convergence avec ça. J'ai pas trop essayé, j'ai plutôt tenté de majorer
explicites, et on pourrait trouver le rayon de convergence avec ça. J'ai pas trop essayé, j'ai plutôt tenté de majorer  , mais c'est pas évident. Les termes montent vite et ça m'étonnerait pas trop que R=0.
, mais c'est pas évident. Les termes montent vite et ça m'étonnerait pas trop que R=0.