Séries entières et équations différentielles

[jero]

bonjour à tous,j'ai un devoir à faire mais je reste un peu bloquée.Mon problème est le suivant:
on me demande de développer (arcsin x)^2 et (log(1+x))^2 et de former pour chacune de ses fonctions une équation différentielle du second ordre dont elles sont solutions
j'ai tout d'abord poser f(x)=(arcsin x)^2
j'ai ensuite calculé f'(x) et f''(x) mais après je ne sais pas trop ce que je dois faire pour répondre à ce problème

[busard_des_roseaux]

Bonjour,

soit

quand on calcule y", on voit apparaitre comme deuxième terme de la somme
la fonction y'.

L'équation différentielle obtenue est extrêment agréable,
avec des polynômes et pas de racine carrée.

Même phénomène pour la (2).


Ces deux fonctions ont des fonctions dérivées algébriques.

[girdav]

Bonjour;
Il y a le même post sur l'île des mathématiques, en deux fois d'ailleurs.
Le calcul des dérivées est le même dans les deux forums.

[jero]

bonjour j'ai trouvé les deux équations différentielles en calculant les dérivées et je trouve (1-x^2)f''(x)=(xf'(x)/2)+2 pour la fonction (arcsin x)^2
et (1+x)^2f''(x)=2-(1+x)f'(x) pour la fonction (log(1+x))^2
ensuite je pose f(x)= série des a(n)x^n
d'où f'(x)=série des na(n)x^(n-1) et f''(x)=série des n(n-1)a(n)x^(n-2)
ensuite je remplace dans chacune des équations différentielles et je dois identifier les coefficients pour chaque degrès de x
par exemple,quand je remplace dans l'équation différentielle concernant la fonction (log(1+x))^2,je trouve en 0:2a(2)=2-a(1)

[jero]

en degré 1 je trouve 4a(2)+6a(3)=-a(1)-2a(2)
en degré 2 je trouve 2a(2)+12a(3)+12a(4)=-2a(2)-3a(3)
je ne trouve pas de relation,je ne sais pas comment terminer cet exercice,qu'elqu'un a-t-il une idée?
merci d'avance

[jero]

je pense qu'au départ je n'ai pas tout à fait bien exprimer mon sujet,en fait le but de cet exercice et de développer (arcsin x)^2 et (log(1+x))^2,en formant pour chacune des fonctions une équation différentielles dont lles sont solutions.
comme je l'ai dit précédemment je suis parvenue à trouver les 2 équations mais comme je l'ai expliqué ci-dessus,je n'arrive pas a ma dépatouiller pour trouver le développement en série entière malgré mon identification des coefficients
merci d'avance pour votre aide

[Pythales]

Pour la 1ère équation, je trouve
avec , et
(sauf erreur)

[jero]

moi j'ai un pb,je ne trouve pas la même équation que toi,j'ai
(1-x^2)y''-xy'/2=2
une fois que j'ai exprimé a(k+2) comment dois-je faire pour exprimer mon développement?

[jero]

en réalité c'est bon, j'ai trouvé cette équation. mais ma question tient toujours.
merci de votre aide!

[jero]

je n'arrive pas non plus à trouver la relation entre les ak pour le log.

[jero]

merci pour ton aide pythales,j'ai réussi à retrouver ce résultat pour la 1ère équation.par contre pour conclure mon développement,me suffit-il simplement de dire que (arcsin x)^2 = série des (a(k+2)(k+1)(k+2)/k^2) x^n?

[jero]

en ce qui concerne la 2ème équation différentielle,j'ai trouvé une relation entre les a(k):
j'obtiens : (k-1)k a(k)=2*(-1)^k-(k-1)^2*a(k-1)
ai-je bon?

[busard_des_roseaux]

bonjour,

la méthode des DSE est simple:

exprimer toutes les séries sous la forme


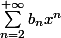
+ quelques termes de début

éventuellement en ayant fait le changement d'indice
n=k-1
ou
n=k-2

une fois trouvée la solution, on peut vérifier qu'elle coïncide
avec le carré d'un DSE (produit de Cauchy = produit de convolution sur
les coefficients)

[Pythales]

En règle générale :
Tu as trouvé une relation de la forme (en décalant l'indice)
Il faut distinguer le cas et
Pour le 1er :


...........................

soit :

en fonction de l'expression de le produit se simplifie presque toujours.
Dans ce cas, la série est .
Même méthode pour

[jero]

je ne comprends pas du tout pourquoi on doit faire cela pythales
de plus je ne comprends pas le raisonnement
je suis complètement perdue !!! peux-tu m'éclaircir un peu plus
as-tu regardé la relation que j'ai trouvé pour les ak de la 2ème équation?est-elle juste cette relation?

[jero]

je suis entrain de regarder la relation que tu m'as donné,si je comprends bien,je dois faire une distingtion de cas car on a une relation entre a(k) et a(k-2)
par contre dans ma relation qui concerne la 2ème équation j'ai une relation entre a(k) et a(k-1) dois-je aussi faire cette distingtion?
par contre je ne vois pas pourquoi tu conclus que (arcsin x)^2= serie de 2 à l'infini a(2p)x^(2p)?
je dois également expliciter la vaeur de a(2p) en fonction de k je suppose?

[jero]

pour le cas k=2p+1
dois-je aller jusqu'à a(3)=f(3)a(1)
soit alors a(2p+1)=f(3)f(5)...f(2p-1)f(2p+1)a(1)

[Pythales]

La réponse est oui à ta dernière question
Pour la 2ème, je trouve effectivement mais si on adopte la méthode précédente, on trouve une relation de récurrence sur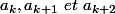
Il vaut mieux écrire l'équation sous la forme et développer 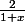en série avant d'identifier.
(et je viens de me rendre compte que ta relation du message #12 est bonne)
Par ailleurs, n'oublie pas que les fonctions dont tu cherches le développement en SE sont une des solutions des équations que tu as formées, puisque tu sais que ces équations admettent deux solutions linéairement indépendantes.

[fourize]

bonjour Jero!

trois à ... posts pour repondre à une seule personne :doh:
comme ça tu sature le forum !!!!!!!

PS. je te lirai plus tard dans la soirée pour rigoler lol

[jero]

pour la relation (k-1)ka(k)=(-1)^n*2-(k-1)^2a(k-1)
dois-je aussi distinguer les cas k=2p et k=2p+1?
et pour conclure l'exercice je n'ai simplement qu'à dire que la série est série des a(2p)x^(2p) ( de même avec a(2p+1))? en explicitant a(2p)?