Series entieres, equations differentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
SamAz
- Membre Naturel
- Messages: 55
- Enregistré le: 29 Jan 2021, 12:54
-
 par SamAz » 26 Sep 2022, 12:24
par SamAz » 26 Sep 2022, 12:24
Bonjours les amis,
j'essaie de resoudre une equation differentielle en utilisant les series entieres et j'aimerais savoir si ma demarche est correcte jusqu'a l'instant ou non
mon equation est:
y''+6xy'+4y=-4)
donc je pose


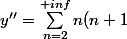C_nx^n-2})
en replacant dans l'equation et ramenant tout en des sommes de qqchose qui multiplie un certain x^k,
je tombe sur des termes qui sortent des sommes, certains sont des constantes et quelque termes sont des constantes qui multiplient x. est-ce normal? en general dans les exercices, les termes qu'ont fait sortir des sommes sont une ou deux des premier termes de la somme mais on tombe seulement sur des constantes et non des termes en x.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Sep 2022, 15:13
par GaBuZoMeu » 26 Sep 2022, 15:13
Bonjour,
Tu as laissé tomber une partie des exposants dans ta formule (mettre les exposants entre accolades si on ne veut pas que ça arrive) et tu n'es trompé pour la dérivée seconde.
Je ne comprends pas ce que tu écris après, donne les résultats que tu trouves et on y verra plus clair.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 26 Sep 2022, 16:30
par tournesol » 26 Sep 2022, 16:30
En général si c'est un terme , c'est une constante et si c'est deux termes , il y a aussi un terme en x.
Et c'est normal.
Si tu as mis sous la forme somme=0,les coefs des termes sortis sont nuls ce qui rend calculables les premiers termes de la série solution.
La nullité des autres coef te donne une relation de recurrence entre les autres, et initialisée par les valeurs déja calculées.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
