Un regard sur la conjecture de Collatz
76 messages
- Page 1 sur 4 - 1, 2, 3, 4
un regard sur la conjecture de Collatz
La conjecture de Collatz est que toute suite de Collatz atteint 1.
On part d'un nombre entier positif quelconque x(1), la suite de Collatz est définie par les deux règles:
1- si le nombre est pair le nombre suivant x(i+1) = x(i)/2
2- si le nombre est impair le nombre suivant x(i+1)=3*x(i)+1
Tout nombre d'une suite de Collatz ne dépend que de son prédécesseur.
En fait la règle 1- devrai s'écrire si le nombre est pair de la forme (2*n+1)*2^k on divise le nombre pair (2*n+1)*2^k par 2^k, ainsi tout nombre pair a un successeur unique impair et tout nombre impair a un successeur unique pair.
Il en découle que tout nombre impair a un descendant impair unique mais peut avoir une infinité d'ascendants impairs.
Une suite de Collatz ne peut pas avoir qu'un seul descendant impair multiple de trois et ce descendant est le résultat de la division de 3*(2*n+1)*2^k par 2^k.
Pour démontrer la conjecture de Collatz supposons le problème résolu, toute suite de Collatz se termine par 1, si il est possible partant de 1 de définir toute suite inverse de Collatz qui peut atteindre tout nombre impair quelconque la démonstration est faite.
Construisons la table T(L,C), L pour ligne et C pour colonne de la façon suivante:
1- La première colonne T(L,1) contient tous les nombres impairs non multiple de 3 dans l'ordre croissant soit T(L,1)=3*L-2 si L impair T(L,1)=3*L-1 si L pair
2- Les colonnes suivantes T(L,C) pour C>1 contiennent tous les prédécesseurs direct possibles de T(L,1) d'une suite de Collatz dans l'ordre croissant.
Pour L impair, C>1, T(L,C) sera égal à ((3*L-2)*4 ^(C-1)-1)/3.
Pour L pair C>1, T(L,C) sera égal à ((6*L-2)*4^(C-2)-1)/3.
On a donc construit une table qui contient dans sa première colonne T(L,1) tout nombre impair non divisible par 3, une fois et une fois seulement dans l'ordre croisant jusqu'à L infini.
Les colonnes T(L,C) pour C de 2 à l'infini contiennent tout nombre impair une fois et une fois seulement pour C de 2 à l'infini.
Si on veut tracer une trajectoire inverse d'une suite de Collatz commençant par 1, le pénultième nombre d'une suite de Collatz sera égal à (4^n-1)/3, n>1 et non multiple de 3 car si n est multiple de 3, (4^n-1)/3 sera multiple de 3 et il n'y aura plus d'ascendant impair.
Si (4^(C-1)-1)/3 n'est pas multiple de 3 c'est un nombre impair présent une fois et une fois seulement colonne T(L,C) et L peut être calculé avec X = (4^n-1)/3,
1- si X de la forme 3*n-1 on déduit L=n et l'antépénultième ascendant impair sera égal à ((6*L-2)*4^(C-2)-1)/3.
2- si X de la forme 3*n-2 on déduit L=n et l'antépénultième ascendant impair sera égal à
((3*L-2)*4^5C-1)-1)/3.
On peut ensuite poursuivre avec les mêmes règles.
On part d'un nombre entier positif quelconque x(1), la suite de Collatz est définie par les deux règles:
1- si le nombre est pair le nombre suivant x(i+1) = x(i)/2
2- si le nombre est impair le nombre suivant x(i+1)=3*x(i)+1
Tout nombre d'une suite de Collatz ne dépend que de son prédécesseur.
En fait la règle 1- devrai s'écrire si le nombre est pair de la forme (2*n+1)*2^k on divise le nombre pair (2*n+1)*2^k par 2^k, ainsi tout nombre pair a un successeur unique impair et tout nombre impair a un successeur unique pair.
Il en découle que tout nombre impair a un descendant impair unique mais peut avoir une infinité d'ascendants impairs.
Une suite de Collatz ne peut pas avoir qu'un seul descendant impair multiple de trois et ce descendant est le résultat de la division de 3*(2*n+1)*2^k par 2^k.
Pour démontrer la conjecture de Collatz supposons le problème résolu, toute suite de Collatz se termine par 1, si il est possible partant de 1 de définir toute suite inverse de Collatz qui peut atteindre tout nombre impair quelconque la démonstration est faite.
Construisons la table T(L,C), L pour ligne et C pour colonne de la façon suivante:
1- La première colonne T(L,1) contient tous les nombres impairs non multiple de 3 dans l'ordre croissant soit T(L,1)=3*L-2 si L impair T(L,1)=3*L-1 si L pair
2- Les colonnes suivantes T(L,C) pour C>1 contiennent tous les prédécesseurs direct possibles de T(L,1) d'une suite de Collatz dans l'ordre croissant.
Pour L impair, C>1, T(L,C) sera égal à ((3*L-2)*4 ^(C-1)-1)/3.
Pour L pair C>1, T(L,C) sera égal à ((6*L-2)*4^(C-2)-1)/3.
On a donc construit une table qui contient dans sa première colonne T(L,1) tout nombre impair non divisible par 3, une fois et une fois seulement dans l'ordre croisant jusqu'à L infini.
Les colonnes T(L,C) pour C de 2 à l'infini contiennent tout nombre impair une fois et une fois seulement pour C de 2 à l'infini.
Si on veut tracer une trajectoire inverse d'une suite de Collatz commençant par 1, le pénultième nombre d'une suite de Collatz sera égal à (4^n-1)/3, n>1 et non multiple de 3 car si n est multiple de 3, (4^n-1)/3 sera multiple de 3 et il n'y aura plus d'ascendant impair.
Si (4^(C-1)-1)/3 n'est pas multiple de 3 c'est un nombre impair présent une fois et une fois seulement colonne T(L,C) et L peut être calculé avec X = (4^n-1)/3,
1- si X de la forme 3*n-1 on déduit L=n et l'antépénultième ascendant impair sera égal à ((6*L-2)*4^(C-2)-1)/3.
2- si X de la forme 3*n-2 on déduit L=n et l'antépénultième ascendant impair sera égal à
((3*L-2)*4^5C-1)-1)/3.
On peut ensuite poursuivre avec les mêmes règles.
Re: un regard sur la conjecture de Collatz
Oui, on peut, mais à l'infini....
Modulo 2^n, il y a en effet un nombre de valeurs résiduelles à étudier.
Inconvénient : si, en proportion de 2^n, la part de ces résiduels diminue, en absolu, elle augmente. Et donc, rien de concluant à attendre pour cette piste.
Modulo 2^n, il y a en effet un nombre de valeurs résiduelles à étudier.
Inconvénient : si, en proportion de 2^n, la part de ces résiduels diminue, en absolu, elle augmente. Et donc, rien de concluant à attendre pour cette piste.
Re: un regard sur la conjecture de Collatz
Conjecture de Collatz ou de Syracuse ou d'Ullam ou conjecture tchèque ou problème 3x+1
Re: un regard sur la conjecture de Collatz
Oui, on peut, mais à l'infini....
Modulo 2^n, il y a en effet un nombre de valeurs résiduelles à étudier.
Inconvénient : si, en proportion de 2^n, la part de ces résiduels diminue, en absolu, elle augmente. Et donc, rien de concluant à attendre pour cette piste.
C'est quoi ces affirmations péremptoires ?
Savez vous qu'en mathématiques ils existent des façons de raisonner qui permettent de faire la preuve d'une formule valable pour n de n=1 à l'infini?
Une des méthode est le raisonnement par récurrence, si on montre que l'affirmation est vraie pour n= 1 to 3 il suffit de démontrer que si elle est vraie pour n+1 qu'elle est aussi vraie pour n, et alors si c'est vérifié elle est vraie pour n infini.
S'il vous plait soyez plus précis dans vos écrits et apportez des arguments pertinents et démontrés à vos affirmations qui pour l'instant restent sans aucune explication ni aucun fondement.
Modulo 2^n, il y a en effet un nombre de valeurs résiduelles à étudier.
Inconvénient : si, en proportion de 2^n, la part de ces résiduels diminue, en absolu, elle augmente. Et donc, rien de concluant à attendre pour cette piste.
C'est quoi ces affirmations péremptoires ?
Savez vous qu'en mathématiques ils existent des façons de raisonner qui permettent de faire la preuve d'une formule valable pour n de n=1 à l'infini?
Une des méthode est le raisonnement par récurrence, si on montre que l'affirmation est vraie pour n= 1 to 3 il suffit de démontrer que si elle est vraie pour n+1 qu'elle est aussi vraie pour n, et alors si c'est vérifié elle est vraie pour n infini.
S'il vous plait soyez plus précis dans vos écrits et apportez des arguments pertinents et démontrés à vos affirmations qui pour l'instant restent sans aucune explication ni aucun fondement.
Re: un regard sur la conjecture de Collatz
Bonjour
La suite de Syracuse est appelée "3x+1 problem" dans la littérature. Il y a très peu de résultats concernant ce problème, l'approche est le plus souvent probabiliste. Les chercheurs se détournent de ce problème, les difficultés étant immenses.
La suite de Syracuse est appelée "3x+1 problem" dans la littérature. Il y a très peu de résultats concernant ce problème, l'approche est le plus souvent probabiliste. Les chercheurs se détournent de ce problème, les difficultés étant immenses.
Re: un regard sur la conjecture de Collatz
Il n'est pas nécessaire d'espérer pour entreprendre ni de réussir pour persévérer ( Guillaume d'Orange ).
Il n'y a pas de difficultés, il n'y a que des ignorants qui en ont peur des difficultés ou qui sont incompétent, quand Erdös a dit les mathématiques ne sont pas prêtes pour de tels problèmes il était au 20ème siècle il y-a 80 ans passés et les moyens de calcul actuels n'existaient pas.
Il faut travailler quelques mois sur la conjecture de Collatz pour comprendre le problème posé, ce que j'ai fait et il ne cessent de se trouver des incompétents qui n'ont jamais fait le même travail mais qui s'empressent de le dénigrer sans rien y comprendre et sans même essayer de le comprendre!
J'ai du mal à croire qu'il y-a autant d'hommes irresponsables ou d'ignorants ou instruits mais incompétents sur cette terre et incapables de lire et de comprendre ce qui a demandé des mois de recherches et de calculs avant d'exprimer le résultat de ses travaux.
Monsieur "l'aviateur" bon vol mais attention vous risquez de tomber de trop haut, pour votre sécurité je vous conseille le parachute!
Les difficultés ne sont immenses que pour ceux qui les contournent, impossible n'est pas Français et Français je suis !
Il n'y a pas de difficultés, il n'y a que des ignorants qui en ont peur des difficultés ou qui sont incompétent, quand Erdös a dit les mathématiques ne sont pas prêtes pour de tels problèmes il était au 20ème siècle il y-a 80 ans passés et les moyens de calcul actuels n'existaient pas.
Il faut travailler quelques mois sur la conjecture de Collatz pour comprendre le problème posé, ce que j'ai fait et il ne cessent de se trouver des incompétents qui n'ont jamais fait le même travail mais qui s'empressent de le dénigrer sans rien y comprendre et sans même essayer de le comprendre!
J'ai du mal à croire qu'il y-a autant d'hommes irresponsables ou d'ignorants ou instruits mais incompétents sur cette terre et incapables de lire et de comprendre ce qui a demandé des mois de recherches et de calculs avant d'exprimer le résultat de ses travaux.
Monsieur "l'aviateur" bon vol mais attention vous risquez de tomber de trop haut, pour votre sécurité je vous conseille le parachute!
Les difficultés ne sont immenses que pour ceux qui les contournent, impossible n'est pas Français et Français je suis !
Re: un regard sur la conjecture de Collatz
Bonjour. Quelle agressivité! Je ne vois pas ce que j'ai dit de mal et rien ne t'empêche de chercher. Je n'ai simplement fait que remarquer que c'est un problème qui n'avance pas vu les difficultés. Je n'ai absolument rien dénigré. C'est un peu scandaleux la façon dont tu me parles.
Maintenant des zozos qui pensent faire avancer les choses, sans jamais arriver à faire publier le moindre résultat (puisqu'il n'y en a pas), je peux te rassurer il y en beaucoup dans le monde et pas seulement en mathématiques (en médecine je connais un cas concret qui au demeurant n'a aucune formation médicale) .
Alors soit modeste, cherche, trouve (si possible) et publie.
Maintenant des zozos qui pensent faire avancer les choses, sans jamais arriver à faire publier le moindre résultat (puisqu'il n'y en a pas), je peux te rassurer il y en beaucoup dans le monde et pas seulement en mathématiques (en médecine je connais un cas concret qui au demeurant n'a aucune formation médicale) .
Alors soit modeste, cherche, trouve (si possible) et publie.
Modifié en dernier par aviateur le 03 Aoû 2018, 22:43, modifié 2 fois.
Re: un regard sur la conjecture de Collatz
Salut,
Si, si, je te jure que ça existe des personnes comme ça. Incroyable, non ?
Bref, tu doit être au bas mot les 127 375 em péquin (*) à penser avoir découvert la lune concernant la conjecture en question et au moins les 10 000em à ne pas être capable de comprendre que certains ont déjà (beaucoup) réfléchi au problème, y compris bien évidement dans cette voie "évidente" consistant à regarder les modulo.
(*) Dans la petite fac où je suis, des "papier" d'amateur pensant avoir découvert la lune concernant syracuse, ben on en reçoit 2 à 3 par ans, tous avec à peu prés le même contenu sans le moindre intérêt (je m'en suis déjà farci plusieurs à feuilleter). Et des utilisant comme toi des congruence; on va dire que c'est de l'ordre de 75%...
C'est pas faux, et j'en connais même des capable d'affirmer que certaines personnes n'ont pas fait un certain travail sans même connaître les sudistes personnes. Et tient toi bien, je connais même un type capable de traiter d'incompétents des personnes sans avoir le début de la moindre idée du travail qu'elles ont fait.CAMI a écrit:Il faut travailler quelques mois sur la conjecture de Collatz pour comprendre le problème posé, ce que j'ai fait et il ne cessent de se trouver des incompétents qui n'ont jamais fait le même travail mais qui s'empressent de le dénigrer sans rien y comprendre et sans même essayer de le comprendre !
Si, si, je te jure que ça existe des personnes comme ça. Incroyable, non ?
Bref, tu doit être au bas mot les 127 375 em péquin (*) à penser avoir découvert la lune concernant la conjecture en question et au moins les 10 000em à ne pas être capable de comprendre que certains ont déjà (beaucoup) réfléchi au problème, y compris bien évidement dans cette voie "évidente" consistant à regarder les modulo.
(*) Dans la petite fac où je suis, des "papier" d'amateur pensant avoir découvert la lune concernant syracuse, ben on en reçoit 2 à 3 par ans, tous avec à peu prés le même contenu sans le moindre intérêt (je m'en suis déjà farci plusieurs à feuilleter). Et des utilisant comme toi des congruence; on va dire que c'est de l'ordre de 75%...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un regard sur la conjecture de Collatz
Et concernant ça :
C'est comme le reste, ça serait pas con de se renseigner un minimum avant d'affirmer de telles conneries : les "moyens de calculs actuels" sont certes bien plus important qu'il y a 80 ans, mais quand on connaît un tant soit peu la nature du problème, ben on sait qu'ils ne sont d'aucune utilité. Je vais t'en apprendre (de nouveau) une bien bonne, mais un ordinateur, avant de lui faire faire des calculs, ben faut un tout petit peu se poser la question de savoir quels calculs on va lui donner à faire.CAMI a écrit:. . .quand Erdös a dit les mathématiques ne sont pas prêtes pour de tels problèmes il était au 20ème siècle il y-a 80 ans passés et les moyens de calcul actuels n'existaient pas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un regard sur la conjecture de Collatz
Bonjour cher ami @CAMI
Quand je dis qu'il n'y a pas beaucoup de résultats, il y en a tout de même mais on est encore très loin de la preuve de la conjecture. Voici quelques références (liste qui n'est pas exhaustive) que tu pourrais lire avant tout.
En effet on ne s'attaque pas à l'Himalaya en short et à pieds nus.
[1] J.C. Lagarias, The 3x + 1 problem and its generalizations, Amer. Math. Monthly 92 (1985),
1{23. MR 86i:11043
[2] R. Terras, A stopping time problem on the positive integers, Acta Arith. 30 (1976), 241{252.
MR 58:27879
[3] G. Wirsching, The Dynamical System Generated by the 3n + 1 Function, Lecture Notes in
Mathematics 1681, Springer-Verlag, Berlin, 1998. MR 99g:11027
[1] D. Applegate and J. C. Lagarias, Density bounds for the 3x + 1 problem I. Tree-search
method, Math. Comp. 64 (1995), 411{426. MR 95c:11024
[2] , Density bounds for the 3x + 1 problem II. Krasikov inequalities, Math. Comp. 64
(1995), 427{438. MR 95c:11025
[3] , The distribution of 3x + 1 trees, Experimental Math. 4 (1995), 101{117. MR
97e:11033
[4] K. Borovkov and D. Pfeifer, Estimates for the Syracuse problem via a probabilistic model,
Theory Probab. Appl. 45 (2000), 300{310.
[5] R. E. Crandall, On the \3x+1" problem, Math. Comp. 32 (1978), 1281{1292. MR 58:494
[6] J. C. Lagarias, The 3x+1 problem and its generalizations, Amer. Math. Monthly 92 (1985),
3{23. MR 86i:11043
[7] J. C. Lagarias and A. Weiss, The 3x + 1 problem: Two stochastic models, Ann. Applied
Prob. 2 (1992), 229{261. MR 92k:60159
[8] H. Muller, Das `3n+1' Problem, Mitteilungen der Math. Ges. Hamburg 12 (1991), 231{251.
MR 93c:11053
[9] T. Oliveira e Silva, Maximum excursion and stopping time record-holders for the 3x + 1
problem: computational results, Math. Comp. 68, No. 1 (1999), 371{384. MR 2000g:11015
[10] D. W. Rawsthorne, Imitation of an iteration, Math. Mag. 58 (1985), 172{176. MR
86i:40001
[11] E. Roosendaal, private communication. See also: On the 3x + 1 problem, electronic manuscript,
available at http://personal.computrain.nl/eric/wondrous
[12] S. Wagon, The Collatz problem, Math. Intelligencer 7 (1985), 72{76. MR 86d:11103
[13] G. J. Wirsching, The dynamical system generated by the 3n + 1 function, Lecture Notes in
Math. No. 1681, Springer-Verlag: Berlin 1998. MR 99g:11027
Quand je dis qu'il n'y a pas beaucoup de résultats, il y en a tout de même mais on est encore très loin de la preuve de la conjecture. Voici quelques références (liste qui n'est pas exhaustive) que tu pourrais lire avant tout.
En effet on ne s'attaque pas à l'Himalaya en short et à pieds nus.
[1] J.C. Lagarias, The 3x + 1 problem and its generalizations, Amer. Math. Monthly 92 (1985),
1{23. MR 86i:11043
[2] R. Terras, A stopping time problem on the positive integers, Acta Arith. 30 (1976), 241{252.
MR 58:27879
[3] G. Wirsching, The Dynamical System Generated by the 3n + 1 Function, Lecture Notes in
Mathematics 1681, Springer-Verlag, Berlin, 1998. MR 99g:11027
[1] D. Applegate and J. C. Lagarias, Density bounds for the 3x + 1 problem I. Tree-search
method, Math. Comp. 64 (1995), 411{426. MR 95c:11024
[2] , Density bounds for the 3x + 1 problem II. Krasikov inequalities, Math. Comp. 64
(1995), 427{438. MR 95c:11025
[3] , The distribution of 3x + 1 trees, Experimental Math. 4 (1995), 101{117. MR
97e:11033
[4] K. Borovkov and D. Pfeifer, Estimates for the Syracuse problem via a probabilistic model,
Theory Probab. Appl. 45 (2000), 300{310.
[5] R. E. Crandall, On the \3x+1" problem, Math. Comp. 32 (1978), 1281{1292. MR 58:494
[6] J. C. Lagarias, The 3x+1 problem and its generalizations, Amer. Math. Monthly 92 (1985),
3{23. MR 86i:11043
[7] J. C. Lagarias and A. Weiss, The 3x + 1 problem: Two stochastic models, Ann. Applied
Prob. 2 (1992), 229{261. MR 92k:60159
[8] H. Muller, Das `3n+1' Problem, Mitteilungen der Math. Ges. Hamburg 12 (1991), 231{251.
MR 93c:11053
[9] T. Oliveira e Silva, Maximum excursion and stopping time record-holders for the 3x + 1
problem: computational results, Math. Comp. 68, No. 1 (1999), 371{384. MR 2000g:11015
[10] D. W. Rawsthorne, Imitation of an iteration, Math. Mag. 58 (1985), 172{176. MR
86i:40001
[11] E. Roosendaal, private communication. See also: On the 3x + 1 problem, electronic manuscript,
available at http://personal.computrain.nl/eric/wondrous
[12] S. Wagon, The Collatz problem, Math. Intelligencer 7 (1985), 72{76. MR 86d:11103
[13] G. J. Wirsching, The dynamical system generated by the 3n + 1 function, Lecture Notes in
Math. No. 1681, Springer-Verlag: Berlin 1998. MR 99g:11027
Re: un regard sur la conjecture de Collatz
C'est un classique d’algorithmique aussi : trouver l'altitude et la durée de vol pour chaque nombre entier
Re: un regard sur la conjecture de Collatz
Ce qui est le plus étrange c'est qu'aucun des commentaires ne dit mot sur mon écrit concernant les fautes éventuelles de résultats mathématiques facile à vérifier.
J'en déduit que rien n'est faux dans mes propositions sinon j'aurai eu quelques remarques sur mes erreurs, j'ai au moins cette consolation.
J'en déduit que rien n'est faux dans mes propositions sinon j'aurai eu quelques remarques sur mes erreurs, j'ai au moins cette consolation.
Re: un regard sur la conjecture de Collatz
C'est peut être parce que tu n'as rien écrit d'intéressant ?
Ah, si tu pouvais prouver que, à partir de 1, on peut remonter sur n'importe quel nombre par l'algorithme, je dis pas, on regarderait ça de près....
Ah, si tu pouvais prouver que, à partir de 1, on peut remonter sur n'importe quel nombre par l'algorithme, je dis pas, on regarderait ça de près....
Re: un regard sur la conjecture de Collatz
Ceci dit,
Voici une erreur que j'ai relevé :
Je passe sur le lapsus qui a inversé et
et  ; mais le raisonnement par récurrence ne dit pas que c'est vrai pour n infini, mais que c'est vrai pour tout
; mais le raisonnement par récurrence ne dit pas que c'est vrai pour n infini, mais que c'est vrai pour tout 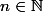 ce qui est totalement différent : notamment parce qu'un entier naturel n'et pas infini par définition même.
ce qui est totalement différent : notamment parce qu'un entier naturel n'et pas infini par définition même.
Ce qui revient à dire : en effectuant un raisonnement par récurrence, si je prouve "qu'à l'infini" j'arrive à un résultat, cela ne veut pas dire que je peux atteindre ce résultat de façon finie.
CAMI a écrit:Ce qui est le plus étrange c'est qu'aucun des commentaires ne dit mot sur mon écrit concernant les fautes éventuelles de résultats mathématiques facile à vérifier.
J'en déduit que rien n'est faux dans mes propositions sinon j'aurai eu quelques remarques sur mes erreurs, j'ai au moins cette consolation.
Voici une erreur que j'ai relevé :
CAMI a écrit:Une des méthode est le raisonnement par récurrence, si on montre que l'affirmation est vraie pour n= 1 to 3 il suffit de démontrer que si elle est vraie pour n+1 qu'elle est aussi vraie pour n, et alors si c'est vérifié elle est vraie pour n infini.
Je passe sur le lapsus qui a inversé
Ce qui revient à dire : en effectuant un raisonnement par récurrence, si je prouve "qu'à l'infini" j'arrive à un résultat, cela ne veut pas dire que je peux atteindre ce résultat de façon finie.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: un regard sur la conjecture de Collatz
Bonjour
Alors là, tu te trompes. Dès que je me mets à lire, déjà je suis un peu perdu.
En effet à la première ligne tu écris:
J'appelle ce genre de phrase une phrase stérile. En effet, une suite du problème 3x+1 n'est malgré tout qu'une suite. Si tu l'appelles) ta suite, dire que le terme
ta suite, dire que le terme  ne dépend que de
ne dépend que de  ! Ben oui mais qu'est que cela veut dire dépendre de son prédécesseur?
! Ben oui mais qu'est que cela veut dire dépendre de son prédécesseur?
Bon maintenant, je me dis va voir plus tu comprendras mieux!
tu comprendras mieux!
Boum, patatrac. Un nombre ne dépend que de son prédécesseur mais peut avoir une infinité d'ascendants.
Donc le prédécesseur est unique pas l'ascendant! Donc prédécesseur et ascendant c'est pas pareil

Après je vais voir plus loin, je lis alors le texte ci-dessous, mais moi là je n'en peux plus .
Personnellement, je pense que si tu veux être compris il faut revoir ton texte, d'autant plus que par la suite
tu n'utilises pas les commandes latex donc c'est indigeste à lire.
CAMI a écrit:Ce qui est le plus étrange c'est qu'aucun des commentaires ne dit mot sur mon écrit concernant les fautes éventuelles de résultats mathématiques facile à vérifier.
J'en déduit que rien n'est faux dans mes propositions sinon j'aurai eu quelques remarques sur mes erreurs, j'ai au moins cette consolation
Alors là, tu te trompes. Dès que je me mets à lire, déjà je suis un peu perdu.
En effet à la première ligne tu écris:
CAMI a écrit:Tout nombre d'une suite de Collatz ne dépend que de son prédécesseur.
J'appelle ce genre de phrase une phrase stérile. En effet, une suite du problème 3x+1 n'est malgré tout qu'une suite. Si tu l'appelles
Bon maintenant, je me dis va voir plus
 tu comprendras mieux!
tu comprendras mieux! CAMI a écrit:Il en découle que tout nombre impair a un descendant impair unique mais peut avoir une infinité d'ascendants impairs.
Boum, patatrac. Un nombre ne dépend que de son prédécesseur mais peut avoir une infinité d'ascendants.
Donc le prédécesseur est unique pas l'ascendant! Donc prédécesseur et ascendant c'est pas pareil

Après je vais voir plus loin, je lis alors le texte ci-dessous, mais moi là je n'en peux plus .
CAMI a écrit:2- Les colonnes suivantes T(L,C) pour C>1 contiennent tous les prédécesseurs direct possibles de T(L,1) d'une suite de Collatz dans l'ordre croissant.
Personnellement, je pense que si tu veux être compris il faut revoir ton texte, d'autant plus que par la suite
tu n'utilises pas les commandes latex donc c'est indigeste à lire.
Re: un regard sur la conjecture de Collatz
les commentaires sont peut être simultanés , ils n'en sont pas pour le moins tous erronés !
J'attend toujours une affirmation précise qui ne soit pas autre chose qu'une contre vérité!
J'attend toujours une affirmation précise qui ne soit pas autre chose qu'une contre vérité!
Re: un regard sur la conjecture de Collatz
Pour être plus précis j'écrit ce qui suit:
La conjecture de Collatz est que toute suite de Collatz atteint 1.
On part d'un nombre entier positif quelconque x(1),
la suite de Collatz est définie par les deux règles:
1- si le nombre est pair le nombre suivant x(i+1) = x(i)/2
2- si le nombre est impair le nombre suivant x(i+1)=3*x(i)+1
Tout nombre d'une suite de Collatz ne dépend que de son prédécesseur.
En fait la règle 1- devrai s'écrire si le nombre est pair de la forme (2*n+1)*2^k on divise le nombre pair (2*n+1)*2^k par 2^k, ainsi tout nombre pair a un successeur unique impair et tout nombre impair a un successeur unique pair.
Il en découle que tout nombre impair a un descendant impair unique mais peut avoir une infinité d'ascendants impairs ou pairs.
Une suite de Collatz ne peut pas avoir qu'un seul descendant impair multiple de trois et ce descendant est le résultat de la division de 3*(2*n+1)*2^k par 2^k, ensuite il ne peut plus exister de descendant impair multiple de 3.
Pour démontrer la conjecture de Collatz supposons le problème résolu, toute suite de Collatz se termine par 1, si il est possible partant de 1 de définir toute suite inverse de Collatz qui peut atteindre tout nombre impair quelconque la démonstration est faite.
Soit 3*n-2 et 3*n-1 tout nombre impair non multiple de 3, n entier positif de 1 à l'infini.
Il est facile de démontrer que tout ascendant impair de 3*n-2 est de la forme:
((3*n-2)*4^k-1)/3 car multiplié par 3 +1 et divisé par 4^k on obtient 3*n-2
Il est facile de démontrer que tout ascendant impair de 3*n-1 est de la forme:
((3*n-1)*2^(2*k-1)-1)/3 car multiplié par 3 +1 et divisé par 2^(2*k-1) on obtient 3*n-2
pour tout nombre entier positif k de 1 à l'infini.
Ce qui est remarquable c'est que pour n entier positif de 1 à l'infini et k entier positif de 1 à l'infini tout nombre impair est représenté une fois et une fois seulement par l'une des 2 équations ((3*n-2)*4^k-1)/3 ou ((3*n-1)*2^(2*k-1)-1)/3 et tout nombre impair non multiple de 3 est représenté une fois et une fois seulement par les équations 3*n-2 ou 3*n-1.
Si on commence une suite inverse de Collatz par 1 les ascendants de 1 sont donnés par l'équation ((3*1-2)*4^k-1)/3.Si k=1 ou si k est multiple de 3 la suite n'a plus d'ascendant impair possible, les ascendants possibles sont pour k>1 et non multiple de 3.
Le pénultième sera donc égal à (4^k-1)/3, k>1 et non multiple de 3, soit les nombres 5, 85, 341, 1365, 5461, 21845 ......, soit x le pénultième nombre choisi, l'antépénultième y sera de la forme (x*4^k-1)/3 si x est de la forme 3*n-2 ou (x*2^(2*k-1)-1)/3 si x est de la forme 3*n-1,
si y est multiple de 3 la suite n'a plus d'ascendant impair, on choisi donc un y non multiple de 3 et ainsi de suite.
Donc une suite inverse se termine par un nombre impair multiple de 3 et diverge vers (3*(2*n+1)*2^k ou diverge vers tout nombre impair infiniment grand multiple de 3 ou non, donc toute suite de Collatz converge vers 1 aussi grand soit le nombre initial choisi.
La conjecture de Collatz est que toute suite de Collatz atteint 1.
On part d'un nombre entier positif quelconque x(1),
la suite de Collatz est définie par les deux règles:
1- si le nombre est pair le nombre suivant x(i+1) = x(i)/2
2- si le nombre est impair le nombre suivant x(i+1)=3*x(i)+1
Tout nombre d'une suite de Collatz ne dépend que de son prédécesseur.
En fait la règle 1- devrai s'écrire si le nombre est pair de la forme (2*n+1)*2^k on divise le nombre pair (2*n+1)*2^k par 2^k, ainsi tout nombre pair a un successeur unique impair et tout nombre impair a un successeur unique pair.
Il en découle que tout nombre impair a un descendant impair unique mais peut avoir une infinité d'ascendants impairs ou pairs.
Une suite de Collatz ne peut pas avoir qu'un seul descendant impair multiple de trois et ce descendant est le résultat de la division de 3*(2*n+1)*2^k par 2^k, ensuite il ne peut plus exister de descendant impair multiple de 3.
Pour démontrer la conjecture de Collatz supposons le problème résolu, toute suite de Collatz se termine par 1, si il est possible partant de 1 de définir toute suite inverse de Collatz qui peut atteindre tout nombre impair quelconque la démonstration est faite.
Soit 3*n-2 et 3*n-1 tout nombre impair non multiple de 3, n entier positif de 1 à l'infini.
Il est facile de démontrer que tout ascendant impair de 3*n-2 est de la forme:
((3*n-2)*4^k-1)/3 car multiplié par 3 +1 et divisé par 4^k on obtient 3*n-2
Il est facile de démontrer que tout ascendant impair de 3*n-1 est de la forme:
((3*n-1)*2^(2*k-1)-1)/3 car multiplié par 3 +1 et divisé par 2^(2*k-1) on obtient 3*n-2
pour tout nombre entier positif k de 1 à l'infini.
Ce qui est remarquable c'est que pour n entier positif de 1 à l'infini et k entier positif de 1 à l'infini tout nombre impair est représenté une fois et une fois seulement par l'une des 2 équations ((3*n-2)*4^k-1)/3 ou ((3*n-1)*2^(2*k-1)-1)/3 et tout nombre impair non multiple de 3 est représenté une fois et une fois seulement par les équations 3*n-2 ou 3*n-1.
Si on commence une suite inverse de Collatz par 1 les ascendants de 1 sont donnés par l'équation ((3*1-2)*4^k-1)/3.Si k=1 ou si k est multiple de 3 la suite n'a plus d'ascendant impair possible, les ascendants possibles sont pour k>1 et non multiple de 3.
Le pénultième sera donc égal à (4^k-1)/3, k>1 et non multiple de 3, soit les nombres 5, 85, 341, 1365, 5461, 21845 ......, soit x le pénultième nombre choisi, l'antépénultième y sera de la forme (x*4^k-1)/3 si x est de la forme 3*n-2 ou (x*2^(2*k-1)-1)/3 si x est de la forme 3*n-1,
si y est multiple de 3 la suite n'a plus d'ascendant impair, on choisi donc un y non multiple de 3 et ainsi de suite.
Donc une suite inverse se termine par un nombre impair multiple de 3 et diverge vers (3*(2*n+1)*2^k ou diverge vers tout nombre impair infiniment grand multiple de 3 ou non, donc toute suite de Collatz converge vers 1 aussi grand soit le nombre initial choisi.
Re: un regard sur la conjecture de Collatz
((3*n-1)*2^(2*k-1)-1)/3 car multiplié par 3 +1 et divisé par 2^(2*k-1) on obtient 3*n-2
pour tout nombre entier positif k de 1 à l'infini.
Le problème est toujours la majoration de la suite
76 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
